Ćwiczenia 3

Powtórzyć: Zasady zachowania pędu, energii mechanicznej i momentu pędu

1. Rozwiąż zagadnienie rzutu ukośnego w polu grawitacyjnym, gdy na poruszające się ciało działa siła oporu proporcjonalna do prędkości. Znaleźć wektory: prędkości
oraz położenia
, wysokość maksymalną oraz czas jej osiągnięcia. Przedyskutować przypadek, gdy siła oporu jest dużo mniejsza od ciężaru ciała.

2. a) Za rozpad promieniotwórczy β odpowiedzialne jest słabe oddziaływanie jądrowe. Np. izotop toru 234 emituje promieniowanie β ^- (elektrony e) pochodzące z rozpadu neutronu n:

, (
- antyneutrino elektronowe, p - proton). Zapisz reakcję rozpadu β ^-dla toru oraz izotopu pierwiastka (jakiego?), który z niego powstaje.

b) Strumień elektronów wyemitowanych podczas rozpadu β ^- kierowany jest w jednorodne pole elektryczne o natężeniu
, panujące w obszarze o szerokości d . Przyjmij, że prędkość początkowa elektronów wynosi
i jest zgodna z kierunkiem
. Po opuszczeniu pola elektrycznego elektrony wchodzą w obszar jednorodnego pola magnetycznego o indukcji
, przy czym
⊥
. Znajdź prędkość elektronów przed wejściem w obszar pola magnetycznego. Znajdź równanie toru elektronów w polu magnetycznym.

0x08 graphic
3. Kula o masie m₁ poruszająca się z prędkością v₁ dogania kulę o masie m₂ poruszającą się z prędkością v₂. Znaleźć szybkość kul po zderzeniu, jeśli jest ono centralne i sprężyste. Rozważ przypadek kul o jednakowych masach oraz przypadek, gdy dodatkowo druga z kula spoczywa.

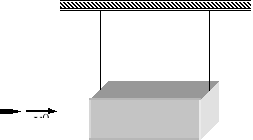
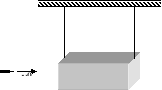
4. Rysunek przedstawia wahadło balistyczne służące do pomiaru prędkości pocisków. Kula o masie m_k wystrzelona poziomo uderza z prędkością v₀ w drewniany blok o masie M. Zderzenie jest całkowicie niesprężyste, a blok wychyla się na wysokość y. Znając wartości: m_k, M, y oblicz prędkość kuli v_0.

5. Po prostoliniowym odcinku toru poruszają się jeden za drugim dwa wagoniki, każdy o masie m i z prędkością
. Zaniedbujemy opory ruchu. Chłopiec o masie m₀ dogania wagonik II i wskakuje na niego, przy czym jego prędkość względem wagonika wynosiła
. a) Czy wartość prędkości w wagonika II wzrośnie czy zmaleje? b) Jeśli wzrośnie i dojdzie do sprężystego zderzenia obu wagoników, to jakie będą ich prędkości w₁ i w₂ po zderzeniu?

6. Atakujący słoń o masie m₁= 5400 kg pędzi w kierunku Jasia-myśliwego z prędkością v₁= 4,30 m/s. Jaś rzuca w jego kierunku piłkę o masie m₂= 0,150 kg, która porusza się z prędkością v₂= 8,11 m/s. a. Ile wyniesie prędkość piłki, gdy po odbiciu od słonia trafi w Jasia? b. Porównaj początkową energię kinetyczną piłki z końcową.

7. Samochód osobowy o masie m₁=950 kg zbliża się do skrzyżowania z prędkością v₁ =16 m/s. Z ulicy prostopadłej wjeżdża na skrzyżowanie z prędkością v₂ =21 m/s minibus o masie m₂=1300 kg i zderza się z samochodem osobowym. Znaleźć wartość prędkości i jej kierunek, jeśli samochody sczepiają się razem w czasie zderzenia, a siły zewnętrzne zaniedbujemy

8. Satelita porusza się wokół Ziemi po orbicie eliptycznej. Kiedy przechodzi przez apogeum, jego odległość od Ziemi wynosi r_a= 24 100 km, a prędkość jest równa v_a= 3990 km/h. W perygeum odpowiednio r_p= 22 500 km i v_p= 4280 km/h. a. Korzystając z tych informacji oblicz masę Ziemi. b. Wykaż, że promień wodzący satelity zakreśla w równych odstępach czasu równe pola (czyli że jego prędkość polowa jest stała, podobnie jak planet poruszających się wokół Słońca).

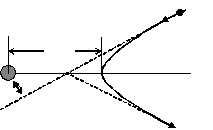
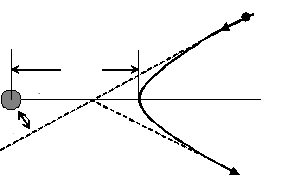
9. Proton zbliża się do nieruchomego jądra atomowego o dużej masie i ładunku +Ze (e - ładunek elementarny, Z - liczba atomowa). W odległości nieskończenie wielkiej prędkość protonu wynosi v₀. Tor ekstrapolowany liniowo od dużych odległości do małych przechodzi przez minimum odległości b od cząstki ciężkiej i odległość ta nosi nazwę parametru zderzenia. Jaka jest odległość największego zbliżenia dla rzeczywistej orbity? Przyjmij, że masa jądra jest tak duża, że można pominąć jego energię odrzutu i jądro pozostaje nieruchome.

10. Rozpatrz ruch wahadła matematycznego o długości l i masie m. Oblicz jego energię kinetyczną i potencjalną dla przypadku małych wychyleń. Sprawdź, czy całkowita energia jest zachowywana. Sporządź wykresy energii kinetycznej i potencjalnej w funkcji czasu.