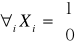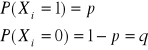Proste regresji drugiego rodzaju:
Def: Prostą ![]()
nazywamy prostą regresji drugiego rodzaju zmiennej Y względem zmiennej X jeżeli ![]()
.
Def: Prostą ![]()
nazywamy prostą regresji drugiego rodzaju zmiennej X względem zmiennej Y jeżeli ![]()
.
![]()
![]()
Równanie prostej regresji II-go rodzaju Y względem X: ![]()
Równanie prostej regresji II-go rodzaju X względem Y: ![]()
![]()
linia regresji drugiego ordzaju zmiennej Y względem X
![]()
![]()
linia regresji drugiego ordzaju zmiennej X względem Y
![]()
CIĄGI ZMIENNYCH LOSOWYCH
![]()
, ![]()
- zmienna losowa
![]()
ciąg zmiennych losowych
Def: Mówimy, że zmienne ![]()
są niezależne jeżeli każdy skonczony podciąg jest niezależny.
Def: Mówimy, że ciąg ![]()
jest stochastycznie zbieżny do zmiennej losowej X (lub zbieżny według prawdopodobieństwa) jeżeli ![]()
![]()
Def: Mówimy, że ciąg ![]()
jest zbieżny do zmiennej losowej X z prawdopodobieństwem równym 1 jeżeli ![]()
![]()
![]()
![]()
![]()
Def: Mówimy, że ciąg ![]()
jest zbieżny do zmiennej losowej X według dystrybuant jeżeli ciąg ![]()
dystrybuant zmiennych ![]()
jest zbieżny do funkcji ![]()
dystrybuanty zmiennej losowej ![]()
w każdym punkcie ciągłości dystrybuanty ![]()
Def: ![]()
![]()
Jeżeli ![]()
to mówimy, że dla ciągu ![]()
zachodzi słebe prawo wielkich liczb.
Tw: Czebyszewa
Jeżeli zmienne ![]()
są niezależne i takie, że ![]()
(wspólnie ograniczone - każda jest mniejsza), to wówczas dla zmiennej ![]()
zachodzi słabe prawo wielkich liczb.
Wniosek: ![]()
o tej samej wariancji , to wówczas z nierówności Czebyszewa 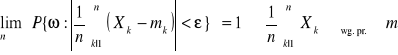
Tw: Lindeberga - Levye'go (globalne twierdzenie graniczne)
![]()
- ciąg zmiennych niezależnych o tych samych rozkładach, tych samych wartościach oczekiwanych ![]()
i warinacjach ![]()
![]()
- nowa zmienna; ![]()
, ![]()
![]()
- standaryzowana zmienna
Teza: Ciąg ![]()
zmieża według dystrybuant do zmiennej losowej ![]()
takiej, że rozkład zmiennej ![]()
jest normalny ![]()
, tzn. ![]()
.
Uwaga: ![]()
zmieżają według dystrybuant do zmiennej ![]()
Def: Jeżeli zachodzi teza twierdzenia Lindeberga - Levye'go, to wówczas mówimy, że zmienna losowa ma rozkład asymptotycznie normalny ![]()
.
Tw: Moivre'a - Laplace'a
|
|
|
![]()
ma rozkład Bernoulliego ![]()
z tw. L-L 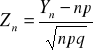
ma rozkład asymptorycznie normalny ![]()
tzn. ![]()
EGZAMIN:
16.06.2001 1130
401,403 A3-A4
3
Luke Rachunek prawdopodobieństwa-wykład 4.6.2k+1
#
Wyszukiwarka
Podobne podstrony:
9221
9221
9221
9221
9221
9221
9221
9221
więcej podobnych podstron