1. Wstęp teoretyczny.

Zgodnie z ISO 1101:1985 na tolerancje geometryczne składają się następujące tole­rancje:

• kształtu (ang. form tolerances),

• kierunku (ang. orientation tolerances),

• położenia (ang. location tolerances),

• bicia (ang. runout tolerances).

Tolerancje kształtu ograniczają tylko odchyłki kształtu elementu rzeczywistego od jego nominalnego odpowiednika. Dlatego są one zaliczane do grupy tolerancji geometrycznych prostych (ang. single geometrical tolerances).

Tolerancje kierunku, położenia i bicia ograniczają zarówno odchyłki kształtu przedmiotu rzeczywistego, jak również odchyłki kierunku lub/i położe­nia. W większości przypadków tolerancje kierunku, położenia i bicia wymagają określenia bazy, dlatego w normie ISO 1101 są one zakwalifikowane jako tolerancje geometryczne względem bazy (ang. geometrical tolerances related to datum).

Do definiowania tolerancji geometrycznych wykorzystuje się geometry­cznie idealne odpowiedniki powierzchni czy linii rzeczywistych. Takimi odpo­wiednikami są element przylegający, element minimalnej strefy (ang. minimum zonę) lub element średni (ang. least sąuare). Przykładami elementów przylega­jących są: prosta i płaszczyzna przylegająca, okrąg przylegający do wałka (ang. minimum circumscribed circle), okrąg przylegający do otworu (ang. maximum inscribed circle), walec przylegający do wałka (ang. minimum circumscribed cylinder) i walec przylegający do otworu (ang. maximum inscribed cylinder).

Najczęściej używanymi w pomiarach wzorcami płaskości są płyty pomiarowe, liniały powierzchniowe i płytki interferencyjne.

Płyty pomiarowe wykonuje się z żeliwa lub granitu. Według [PN-ISO 8512-1, 2] rozróżnia się 4 klasy dokładności płyt pomiarowych oznaczonych (w kolejności malejącej dokładności) symbolami 0, 1, 2 i 3. Tolerancje płaskości całej powierzchni płyt pomiarowych zależą od ich wymiarów i klasy dokładno­ści. Odchyłki płaskości powierzchni cząstkowych o wymiarach 250 mm x 250 mm, położonych w dowolnym miejscu powierzchni roboczej, nie powinny prze­kraczać 3,5; 7; 15 i 30 µm odpowiednio dla płyt klasy dokładności 0, 1, 2 i 3.

Liniały powierzchniowe, podobnie jak płyty pomiarowe, wykonuje się z żeliwa lub granitu. Rozwiązania konstrukcyjne produkowanych w kraju linia­łów podaje [PN-74/M-53180].

W większości przypadków odchyłkę płaskości określa się na podstawie po­miarów wykonanych w pojedynczych punktach powierzchni (pomiary dyskret­ne). Im więcej jest punktów pomiarowych, tym realizacja pomiaru jest bliższa definicji odchyłki. W przypadku powierzchni prostokątnych punkty pomiarowe rozmieszcza się na przekrojach wzdłużnych, poprzecznych i wzdłuż przekąt­nych. Jeżeli pomiary wykonuje się względem powierzchni wzorcowej (wzorzec płaskości), wystarczy mierzyć odchyłki w punktach siatki prostokątnej.

Poziomnice koincydencyjne.

Charakterystyczną cechą tych poziomnic jest możliwość precyzyjnej zmiany położenia ampułki względem korpusu poziomnicy oraz specjalny układ optyczny umożliwiający jednoczesną obserwację obu końców pęcherzyka. Położeniem, w którym odczytuje się wskazanie, jest koincydencja końców pęcherzyka. Zakres pomiarowy poziom­nicy koincydencyjnej firmy Zeiss wynosi ±10 mm/m, z tym że podziałka jest opisana od 0 do 20 mm; położeniu poziomemu odpowiada wskazanie 10 mm/m. Błędy graniczne dopuszczalne w zależności od wykorzystanego zakresu pomia­rowego wynoszą:

• ±0,01 mm/m (±2") — przy wykorzystaniu zakresu ±1 mm/m,

• ±0,02 mm/m (±4") — w całym zakresie.

2. Cel ćwiczenia.

Celem ćwiczenia było zapoznanie się z oznaczeniami tolerancji geometrycznych (tolerancje kształtu, kierunku, położenia i bicia) na rysunku oraz pomiar odchyłki płaskości płyty żeliwnej o wymiarach 500 x 500 z użyciem poziomnicy koincydencyjnej.

3. przebieg ćwiczenia

• Przed przystąpieniem do pomiarów należy sprawdzić czy płyta jest oczyszczona z zabrudzeń i odtłuszczona.

• Na płycie należy nanieść siatkę o skoku równemu rozstawowi osi wałeczków liniału sinusowego o ile nie została ona naniesiona wcześniej.

• Na kolejnych punktach siatki stawiamy liniał sinusowy, a na niego poziomnice

koincydencyjną Następnie dokonujemy odczytu

• Następnym krokiem jest opracowanie wyników, których efektem jest wyznaczenie odchyłki płaskości płyty, którą należy porównać z wartościami dopuszczalnymi zawartymi w PN-ISO 8512 w celu określenia klasy płyty.

• Przed położeniem poziomnicy na sprawdzanej płaszczyźnie, należy pokrętłem nastawczym (bębenkiem) obracać tak, by na skali zgrubnej uzyskać wskazanie „10”, a na skali precyzyjnej wskazanie „0”.

4. Obliczenia.

Wskazania na osi „z” oblicza się według schematu:

z₁ = 0,

z₂ = w_1-2 + z₁,

z₃ = w_2-3 + z₂,

z₄ = w_3-4 + z₃,

itd.

gdzie w_i-j - wskazanie poziomicy

z₁ = 0,

z₂ = w_1-2+ z₁ = -0,836 + 0 = -0,836

z₃ = w_2-3 + z₂ = -0,837 - 0,836 = -1,673

z₄ = w_3-4 + z₃ = -0,836 - 1,673 = -2,509

z₅ = w_4-5 + z₄ = -0,839 - 2,509 = -3,348

z₆ = w_1-6 + z₁ = 0,057 + 0 = 0,057

z₇ = w_6-7 + z₆ = -0,838 + 0,057 = -0,781

z₈ = w_7-8 + z₇ = -0,840 - 0,781 = -1,621

z₉ = w_8-9 + z₈ = -0,840 - 1,621 = -2,461

z₁₀ = w_9-10 + z₉ = -0,840 - 2,461 = -3,301

z₁₁ = w_6-11 + z₆ = 0,044 + 0,057 = 0,101

z₁₂ = w_11-12 + z₁₁ = -0,841 + 0,101 = -0,740

z₁₃ = w_12-13 + z₁₂ = -0,840 - 0,740 = -1,580

z₁₄ = w_13-14 + z₁₃ = -0,841 - 1,580 = -2,421

z₁₅ = w_14-15 + z₁₄ = -0,842 - 2,421 = -3,263

z₁₆ = w_11-16 + z₁₁ = 0,052 + 0,101 = 0,153

z₁₇ = w_16-17 + z₁₆ = -0,841 + 0,153 = -0,688

z₁₈ = w_17-18 + z₁₇ = -0,842 - 0,688 = -1,530

z₁₉ = w_18-19 + z₁₈ = -0,842 - 1,530 = -2,372

z₂₀ = w_19-20 + z₁₉ = -0,840 - 2,372 = -3,212

z₂₁ = w_16-21 + z₁₆ = 0,058 + 0,153 = 0,211

z₂₂ = w_21-22 + z₂₁ = -0,839 + 0,211 = -0,628

z₂₃ = w_22-23 + z₂₂ = -0,840 - 0,628 = -1,468

z₂₄ = w_23-24 + z₂₃ = -0,842 - 1,468 = -2,310

z₂₅ = w_24-25 + z₂₄ = -0,842 - 2,310 = -3,152

KARTA POMIARÓW
Ćw.4. Odchyłki geometryczne, pomiar odchyłki płaskości
1. Odczyt z poziomnicy koincydencyjnej
Rozstaw liniału sinusowego		0.1 m
Punkt Bazowy-mierzony	Wskazanie mm / m	Wskazanie 1mm/liniał (0,1m)	Punkt Bazowy-mierzony	Wskazanie mm / m	Wskazanie 1mm/liniał (0,1m)
1-2	1,638	=(1,638-10)/10= -0,836	16-17	1,584	=(1,584-10)/10= -0,841
2-3	1,623	=(1,623-10)/10= -0,837	17-18	1,580	=(1,580-10)/10= -0,842
3-4	1,621	=(1,621-10)/10= -0,836	18-19	1,580	=(1,580-10)/10= -0,842
4-5	1,610	=(1,610-10)/10= -0,839	19-20	1,591	=(1,591-10)/10= -0,840
6-7	1,616	=(1,616-10)/10= -0,838	21-22	1,606	=(1,606-10)/10= -0,839
7-8	1,600	=(1,600-10)/10= -0,840	22-23	1,592	=(1,592-10)/10= -0,840
8-9	1,598	=(1,598-10)/10= -0,840	23-24	1,572	=(1,572-10)/10= -0,842
9-10	1,591	=(1,591-10)/10= -0,840	24-25	1,588	=(1,588-10)/10= -0,841
11-12	1,590	=(1,590-10)/10= -0,841	1-6	10,570	=(10,570-10)/10= 0 ,057
12-13	1,598	=(1,598-10)/10= -0,840	6-11	10,440	=(10,440-10)/10= 0,044
13-14	1,582	=(1,582-10)/10= -0,841	11-16	10,522	=(10,522-10)/10= 0,052
14-15	1,576	=(1,576-10)/10= -0,842	16-21	10,584	=(10,584-10)/10= 0,058

Odległość punktów mierzonych od płaszczyzny średniej wyznacza się wg wzoru:

Gdzie a, b i c to parametry równania płaszczyzny.

Oblicza się je wg wzoru:

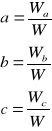
gdzie:

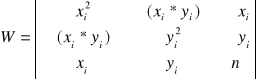
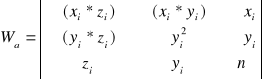
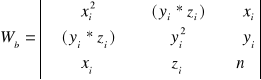
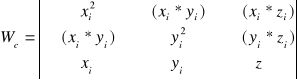
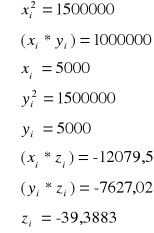
podstawiając wartości, otrzymujemy:

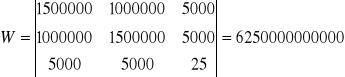
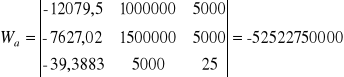
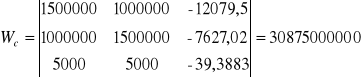
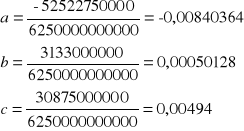
Odchyłka płaskości

Równanie płaszczyzny średniej

z = ax + by +c.

2. Tabela wyników obliczeń
Punkt	Xi	Yi	Zi	di	Punkt	Xi	Yi		Zi	di
1	0	0	0	-0,004939825	14	300	200	-2,421		-0,006103784
2	100	0	-0,836	-0,000775973	15	400	200	-3,263		-0,008139712
3	200	0	-1,673	0,001887933	16	0	300	0,153		-0,002123925
4	300	0	-2,509	0,004351846	17	100	300	-0,688		-0,003359881
5	400	0	-3,348	0,005715797	18	200	300	-1,530		-0,004995823
6	0	100	0,057	0,001931932	19	300	300	-2,372		-0,006631765
7	100	100	-0,781	0,003895862	20	400	300	-3,212		-0,007167746
8	200	100	-1,621	0,004259849	21	0	400	0,211		0,006147782
9	300	100	-2,461	0,004423843	22	100	400	-0,628		0,007111748
10	400	100	-3,301	0,003887862	23	200	400	-1,468		0,006675763
11	0	200	0,101	-0,004195851	24	300	400	-2,310		0,00423985
12	100	200	-0,740	-0,004831829	25	400	400	-3,152		0,003403879
13	200	200	-1,580	-0,004667835
Odchyłka płaskości: d= 0,015251mm.

d_max= 0,007112

d_min= -0,00814

8

---