Fizyka ciała stałego (zakres, definicja) - dzia
ł zajmujący się
ciałami stałymi (w danych warunkach zachowują swój
kształt makroskopowy).
Atomy mogą drgać w swojej sieci krystalicznej
. Jeśli at. Sąu ułożone z pewnymi regułami to są kryształy.
Kwazikryształy - at. Tworzą nieperiodyczną siećo symetrii
5 kątnej. Struktura faz periodyczna lecz gdy
liczba wymiarów
większa od 3. Mogą wykazać np. 5 kątną oś symetrii.
Ciała amorficzne - forma ciała stałego (bezpostaciowa).Własności zbliżone do ciała krystalicznego, cząsteczki
ułożone chaotycznie (podobnie jak w cieczach). Wiązania
natury
chem.
2. Materia - określenie minimum 3 różnych kategorii obiektówfizycznych.
a) - materia to wszystkie obiekty o różnej od zera masiespoczynkowej
b) - materia to wszystkie obiekty złożone z elementarnychfermionów
c) - materia to wszystkie obiekty złożone z dwu (identyczne masy,czas życia, przeciwny znak ładunku el., addytywne wszystkie liczby
kwantowe) odmian cząstek elementarnych, która przeważa we
wszechświecie.
d) - materia to wszystkie obiekty wytwarzające grawitację i jejpodlegające czyli o niezerowej en.
3. Budowa atomu - at to podstawowy składnik materii.Złożony z elementarnych cząstek materii: i elektrony i
Nukleony = neutrony + protony. Masy w U: p-1; n-1; e-1/1840
. Ładunek: p 1; n 0; e -1. Atomy różnią ilością protonów w jądrze
(liczba atomowa = Z). Liczba protonów i neutronów to
liczba masowa = A.
Izotopy - ta sama liczba protonów a różna neutronów.
4. Liczby kwantowe - są 4 liczby: n- główna liczba kwantowa-kwantuje en. el. (1,2,…,7) lub (K ,L ,…,Q) - oznaczenie powłok;
l- poboczna liczba kwantowa- określa podpowłokę (s,p,d,f,g,h),
którą zajmuje el. I wyznacza kształt orbitali; m- magnetyczna liczb
a kwantowa- określa wzajemne położenie orbitali w przestrzeni i ilość
orbitali na danym poziomie, wartości: -1, 0, 1; spin s- kręt elektronu
wokół własnej osi, s=+- ½. (fermiony - cząstki o spinie połówkowym.
Najczęściej sptykane to protony, elektrony i neutrony)
5. Zakaz Pauliego. Rozmieszczenie elektronów w atomie - w atomienie mogą znajdować się dwa elektrony mające te same wart. Wszystkich
4 liczb kwantowych.| W stanie podstawowym atomu każdy elektron dąży
do zajęcia najniższego z możliwych poziomów energetycznych.
grupy - kolumny o podobnych własnościach, okresy - wiersze ukł.okresowego, nr okresu informuje ile powłok ma at., nr gr.= ilość elektronów na
ostatniej walencyjnej powłoce
6. Elementarny model atomu wodoru Bohra. Postulaty Bohra-model opracowany na podstawie wyników doświadczenia Rutherforda.
Z Eksperymentu wynikało że w at. musi być mała masywna bryła materii
(masa centralna która odbijała uderzające w jądro cząsteczki α). Na każdej
orbicie jest inny stal energetyczny el. Gdy jest na dozwolonej orbicie to nie
promieniuje en. Postulaty:
a)elektron nie może krążyć po dowolnej orbicie, ale tylko tych dla którychmoment pędu (kręt) el. jest wielokrotnością stałej Plancka h /2π. mevr=nh/2π
(n- główna liczba kwantowa, r- prom, v- prędk.)
b) Pomimo że el ma przyspieszenie to nie wypromieniowuje en., więc en jeststała.
Dozwolone poziomy energetyczne at wodoru. en-liczba kwantów(-13.59- n=1; -3.44 - n=2; -1.56 - n=3) c) promieniowanie elektromagnetyczne
zostaje wtedy wysyłane gdy elektron poruszający się po orbicie o całkowitej
en Ej zmienia swój ruch skokowo, tak że porusza się następnie po orbicie o en Ek.
Częstotliwość emitowanego lub pobieranego prom v =|Ej-Ek|/h (h*v - foton)
Kwant - porcja en., jaką at/ jądro może pobrać/oddać. Gdy emisja to at „idzie”
na niższy stan energetyczny i odwrotnie. Gdy są oddziaływania elektromagnetyczne
to kwant nazywa się fotonem.
7. Mechanika klasyczna a kwantowa- stała Plancka - W klasycznej h=0, wkwantowej h= 6,62*10-34 J*s
8. Rys historyczny powstania mechaniki kwantowej i jej podział na relatywistyczną i
nierelatywistyczną
Od 1900r. Planck, Einstein, Bohr i inni rozwijali teorie kwantowe próbując wyjaśnić wyniki
róznych eksperymentow poprzez wprowadzenie dyskretnych poziomow energetycznych.
W 1925 Heisenberg i Schrodinger sformułowali mechanike kwantowa, która wyjaśnił
poprzedzające ja teorie kwantowe.
W mechanice kwantowej wynik pomiaru fizycznego jest z natury rzadzony prawdopodobieństwe,
a teoria pokazuje jak obliczyc to prawdopodobieństwo. Mechanik kwantowa opisuje zachowanie
materii w malych odległościach.
9. Hipoteza de Broglie,a
De Broglie zapostulował odwrócenie zależności wyrażającej pęd fotonu stowarzyszonego z falą
elektromagnetyczną (zależności znanej z teorii fotonowej), czyli długość fali materii stowarzyszonej
z cząstką miała wyrażać się przez pęd cząstki.
![]()
λ - długość fali, h - stała Plancka (6,62*10-34 J*s), p - pęd cząstki
Każdej cząsteczce o energii E można również przyporządkować inną częstotliwość fali: f=E/h
10. Falowa natura materii
Fale materii, zwane też falami de Broglie'a jest to, alternatywny w stosunku
do klasycznego, (czyli korpuskularnego), sposób postrzegania obiektów
materialnych
. Według hipotezy dualizmu korpuskularno-falowego każdy obiekt może
być opisywany na dwa sposoby: jako cząstka/obiekt materialny albo jako
fala (materii). Pomysł opisu cząstek za pomocą fal pochodzi
od Louisa de Broglie'a, który w 1924 roku uogólnił teorię fotonową
. W tym czasie wiedziano już, że na potrzeby opisu niektórych
zjawisk fizycznych, z każdą falą elektromagnetyczną można
stworzyć pewną cząstkę -foton. Propozycja De Broglie'a
polegała na tym, aby każdej cząstce o różnym od zera pędzie
przypisać falę, o określonej długości i częstości.
Propozycja ta wychodziła naprzeciw wynikom eksperymentalnym,
które świadczyły, że w pewnych sytuacjach każda cząstka może
zachowywać się jak fala.
11. Prędkość falowa i grupowa fali
Prędkośc fazowa - prędkość pojedynczej fali.
Vf = E/ћk = h/2mS
Prędkość grupowa - prędkośc z jaka można przesłac sygnał lub energie w ośrodku.
Vg = dω/dk = ϛ/m
Dla falowodu:
a-szrokość fali
λ-długośc fali w próżni
Dla ośrodka niedyspersyjnego Vf=Vg=const. W prózni Vf=Vg=C
12. Doświadczalne potwierdzenie istnienia fal materii
????????????????
13. Prawo Bragga
Prawo Bragga sformułowano w 1913 roku przez W.L. Bragga. Jest to
równanie określające kierunek, w którym następuje tzw. Interferencyjne
odbicie promieni rentgenowskich od płaszczyzny sieciowej hkl
monokryształu (dyfrakcja fal).
W myśl równania Bragga odbicie promieni rentgenowskich o
długości fali λ zachodzi jedynie w takich kierunkach, określonych
przez kąt odbłysku Θ, dla których różnica dróg ΔS promieni odbitych
od dwóch sąsiednich równoległych płaszczyzn sieciowych jest równa
całkowitej wielokrotności długości fali.
![]()
n=1,2,3.. jest to tzw. rząd odbicia, czyli liczba długości fali, które mieszczą się w
różnicy dróg ΔS
d(hkl) - odległość między płaszczyznami
Równanie Bragga jest spełnione również podczas dyfrakcji cząstek.
14. Dualizm korpuskularno- falowy
Cecha wielu obiektów fizycznych (np: światła czy elektronów) polegająca na tym
, że w pewnych sytuacjach, zachowują się one jakby były cząstkami (korpuskułami),
a w innych sytuacjach jakby były falami.
Wg mechaniki kwantowej właściwie całą materie charakteryzuje ten dualizm. Każdej
cząstce, a nawet każdemu obiektowi makroskopowemu można przypisać
charakterystyczną dla niego funkcję falową, z drugiej strony każde oddziaływanie
falowe można opisać w katego
riach cząstek.
Jest on w sformalizowanym języku mechaniki kwantowej opisany równaniem
Schrodingera.
15. Transformacja Lorentza
Została utworzona w 1904 r. przez Henryka Antona Lorentza. Zauważył,
że nie tylko światło wyłamuje się z transformacji Galileusza. Również masa
nie jest wielkością stałą ani taką samą dla wszystkich obserwatorów, ale zależy
od układu odniesienia, z jakiego jest obserwowana i jest równa masie spoczynkowej
m0 kiedy ciało jest w spoczynku w układzie odniesienia, z którego jest ono obserwowane:
m=γ*m0 (γ=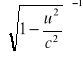
- nazywamy czynnikiem Lorentza)
Fundamentalna jej cechą jest oparcie się na szczególnej teorii względności Einsteina,
czyli że prędkość światła nie zależy od układu odniesienia.
Równania transformacji Lorentza: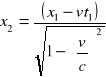
y2=y1
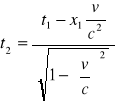
![]()
Niezmienniki transformacji Lorentza:
- prędkość światła jest nie zależna od układu odniesienia
- interwał - odległość zdarzeń w czasoprzestrzeni
- masa spoczynkowa
16. Lorentzowskie dodawanie prędkości
Definicja prędkości:
V = dr/dt
Składowe prędkości:
Vx = dx/dt; Vy; Vz
17. Prawo złożenia prędkości
Dla v/c ->0 transformacja prędkości Lorentza przechodzi w
transformacje prędkości Galileusza:
V2x=V1x - V; V2y=V1y; V2z=V1z
18. Masa i pęd w mechanice relatywistycznej
Masa chwilowa ciała o masie spoczynkowej mo
poruszającego się z prędkościa v jest równa:
Rozważając szczególny przypadek zderzeń można wykazać,
że pęd newtonowski (nierelatywistyczny) nie jest zachowany
przy zderzeniach cząstek mających prędkości v duże, tzn., że
v/c nie zmierza do zera.
![]()
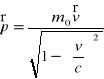
Równanie zachowania pędu izolowanego układu cząsteczek
![]()
19. Siła relatywistyczna
????????
20. Relatywistyczna energia kinetyczna
Energia kinetyczna (wzór relatywistyczny)
21. Relatywistyczna energia całkowita
Wiąże się z Ogólną Teorią Względności Alberta Einstein..
Zdefiniowana jest jako energia całkowita ciała izolowanego
od otoczenia, a więc nie znajdującego się pod wpływem ża
dnych potencjałów zewnętrznych. Einstein odkrył, że nawet
ciało znajdujące się w idealnym spoczynku ma pewien zasób
energii. Dla takiego nieruchomego ciała energia relatywistyczna
jest nazywana energią spoczynkową i definiuje ją słynny wzór
na równoważność masy i energii:
E = mc2
Energia (całkowita) ciała
Wyszukiwarka
Podobne podstrony:
Pytania i odpowiedzi FCS ost, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, S
Pstrona MO., POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 2, StudiaI
MiBM III, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 3, StudiaIII
Produkcja cegły czerwonej, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Seme
Bazy Danych wyklady sem III, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Se
TM2.x, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 2, StudiaII cz1,
CHEMIA FIZYCZNa v 2 1SCIAGA, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Se
Zagadnienia Matematyka2, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semest
powierzchniowa, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 3, Stud
Pstrona MD., POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 2, StudiaI
MiBM III, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 3, StudiaIII
mechana i mechana doświadczalna - tematy, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - M
Opracowane zagadnienia, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr
więcej podobnych podstron