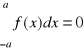
Pd

Zad.1

a) Pokazać, że jeżeli f jest ciągłą funkcją nieparzystą na przedziale
to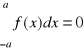
.

(zrobione na ćwiczeniach).

b) Uzasadnić, że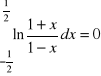
,
.

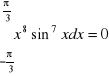
Zad.2 Obliczyć za pomocą całki oznaczonej pola figur ograniczonych liniami, wykonać rysunki

a)
,
,

b)
,
,
dla

d)
,
,

e)
,
,
,

f)
,
,
,

g)
,

h)
,
.

Zad.3 Wyznaczyć wartość średnią funkcji

a)
w przedziale

b)
w przedziale
.

Podać interpretację geometryczną.

zad.4 Wyznaczyć ekstrema funkcji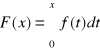
dla
jeżeli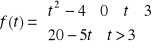

zad.5 Wyznaczyć funkcję
określoną wzorem

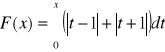
dla x≥0, b)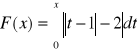
dla xႳ0.

Wykreślić funkcje podcałkowe i wyznaczone funkcje górnej granicy całkowania.

Podać interpretację geometryczną F(1), F(3) na obu wykresach. Co można powiedzieć o ciągłości i różniczkowalności funkcji podcałkowej i funkcji obliczonej. Podaj przedziały monotoniczności i ekstrema funkcji F, porównaj zachowanie F z zachowaniem funkcji podcałkowej.

Zad.6 Rozwiązać równanie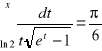
.

zad.7 Obliczyć całki niewłaściwe

a)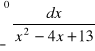
, b)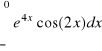
,

c)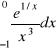
, d)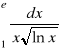
, e)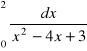

zad.8 Obliczyć pole figury ograniczonej krzywymi
,
,
,

odpowiedzi

zad.2 a)
; b)
, c)
; d)
; e)
; f)
, g)
h)

zad.3 a)
; b) 6.

Zad.5 a)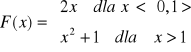
b)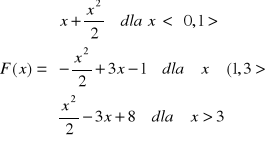

zad.6 x=2

Zad.7

a)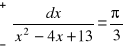

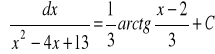
b)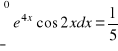

zad.2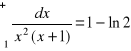

c)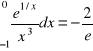
, d)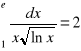
, e)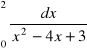
całka rozbieżna

zad.8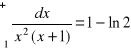

3