MATEMATYKA WYKŁAD NR 3

warunek

Własności:

1. Macierz odwrotna do macierzy odwrotnej jest macierzą bazową

2. Macierz transponowana i odwrotna równa się macierzy odwrotnej i transponowanej.

3. Odwrotny iloczyn macierzy A i B równa się iloczynowi odwrotnej macierzy A i odwrotnej macierzy B

OPERACJE ELEMENTARNE NA WIERSZACH MACIERZY

Wyróżniamy trzy typy działań elementarnych:

1. Zamiana miejscami dwóch wierszy macierzy

2. Mnożenie wybranego wiersza macierzy przez odwrotna liczbę
   

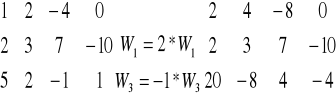
3. Dodanie do wybranego wiersza macierzy innego jej wiersza pomnożona przez dowolna liczbę
   

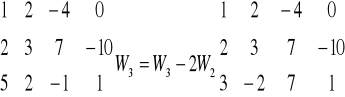
Definicja:

Macierz A i B o tych samych wymiarach nazywamy równoważnymi co zapisujemy A~B jeśli jedną z nich da się otrzymać z drugiej poprzez wykonanie skończonej liczby operacji elementarnych.

Celem wykonania operacji elementarnych na macierzy o „m” wierszy i „n” kolumnach jest przekształcenie wybranych kolumn tej samej macierzy w odpowiednie „m” elementarne wektory jednostkowe.

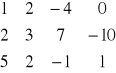
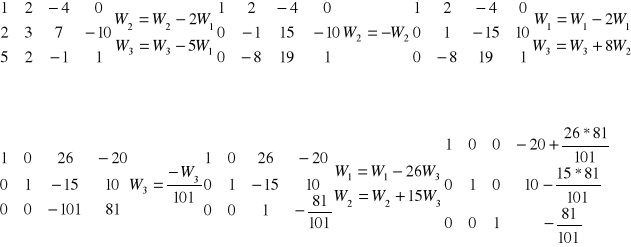
postać bazowa

Postacią bazową (kanoniczną) macierzy A nazywamy jej macierz równorzędną o maksymalnej liczbie kolumn będących różnymi wektorami jednostkowymi

Rząd macierzy - maksymalna liczba wektorów jednostkowych występujących jako kolumny w postaci bazowej macierzy

Wyznaczyć macierz bazową i rząd macierzy.

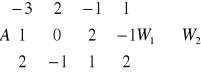
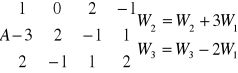
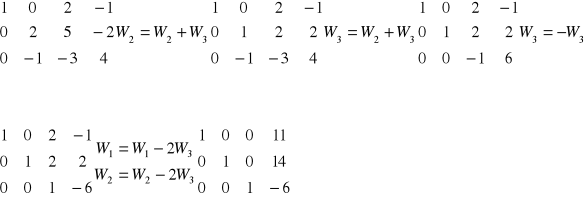
macierz bazowa

Rząd macierzy 3

Definicja:

Wyznacznikami stopnia „l” macierzy prostokątnej nazywamy wyznacznik macierzy kwadratowej stopnia „l” powstałych przez skreślenie w macierzy A odpowiedniej liczby wierszy i kolumn.

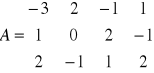
Wyznacz macierz bazową i rząd macierzy

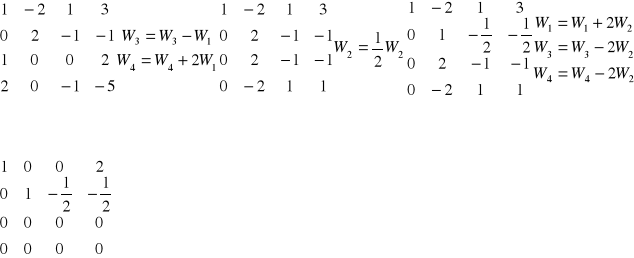
macierz bazowa

Rząd macierzy = 2

Rządem macierzy prostokątnej nazywamy najwyższy stopień różnych od 0 wyznaczników tej macierzy.

Twierdzenie:

Macierz kwadratowa stopnia „n” jest nieosobliwa wtedy i tylko wtedy gdy rząd A jest równy jej stopniowi

A~In

Wyznaczyć macierz odwrotną do macierzy

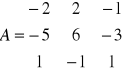
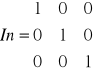
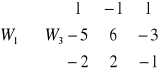
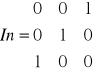
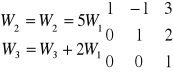
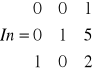
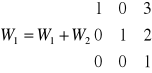
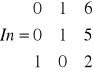
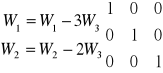
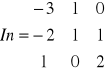
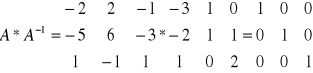
UKŁAD RÓWNAŃ LINIOWYCH:

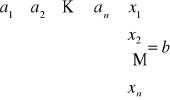
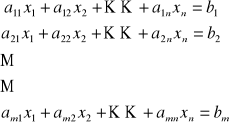
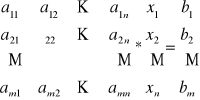
A - macierz współczynników

b - wektor wyrazów wolnych

x - wektor niewiadomych

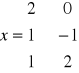
Rozwiązaniem szczególnym równania liniowego nazywamy każdy wektor którego współrzędne spełniają to równanie

Rozwiązaniem ogólnym równania liniowego nazywamy zbiór wszystkich rozwiązań szczególnych danego równania

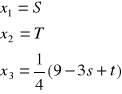
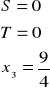
macierz rozszerzona układu równań

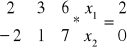
4