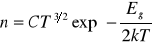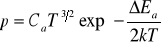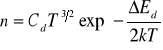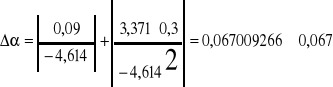Samul

Sprawozdanie 1

Temat: Pomiar zależności oporności metali i półprzewodników od temperatury.

1. WSTĘP

Ciała stałe ze względu na ich własności elektryczne można podzielić na przewodniki, półprzewodniki i dielektryki. Półprzewodniki to ciała, których przewodność właściwa jest mniejsza od przewodności dobrych przewodników, ale znacznie większa od przewodności dielektryków, mieści się ona w granicach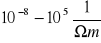
.

Takie kryterium podziału jest jednak bardzo przybliżone, o wiele ważniejszym czynnikiem jest struktura elektronowa ciała, z której wynikają wszystkie jego własności (elektryczne, optyczne itd.). W przewodnictwie prądu w ciałach stałych uczestniczą elektrony, które mają największą energię - znajdujące się na zewnętrznych (walencyjnych) powłokach atomu. Ponieważ w ciele stałym odległości między atomami w sieci krystalicznej są bardzo niewielkie, na skutek oddziaływań sąsiednich atomów elektrony walencyjne przestają być związane ze `swoim' atomem, a stają się uwspólnione. W przewodnikach (metalach) pasmo przewodnictwa `zachodzi' na pasmo walencyjne, dlatego wystarczy niewielka temperatura lub pole elektryczne, aby elektrony walencyjne przeszły na wyższe poziomy energii i stały się uwspólnione (a co za tym idzie - aby popłynął prąd). Natomiast w półprzewodnikach i w dielektrykach pomiędzy pasmem walencyjnym a pasmem przewodnictwa znajduje się pasmo energii zabronionej - elektrony nie mogą zajmować tego pasma. Pasmo to zwane jest też przerwą energetyczną. Wielkość przerwy energetycznej odróżnia dielektryki (duża przerwa wzbroniona) od półprzewodników (przerwa wielokrotnie mniejsza). Dlatego też prawdopodobieństwo przejścia elektronu walencyjnego do pasma przewodnictwa jest wielokrotnie mniejsze w dielektrykach niż w półprzewodnikach.

Przewodność ciała ogólnie zależna jest od ilości swobodnych nośników i od ich ruchliwości.

W półprzewodnikach przewodność wyraża się wzorem:

,

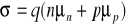
gdzie q - ładunek elektronu, n,p - koncentracja nośników,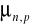
- ruchliwość nośników.

Dla półprzewodnika szerokość przerwy energetycznej mieści się w granicach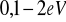
. Mała szerokość przerwy sprawia, że energia drgań cieplnych atomów sieci krystalicznej, proporcjonalna do temperatury ciała, może już w relatywnie niskich temperaturach być wystarczająca do przeniesienia części elektronów walencyjnych do pasma przewodnictwa. Koncentracja elektronów swobodnych n wyraża się następującą zależnością:

,

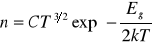
gdzie k - stała Boltzmana, C - stała zależna od rodzaju półprzewodnika, E_g - szerokość przerwy wzbronionej, T - temperatura wyrażona w Kelvinach. Widać tu, że ilość swobodnych elektronów jest bardzo silnie (wykładniczo) zależna od temperatury (jest to cecha specyficzna półprzewodników, ponieważ w metalach ilość swobodnych elektronów jest praktycznie niezależna od temperatury). Bardzo łatwo zmienić ilość swobodnych elektronów w półprzewodniku w procesie domieszkowania. Do kryształu czystego półprzewodnika wprowadza się celowo atomy obcych pierwiastków, które wprowadzają do modelu pasmowego półprzewodnika dodatkowe poziomy energetyczne umieszczone tuż nad granicą pasma walencyjnego (domieszki akceptorowe, półprzewodnik typu P) lub tuż pod granicą pasma przewodnictwa (domieszki donorowe, półprzewodnik typu N). Powoduje to wielokrotne zwiększenie koncentracji ładunków dodatnich - dziur - w przypadku domieszek akceptorowych, lub ładunków ujemnych - elektronów - w przypadku domieszek donorowych. Koncentracja nośników większościowych - dziur - w półprzewodniku typu P opisana jest wzorem:

,

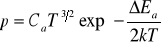
elektronów w półprzewodniku typu N:

.

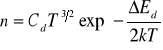
Ruchliwość nośników w półprzewodniku jest zależna od temperatury według następującego wzoru:

,

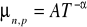
gdzie A i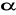
to stałe zależne od materiału półprzewodnika oraz od dominującego mechanizmu rozpraszania (na drganiach cieplnych sieci krystalicznej - fononach lub na zjonizowanych atomach domieszek).

Uwzględniając powyższe zależności przewodności w półprzewodniku od temperatury otrzymamy następujący wykres:

Rys. 1. Wykres zależności przewodności od 1/T - odcinek a-b - jonizacja domieszki, b-c - obszar nasycenia i pełnego zjonizowania domieszki, c-d - generacja par elektron-dziura pod wpływem temperatury.

Dla metali przewodność można wyrazić następującym wzorem:

W metalach koncentracja nośników prądu jest niezależna od temperatury i jest w przybliżeniu równa koncentracji atomów. Dlatego też główny wpływ na przewodność ma zmiana ruchliwości nośników.

Na ruchliwość ma wpływ głównie zmiana szybkości rozpraszania nośników wraz ze zmianą temperatury. W metalach daje się wyróżnić dwa typy rozpraszania nośników. Pierwszy to rozpraszanie na fononach, które staje się coraz szybsze wraz ze wzrostem temperatury (drgania się nasilają i zwiększa się prawdopodobieństwo zderzenia). Zależność ta w wysokich temperaturach jest w przybliżeniu liniowa i oporność metalu można wyrazić wzorem:

,

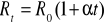
gdzie R₀ - oporność w temperaturze 0°C, R_t - oporność w temperaturze t°C, natomiast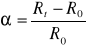
to temperaturowy współczynnik oporności w zakresie od 0 do t°C.

Drugi typ rozpraszania to rozpraszanie na defektach sieciowych. Rozpraszanie to jest niezależne od temperatury i dominuje w bardzo niskich temperaturach. Rozpraszanie to powoduje oporność R_i zwaną często opornością resztkową. Obydwie oporności R_t i R_i są addytywne zgodnie z regułą Matthiessena:

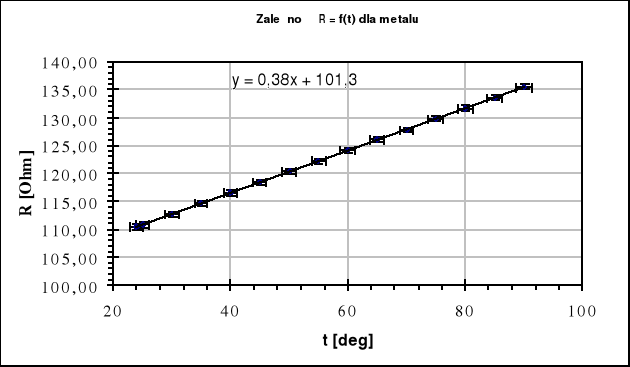
Wykres uwzględniający obydwa mechanizmy rozpraszania - obrazujący zależność oporności metalu od temperatury wygląda następująco:

Rys.2 Zależność oporności R od temperatury dla metali. 1 - przewodnik, 2 - nadprzewodnik.

1.Układ pomiarowy:

Przyrządy użyte w ćwiczeniu:

• Komora pomiarowa zawierająca badany metal (Pt) i stop półprzewodnikowy NTC-210;

• Multimetr typu 1331, (±.0.2 % wartości mierzonej+0.1% podzakresu);

• Multimetr typu 1321, (±.0.2 % wartości mierzonej+0.1% podzakresu);

• Autotransformator typu AR 201;

• Transformator ochronny;

• Termometr YF-160A ±( 0,3%+1°C)

2.Wyniki pomiarów

Pomiary dla metalu (Pt)

T[°C] °C	Δt[°C]	Rm [Ω]	ΔRm[Ω]
24	1,07	110,4	0,420
25	1,07	110,8	0,421
30	1,09	112,7	0,425
35	1,10	114,6	0,429
40	1,12	116,5	0,433
45	1,13	118,4	0,436
50	1,15	120,3	0,440
55	1,16	122,2	0,444
60	1,18	124,1	0,448
65	1,19	126,1	0,452
70	1,21	127,8	0,455
75	1,22	129,8	0,459
80	1,24	131,7	0,463
85	1,25	133,6	0,467
90	1,27	135,5	0,471

Δt=(t*0,003)+1°C

z programu „Regresja” wyliczyłem iż

A=0,38 ±0,0004824

B=101,3 ±0,02855

Y=0,38x+101,3

α=0,003751233

σa= 0,0123~0,02

σb= 0,404~0,5

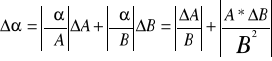
=0,00021664

pomiary dla półprzewodnika NTC-210

t [°C]	T[K]	ΔT[K]	1000/T[K^-1]	R[Ω]	ΔRs [Ω]	lnRs
24	297	1,90	3,37	834	1,87	6,726
25	298	1,90	3,36	816	1,83	6,704
30	303	1,91	3,31	678	1,56	6,519
35	308	1,93	3,25	571	1,34	6,347
40	313	1,94	3,20	475	1,15	6,163
45	318	1,96	3,15	420	1,04	6,040
50	323	1,97	3,10	356	0,91	5,874
55	328	1,99	3,05	300	0,8	5,703
60	333	2,00	3,01	253	0,71	5,533
65	338	2,02	2,96	212	0,62	5,356
70	343	2,03	2,92	189	0,58	5,241
75	348	2,05	2,88	166	0,53	5,112
80	353	2,06	2,84	143	0,49	4,963
85	358	2,08	2,80	122	0,44	4,804
90	363	2,09	2,76	105	0,41	4,654

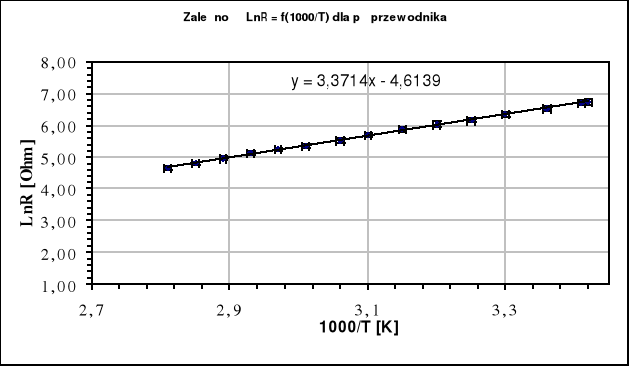
z programu „Regresja” wyliczyłem iż

A=3,371 ±0,03123

B=-4,614 ±0,09589

σa= 0,0827~0,09

σb= 0,271~0,3

k=1,3806 10-23 J/K - stała Boltzmanna

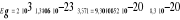
[ J ]

Jak wiadomo 1J
6,2415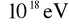
, można więc obliczyć wartość szerokości przerwy w elektronowoltach:

Eg=0,52 ±0,015[eV]

Wnioski:

W pierwszej próbce znajdował się metal a w drugiej półprzewodnik. Kiedy temperatura rosła rezystancja metalu rosła natomiast półprzewodnika malała. Energia potrzebna do przebicia się przez warstwę zaporową w półprzewodniku mieści się w normie między 0,1 do 2eV. Otrzymane wyniki potwierdziły założenia teoretyczne. Zależność ta dla metali jest liniowa a dla półprzewodników zależność lnR jest również liniowa, co potwierdzają aproksymacje. Nieliniowość w niektórych punktach wynikała prawdopodobnie ze złego odczytu i nieustabilizowanej temperatur

---