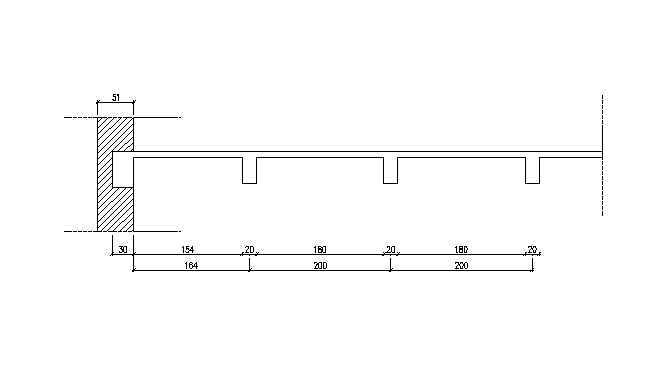
SCHEMAT STATYCZNY
II. Obliczenia płyty żelbetowej
Obliczenia statyczne

SCHEMAT STATYCZNY
Zestawienie obciążeń.
L.p. |
Wyszczególnienie i obliczenie wartości |
Obc. charakt. |
Wsp. obc. |
Obciążenie obliczeniowe |
|||
|
|
|
|
|
|
||
1 |
Posadzka: lasriko bezspoinowe gr.20mm |
0,44 kPa |
1,3 (0,8) |
0,57 kPa |
0,35 kPa |
||
2 |
Płyta żelbetowa gr. 8 cm 0,08 x 24,0 |
1,92 kPa |
1,1 (0,9) |
2,11 kPa |
1,73 kPa |
||
3 |
Tynk cem.-wap., gr.1,5 cm 0,015 x 19,0 |
0,29 kPa |
1,3 (0,8) |
0,38 kPa |
0,23 kPa |
||
Obciążenie stałe |
|||||||
Obciążenie zmienne |
1,2 |
|
|||||
Obciążenie całkowite |
|
|
|||||
![]()
![]()
Obliczenie momentów zginających
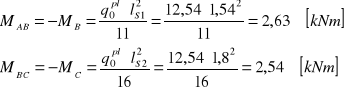
1.3.Obliczeniewspółczynników w zależności od stosunku pomax/qomax =9,48/3,06=3,10
α=0,291;
β1=-0,0215;
β2=-0,0083.
1.4.Zasięg momentu podporowego w skrajnym przęsle
a1 = α ⋅ lo =0,291⋅1,54 = 0,45 m
1.5.Ujemny moment w przęśle B - C
M1 = β1⋅ l22 ⋅(g+p) =-0,0215 ⋅ 1,802 ⋅ 12,54 = -0,87 kNm
1.6.Ujemny moment w przęśle C - D
M2 = β1⋅ l22 ⋅(g+p) = -0,0083 ⋅ 1,802 ⋅ 12,54 =-0,337 kNm
1.7.Ujemny moment w przęsłach
M = 1/3 ⋅ Mc + M1 = -1/3 ⋅ 2,54 -0,87= -1,72 kNm
2.Wymiarowanie płyty
przyjęto beton B25 - fcd =13,3 MPa =13300 kPa
stal AI - fyd=210 MPa = 210000 kPa
d = h - a - ∅/2 = 8 - 2- 0,5=5,5 cm α= 1
Przęsło A - B i podpora B
![]()
odczytano dla 0,067 ζ= 0,965 (tabela 2-6)
potrzebny przekrój zbrojenia :
![]()
przyjęto pręty ∅6 co 10 cm o Fa=2,83 cm2 > 2,359 cm2. (tablica IV)
Przęsło B - C i podpora C
![]()
odczytano dla 0,067 ζ= 0,965 (tabela 2-6)
potrzebny przekrój zbrojenia :
![]()
przyjęto pręty ∅6 co 10 cm o Fa=2,2,83 cm2 > 2,278 cm2. (tablica IV)
2.3.Zbrojenie na zastępczy moment :
w przęśle B-C
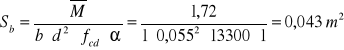
odczytano dla 0,048 ζ= 0,975 (tabela 2-6)
potrzebny przekrój zbrojenia :
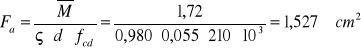
przyjęto pręty ∅ 8 co 30 cm o Fa=1,68 cm2 >1,527 cm2. (tablica IV)
w przęśle C-D
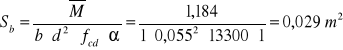
odczytano dla 0,039 ζ= 0,980 (tabela 2-6)
potrzebny przekrój zbrojenia :
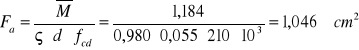
przyjęto pręty ∅ 8 co 30 cm o Fa=1,68 cm2 >1,046 cm2. (tablica IV)
Zbrojenie rozdzielcze
przyjęto pręty ∅ 4,5 co 25 cm o Fa=0,64 cm2 > 1/10 ⋅ Fa = 1/10⋅ 2,3 =0,236 cm2. (tablica IV)
lS2
lS2
lS1
![]()
lS2
lS1