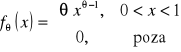
PROJEKTOWANIE BADAŃ i METODY ANALIZY STATYSTYCZNEJ I

Wybrane zagadnienia weryfikacji hipotez statystycznych

Zad. 1

Zmienna losowa X ma rozkład o gęstości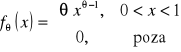
,
.

Badamy hipotezę
wobec hipotezy alternatywnej
. Obszar odrzucenia hipotezy
jest wyznaczony nierównością
,
i jest ustalone. Obliczyć prawdopodobieństwo błędu I i II rodzaju oraz wyznaczyć moc tego testu.

Zad. 2

Z populacji, w której cecha X ma rozkład normalny
wylosowano n-elementową próbę prostą. Wysunięto hipotezę
wobec hipotezy alternatywnej
.
Do zweryfikowania tej hipotezy proponuje się test o obszarze krytycznym postaci
. Wyznaczyć t, tak aby otrzymać test o prawdopodobieństwie błędu I rodzaju 0,05. Jak liczna powinna być próba losowa, aby prawdopodobieństwo błędu II rodzaju nie było większe niż 0,05.

Zad. 3

Niech
będzie prostą próbą losową pobraną z rozkładu normalnego
. Testujemy hipotezę
wobec hipotezy alternatywnej
, przy czym obszar krytyczny testu jest postaci
. Wyznaczyć stałą
tak, aby poziom istotności
. Wyznaczyć funkcję mocy tego testu w zależności od m. Czy test ten jest nieobciążony? Czy test ten jest zgodny?

Zad. 4

Niech
będzie prostą próbą losową pobraną z rozkładu normalnego
. Przypuśćmy, że weryfikujemy hipotezę
za pomocą testu z obszarem odrzucenia
.

Jaka jest moc tego testu przy
i
?

Zad. 5

Niech X będzie zmienną losową z rozkładu Erlanga o gęstości

.

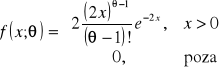
1. Testujemy hipotezę
   wobec hipotezy alternatywnej
   . Dysponując pojedynczą obserwacją, znaleźć test najmocniejszy przy
   .

2. Wyznaczyć moc tego testu.

Zad. 6

Podać końcową postać statystyki
używanej do testu ilorazu wiarygodności służącego do testowania hipotezy
wobec hipotezy alternatywnej
, jeżeli n-elementowa próba prosta pochodzi z rozkładu wykładniczego o funkcji gęstości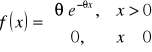
.

Zad. 7

Zmienna losowa X ma rozkład Pascala o funkcji prawdopodobieństwa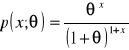

dla
,
. Z rozkładu tego została wylosowana dwustuelementowa próba prosta, w której zaobserwowano
. Przyjmując poziom istotności
należy zweryfikować hipotezę
wobec hipotezy alternatywnej
.

Zad. 8

Niech
będzie prostą próbą losową pobraną z rozkładu Poissona o funkcji prawdopodobieństwa
,
. Rozważmy zagadnienie weryfikacji hipotezy
przeciwko
. Znaleźć obszar krytyczny testu ilorazu wiarogodności na poziomie istotności
, jeśli n jest duże.

Zad. 9

Niech
będzie prostą próbą losową pobraną z rozkładu geometrycznego o funkcji prawdopodobieństwa
,
. Rozważmy zagadnienie weryfikacji hipotezy
wobec hipotezy
. Znaleźć obszar krytyczny testu ilorazu wiarogodności na poziomie istotności
, jeśli n jest duże.

1

---