WEWNĄTRZSZKOLNY KONKURS MATEMATYCZNY

LIGA ZADANIOWA

etap 4 - odpowiedzi

Klasy I

4. Rozwiąż układ równań:

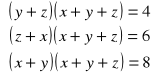
Odp.

Dodam do siebie równania stronami:

Wyłączę wspólny czynnik przed nawias:

. Po podzieleniu obustronnie przez 2 otrzymuję:
.

Stąd:
lub

Gdy

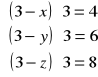
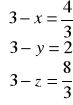
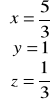
Gdy

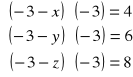
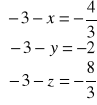
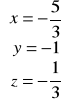
Odp.
lub
.

Klasy II

4. Piszemy w kolejności rosnącej kwadraty liczb całkowitych dwucyfrowych:
,
,
, …, a następnie obliczamy te kwadraty i do każdego z otrzymanych wyników stosujemy operację dodawania cyfr tyle razy, aż otrzymamy liczbę jednocyfrową (np.
). Jaka jest trzynasta liczba dwucyfrowa, której kwadrat, po zastosowaniu operacji dodawania cyfr, daje wynik końcowy równy 7?

Odp. Liczba
i suma cyfr liczby
w wyniku dzielenia przez 9 daje taką samą resztę. Szukamy liczb, których suma cyfr kwadratu sumy ich cyfr (ewentualnie sumy cyfr sumy ich cyfr) wynosi 7. Jedynie
i
. Stąd suma cyfr szukanych liczb musi być równa 4, 5, 13 lub 14. Oto kolejne liczby dwucyfrowe, które w wyniku powyższych operacji dadzą wynik 7: 13, 14, 22, 23, 31 32, 40, 41, 49, 50, 58, 59, 67, 68, ….

Trzynastą liczbą w tym ciągu jest 67.

Odp. 7

Klasy III

4. Wykaż, że prawdziwa jest nierówność
.

Odpowiedź:

Zwróćmy uwagę, że obydwie strony tej nierówności są dodatnie. Funkcja
jest rosnąca dla argumentów dodatnich. Stąd możemy uzyskać nierówność równoważną podnosząc nierówność obustronnie do kwadratu:

Iloczyn pierwiastków jest równy pierwiastkowi z iloczynu, stąd:

. Po podzieleniu obustronnie przez 2:

Obydwie strony tej nierówności są dodatnie, stąd mogę obie strony nierówności podnieść do kwadratu:

.

Co należało udowodnić.

Uwaga. Przy podnoszeniu obydwu stron nierówności do kwadratu, trzeba wpierw sprawdzić jakiego są znaku. Świadczyć może o tym przykładowa nierówność:
. Zwróćcie uwagę, że
.