W celu obliczenia wartości współczynnika załamania n obliczamy wartość kąta ϕ z wzoru: 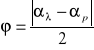
(5)
Nr ćwiczenia 301 |
Data wykonania ćwiczenia 20.10.2004 |
Kierunek studiów Mechanika i Budowa Maszyn |
Grupa M4 |
Wykonała Agnieszka Pachała |
Data oddania sprawozdania 03.11.2004 |
Semestr III |
Ocena |
Prowadzący Dr Izabela Hanyż |
Temat ćwiczenia Wyznaczanie współczynnika załamania światła metodą najmniejszego odchylenia w pryzmacie |
||
WSTĘP
Promień światła padając na granicę pomiędzy dwoma ośrodkami tzn. przy przejściu z jednego ośrodka do drugiego ulega załamaniu (rys.1). Kąt padania α, to kąt zawarty między prostopadłą do obydwu ośrodków a promieniem padającym. Kąt załamania, to kąt zawarty między tą samą prostopadłą a promieniem załamanym. Załamanie światła na powierzchni rozgraniczającej dwa ośrodki opisane jest prawem Snella.
(1)
Rys.1. Załamanie światła w pryzmacie
Do praktycznego wyznaczania współczynnika załamania światła stosuje się jednak wzór w innej postaci ze względu na niedogodność i niedokładność wyznaczania kątów padania i załamania.
W naszym ćwiczeniu wykorzystujemy tylko dwie płaszczyzny pryzmatu, tworzące między sobą kąt ϕ, zwany kątem łamiącym. Promień świetlny padający na pryzmat ulega dwukrotnemu załamaniu i zostaje odchylony o pewien kąt ϕ, zależny od kąta padania α oraz kąta od kąta łamiącego ϕ. Na podstawie rys. Możemy wyrazić kąt odchylenia następująco:
(2)
Kąt padania możemy tak dobrać, by promień biegnący wewnątrz pryzmatu był prostopadły do dwusiecznej kąta łamiącego ϕ. W tej sytuacji bieg promienia jest symetryczny, tzn. α1=α2 oraz β1=β2, a kąt odchylenia - najmniejszy z możliwych dla danego pryzmatu. Biorąc pod uwagę, że 2β=ϕ, otrzymujemy:
(3)
Podstawiając wyrażone powyżej wartości α i β do wzoru definiującego współczynnik załamania, otrzymamy:
(4)
Stosując powyższy wzór możemy wyznaczyć n na podstawie pomiarów kąta łamiącego i kąta najmniejszego odchylenia.
POMIARY
W celu obliczenia wartości współczynnika załamania n obliczamy wartość kąta ϕ z wzoru: 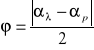
(5)
Dla pryzmatu z ćwiczenia laboratoryjnego otrzymaliśmy pomiary:
![]()
![]()
![]()
stąd mamy:![]()
, za dokładność pomiaru przyjmujemy ![]()
Aby obliczyć współczynnik załamania z następującego wzoru:
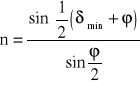
(6)
potrzebujemy jeszcze kąt najmniejszego odchylenia, który obliczymy z wzoru:
![]()
(7)
Dla poszczególnych filtrów mamy:
Numer filtra (kolor) |
Długość fali |
|
|
|
3 (czerwony) |
675 |
135°11' |
105°57' |
14°44' |
4(czerwony) |
656 |
135°12' |
105°56' |
14°46' |
5(pomarańczowy) |
600 |
135°15' |
105°54' |
14°51' |
6(pomarańczowy) |
589 |
135°17' |
105°52' |
14°55' |
7(zielony) |
554 |
135°20' |
105°50' |
15° |
8(niebieski) |
500 |
135°26' |
105°46' |
15°10' |
9(fioletowy) |
439 |
135°35' |
105°37' |
15°28' |
W tym przypadku również za dokładność pomiaru przyjmujemy ![]()
Wartość kąta dla promienia, który nie przeszedł przez pryzmat wynosi 120°36'
Wstawiając do wzoru (4) otrzymujemy wyniki:
Długość fali |
Współczynnik załamania n |
dn |
675 |
1,506 |
0,077 |
656 |
1,507 |
0,077 |
600 |
1,509 |
0,077 |
589 |
1,513 |
0,077 |
554 |
1,515 |
0,077 |
500 |
1,521 |
0,077 |
439 |
1,535 |
0,077 |
Błąd pomiaru współczynnika załamania n obliczamy za pomocą różniczki zupełnej:
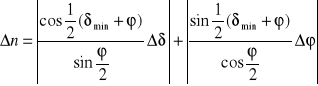
błędy dδ i dϕ są dokładnością spektrometru i wynoszą: δ = 0.02° i dϕ = 0.02°
Na podstawie powyższych danych wykreślić możemy krzywą dyspersji dla poszczególnych długości fal:
Błąd pomiaru wynosi ![]()
0,077
WNIOSKI