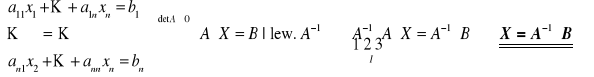
UKŁADY RÓWNAŃ LINIOWYCH

I UKLADY CRAMERA

1) Rozwiązywanie metodą macierzową układu równań Cramera (n równań z n niewiadomymi i nieosobliwą macierzą współczynników A):

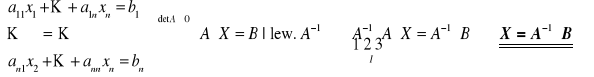
2) Rozwiązywanie za pomocą gotowych wzorów Cramera :

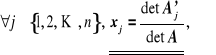
gdzie

- wyznacznik macierzy powstałej z macierzy A przez zastąpienie i-tej kolumny kolumną wyrazów wolnych B.

Szkic dowodu:

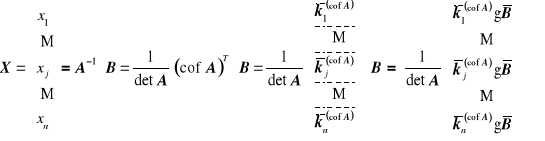
stąd

, gdzie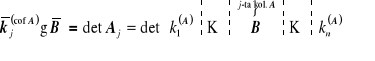
.

II UKLADY OGÓLNE (twierdzenie Kroneckera-Capelliego)

Podamy teraz warunki rozwiązalności ogólnego układu równań liniowych, zapisanego w symbolice macierzowej, tzn.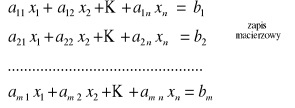

,

gdzie
jest zadaną macierzą współczynników układu,
- zadanym wektorem kolumnowym wyrazów wolnych,
- wektorem kolumnowym niewiadomych.

Zdefiniujmy w tym celu macierz utworzoną z macierzy A przez dołączenie do niej dodatkowej
kolumny wyrazów wolnych B . Będziemy ją oznaczać przez U i nazywać macierzą uzupełnioną (rozszerzoną), czyli

.

Twierdzenie (Kroneckera-Capelliego). Mogą zajść dwa przypadki:

1. układ rozwiązalny:
   ,

2. układ sprzeczny:
   

(ściślej:
)

W przypadku 1):

układ posiada dokładnie jedno rozwiązanie
,

układ posiada nieskończenie wiele rozwiązań zależnych od
parametrów

Podamy algorytm uzyskania rozwiązań w przypadku 1):

1. Niech M jest podmacierzą kwadratową stopnia r macierzy współczynników A o wyznaczniku różnym od 0, zwaną macierzą bazową (istnieje, bo
   ). Zmienne, których współczynniki występują w tej macierzy nazywamy zmiennymi bazowymi (jest ich r).

2. Usuwamy z układu te równania, których współczynniki nie wchodzą w skład macierzy M, otrzymując układ równań równoważny wyjściowemu.

3. Przyjmujemy jako dowolne parametry rzeczywiste te zmienne niebazowe (jest ich
   ), których współczynniki nie występują w macierzy bazowej M i składniki z tymi parametrami przenosimy do kolumny wyrazów wolnych.

4. Rozwiązujemy otrzymany w ten sposób układ Cramera stopnia r ze zmiennymi bazowymi i macierzą współczynników M oraz z kolumną wyrazów wolnych zawierających parametry.

METODA ELIMINACJI GAUSSA I JORDANA -GAUSSA

Idea:

Rozwiązywanie układów równań liniowych w oparciu o twierdzenie Kroneckera-Capelliego dla dużej liczby równań i niewiadomych staje się na ogół kłopotliwe. Dlatego w obliczeniach numerycznych stosuje się metodę opartą na sukcesywnej eliminacji (rugowaniu) niewiadomych zwaną metodą elimimacji Gaussa lub metodą Jordana -Gaussa.

Idea tej metody polega na przekształcaniu równoważnym wyjściowego dowolnego układu
za pomocą operacji na równaniach (inaczej operacji na wierszach macierzy
nie zmieniających jej rzędu) do postaci

(w metodzie Gaussa)

gdzie

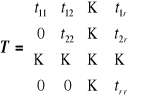
jest tzw. macierzą trójkątną (z zerami pod główną przekątną) oraz

(w metodzie Jordana-Gaussa)

z macierzą jednostkową
.

Przykład: (skrócony zapis układu: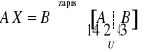
)

Tw. K-C:
, układ ma dokładnie jedno rozwiązanie

Przykłady:

1) Rozwiązać układy równań (lub stwierdzić, że układ jest sprzeczny):

a)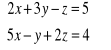
b)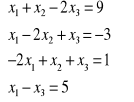
.

2) Dany jest układ równań z parametrem
:

.

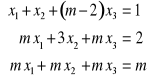
Zbadać istnienie rozwiązań i podać rozwiązania, gdy istnieją, w zależności od

parametru m .

3