108Doman, Polibuda, studia, S12, Fiza, Lab, Fizyka- laboratoria, Laborki- inne2

nr ćwiczenia 108

data 30.11.

2006r.

Maciej Domański

Wydział

BiIŚ

semestr I

Grupa B2

nr lab. 3

Prowadzący

dr Andrzej Krzykowski

przygotowanie

wykonanie

ocena ostatecz.

Wyznaczanie modułu Younga metodą ugięcia.

W czasie działania siły na podłużny pręt w kierunku prostopadłym do jego długości, doznaje on ugięcia. Ugięcie to oznaczamy przy pomocy tzw. strzałki ugięcia S, która jest proporcjonalna do działającej siły F, jak również zależy ona do wymiarów geometrycznych pręta, sposobu mocowania i materiału z którego go wykonano.

Gdy na umocowany jednostronnie pręt działa siła to górne jego warstwy ulegają wydłużeniu, natomiast dolne - skróceniu (są ściskane).Jeżeli nie działają żadne siły przekroje prostopadłe pręta są równoległe, natomiast po przyłożeniu siły tworzą pewien kąt ϕ. Jeżeli weźmiemy pod uwagę element pręta o długości Δx, grubości Δy i szerokości b, znajdujący się w odległości x od krawędzi mocowania pręta i na wysokości y powyżej jego warstwy środkowej, to zauważymy, że na skutek ugięcia pręta badana warstwa uległa wydłużeniu o Δϕ. Zgodnie z prawem Hooke'a wydłużenie jest proporcjonalne do siły i długości początkowej oraz odwrotnie proporcjonalne do pola przekroju.

(1)

,gdzie:

działająca siła

moduł Younga

Taka sama siła jak , lecz o przeciwnym zwrocie działa na warstwę elementarną położoną symetrycznie poniżej warstwy neutralnej N .Moment siły względem warstwy N wynosi:

(2)

Całkowity moment siły działający na wszystkie warstwy obliczymy całkując równanie (1) względem y po całej grubości pręta

(3)

Oznaczmy

(4)

to otrzymamy:

(5)

Powyższe wyrażenie otrzymaliśmy rozpatrując odkształcenie pręta. Bezpośrednia przyczyna tego ugięcia jest siła F. Moment tej siły wynosi względem przekroju 2 F(l-(x+Δx)) w ogólności przy zaniechaniu Δx :

Μ = ( l - x )F (6)

Kąt ϕ jest również zawarty pomiędzy stycznymi do pręta w punktach, gdzie przekroje 1 i 2 przecinają górną powierzchnię. Możemy więc napisać

(7)

Gdy uwzględnimy powyższy wniosek w równaniu (5) oraz porównamy równania (5) i (6) otrzymamy elementarną strzałkę ugięcia

A całkowita strzałkę ugięcia otrzymamy całkując to wyrażenia dla wszystkich Δx

(8)

Jeżeli teraz, że przekrój naszego pręta jest prostokątem o wysokości h i szerokości b to H po scałkowaniu równania (4) daje:

natomiast, gdy przekrój pręta jest kołem otrzymujemy:

Podstawiając odpowiednio H do otrzymanego wzoru (8), otrzymamy równania na strzałkę całkowitą dla pręta jednostronnie umocowanego (o przekroju prostokąta i koła):

Po odpowiednim przekształceniu powyższych równań otrzymamy odpowiadające im wzory na strzałkę całkowitą dla pręta podpartego dwustronnie i obciążonego na środku. Następnie przekształcimy je do postaci nam potrzebnej. W ostateczności otrzymamy następujące wzory na dzięki którym będziemy mogli wyznaczyć moduł Younga:

Przebieg doświadczenia:

Zmierzyć wymiary poprzeczne pręta.
Zmierzyć odległości między krawędziami podpierającymi i wyznaczyć środek pręta.
Wypoziomować katetometr i przy jego pomocy wyznaczyć położenie górnej krawędzi pręta nieobciążonego
.
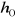
Obciążając kolejno środek pręta ciężarkami (o znanej masie), odczytywać położenia górnej krawędzi h_n pręta obciążonego.
Powtórzyć pomiary strzałki ugięcia podczas zmniejszania obciążenia.
Sporządzić wykres zależności strzałki ugięcia od siły obciążającej.
Obliczyć metodą regresji liniowej współczynnik nachylenia i jego błąd.
Obliczyć moduł Younga, wykorzystując równanie
.
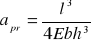
Obliczyć błąd modułu Younga.
Podać ostateczną wartość wyniku i błędu.

Pomiary i obliczenia:

h₀ - pierwotne położenie pręta

h_n- kolejne położenie pręta

b - szerokość pręta

h - grubość pręta

l - odległość między podporami

h,b = 8mm = 0,008m

l = 648mm = 0,648m

h₀ = 607,73 [mm]

Δb, Δh, Δl = 1 [mm]

obliczanie modułu Younga

obliczanie współczynnika nachylenia

Lp.	m [kg]	h_n [mm]	S [mm]		E	ε_i	a	ε_i
1	0	607,73	0
2	0,2	607,3	0,43		7,570*10¹⁰	0,443*10¹⁰	2,194*10^-4	13,797*10^-6
3	0,4	606,83	0,9		7,234*10¹⁰	0,107*10¹⁰	2,296*10^-4	3,593*10^-6
4	0,5	606,55	1,18		6,896*10¹⁰	0,230*10¹⁰	2,408*10^-4	7,631*10^-6
5	0,7	606,14	1,59		7,165*10¹⁰	0,039*10¹⁰	2,318*10^-4	1,407*10^-6
6	1,0	605,51		2,22	7,331*10¹⁰	0,205*10¹⁰	2,265*10^-4	6,654*10^-6
7	1,2	604,88		2,85	6,853*10¹⁰	0,274*10¹⁰	2,423*10^-4	9,162*10^-6
8	1,4	604,49		3,24	7,033*10¹⁰	0,094*10¹⁰	2,362*10^-4	2,967*10^-6
9	1,5	604,27		3,46	7,056*10¹⁰	0,071*10¹⁰	2,354*10^-4	2,189*10^-6
10	1,7	603,81		3,92	7,058*10¹⁰	0,068*10¹⁰	2,353*10^-4	2,109*10^-6
11	1,9	603,39		4,34	7,125*10¹⁰	0,001*10¹⁰	2,331*10^-4	0,102*10^-6
12	1,7	603,71		4,02	6,883*10¹⁰	0,244*10¹⁰	2,413*10^-4	8,111*10^-6
13	1,5	604,29		3,44	7,097*10¹⁰	0,030*10¹⁰	2,340*10^-4	0,828*10^-6
14	1,2	604,96		2,77	7,051*10¹⁰	0,076*10¹⁰	2,355*10^-4	2,359*10^-6
15	1,0	605,42		2,31	7,046*10¹⁰	0,081*10¹⁰	2,357*10^-4	2,529*10^-6
16	0,7	606,12		1,61	7,076*10¹⁰	0,050*10¹⁰	2,347*10^-4	1,509*10^-6
17	0,5	606,62		1,11	7,331*10¹⁰	0,205*10¹⁰	2,265*10^-4	6,654*10^-6
18	0,4	606,85		0,88	7,398*10¹⁰	0,271*10¹⁰	2,245*10^-4	8,695*10^-6
19	0,2	607,27		0,46	7,076*10¹⁰	0,050*10¹⁰	2,347*10^-4	1,509*10^-6
20	0	607,72		0,01
					średni moduł Younga	bład modułu Younga (odch. stand.)	średni współczynnik nachylenia	błąd współczynnika nachylenia
					7,127*10¹⁰	0,186*10¹⁰	2,332*10^-4	6,00*10^-6

Wnioski:

Porównując wyniki z danymi zawartymi w tabeli na stronie 206 w skrypcie Stanisława Szuby można wywnioskować, że badany pręt wykonany był z aluminium. Dość duża wartość odchylenia standardowego wynika z niedokładności pomiarów i zamocowania pręta.