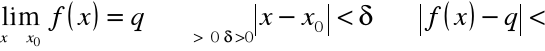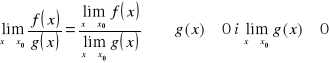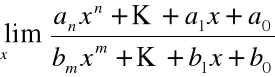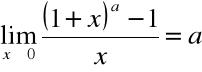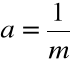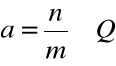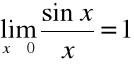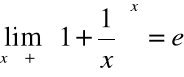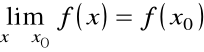WYKŁAD 3

GRANICA FUNKCJI

CIĄGŁOŚĆ FUNKCJI

WŁASNOŚCI FUNKCJI CIĄGŁYCH

Podamy na początku dwie definicje granicy funkcji.

Definicja Heinego (ciągowa)

Dla funkcji i liczba q jest granicą funkcji f w punkcie x0, symbolicznie: lub wtedy i tylko wtedy, gdy dla każdego ciągu jeśli , to

Punkt x₀ może być punktem skończonym

lub punktem w nieskończoności x₀ = ±∝Definicja Cauchy'ego (otoczeniowa)

Liczba q jest granicą funkcji f w x0 wttw: dla każdej liczby ε > 0 istnieje liczba δ > 0 taka, że: jeśli , to

f(x)

x

f(x)

x

Przykład

Udowodnić na podstawie definicji granicy, że:

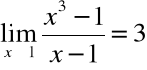
Dowód z definicji Heinego:

Niech
to dowolny ciąg taki, że

Wtedy: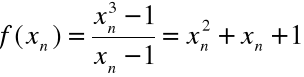

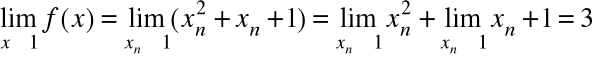
Dowód z definicji Cauchy'ego:

Niech
, i x należy do otoczenia 1 o promieniu 1 tj.

Wtedy: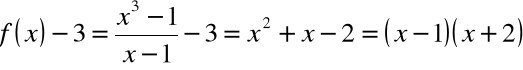

Oraz:

Istnieje zatem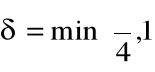
takie, że dla każdego x

z przedziału
zachodzi
,

Stąd, na mocy definicji Cauchy'ego liczba 3 jest granicą f(x) przy

Analogicznie jak dla granic ciągów możemy podać prawa dotyczące obliczania granicy sumy, różnicy, iloczynu i ilorazu funkcji

Twierdzenie (arytmetyka granic funkcji)

Możemy również wprowadzić pojęcie granicy jednostronnej (lewo i prawostronnej)

Wówczas prawdziwe jest twierdzenie o związku między granicą funkcji a granicami jednostronnymi.

Przykład

Rozważmy pewne przypadki:

• n = m

.

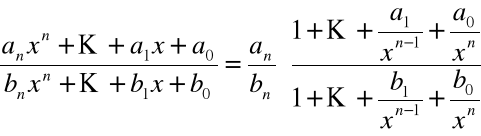
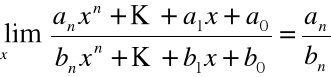
• n < m
  

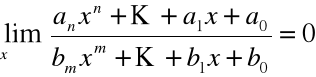
• n > m
  

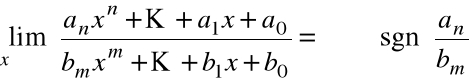
Przykład

Rozważmy kolejno przypadki:

a = n, gdzie n jest liczbą naturalną.

gdzie

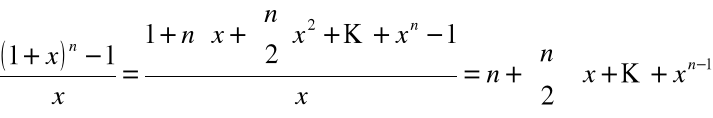
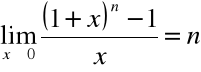
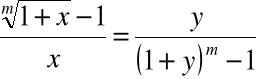
gdzie
;

zatem, ponieważ
gdy

.

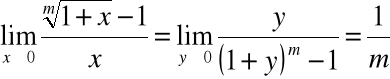
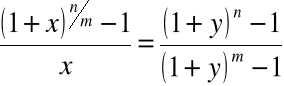
gdzie
,

zatem: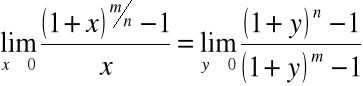
=

=

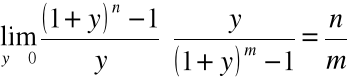
Wybierzmy ciąg
liczb wymiernych
.

Mamy wówczas:

=

=
=
.

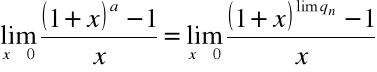
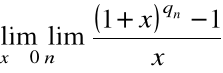
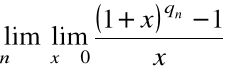
Przykład

Z własności funkcji
dla wartości x bliskich 0 zachodzi:

y y=tgx

y=x

y=sinx

0 x

Stąd: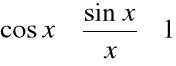
;

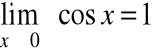
A zatem: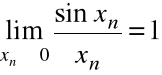
, dla każdego
.

Zatem z definicji ciągowej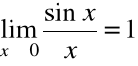

Przykład

Z definicji ciągowej granicy funkcji:

niech ciąg
ciąg taki, że:
.

Dla
, przyjmiemy
tj.
.

Mamy: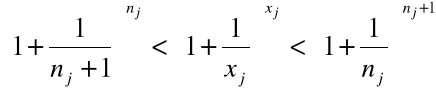
.

Ponieważ: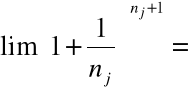

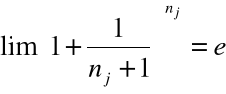
Wnosimy: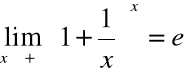
.

Zauważmy, że przyjmując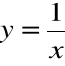
mamy:

Przykład

Skoro zachodzi

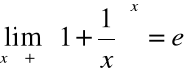
to jest to też prawda dla dowolnego ciągu liczb rzeczywistych (y_n), dążącego do nieskończoności:

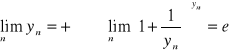
Pokażemy w oparciu o tę własność, że

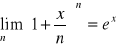
Istotnie:

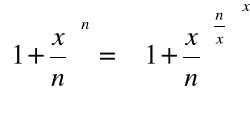
Wystarczy teraz zdefiniować ciąg y_n = x / n

Wtedy: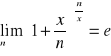

CIĄGŁOŚĆ FUNKCJI

Definicja

Funkcja f(x) jest ciągła w punkcie x0 wttwt

Korzystając z dwóch definicji granicy funkcji otrzymujemy dwie równoważne definicje ciągłości.

Definicja Heinego

Funkcja f(x) jest ciągła w punkcie x0 wttw, jeżeli dla każdego ciągu zbieżnego do , ciąg jest zbieżny do .

Definicja Cauchy'ego

Funkcja f(x) jest ciągła w punkcie x0

Y

y=f(x)

X

Wprost z definicji ciagłości funkcji można wyprowadzić analityczną interpretację ciagłości.

Twierdzenie o wprowadzeniu granicy do argumentu funkcji ciągłej

Jeżeli funkcja f(x) jest ciągła tzn. to wówczas: tzn. operator lim można wprowadzić pod znak funkcji ciągłej

Bezpośrednio z arytmetyki granic funkcji wynika arytmetyka ciagłości funkcji

Arytmetyka ciągłości

Jeżeli: funkcje i są ciągłe w punkcie to wówczas:

Suma + jest funkcją ciągłą w punkcie

Różnica - jest funkcją ciągłą w punkcie

Iloczyn ∙ jest funkcją ciągłą w punkcie

Iloraz jest funkcją ciągłą w punkcie gdy

Twierdzenie o ciągłości funkcji odwrotnej

Funkcja odwrotna do funkcji ciągłej i rosnącej (malejącej) jest ciągła i rosnąca (malejąca).

Przykład

• Funkcja
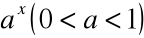
  jest ciągła i malejąca, a więc funkcja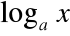
  , odwrotna do niej, jest także ciągła i malejąca.

• Funkcja
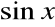
  jest w dziedzinie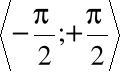
  ciągła i rosnąca, a zatem funkcja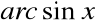
  odwrotna do niej, jest także ciągła i rosnąca.

Twierdzenie o ciągłości funkcji złożonej

Jeżeli: funkcja jest ciągła w punkcie funkcja jest ciągła w punkcie , to: funkcja złożona jest ciągła w punkcie .

Przykład

Funkcja złożona
jest ciągła w każdym punkcie.

Przykład (wykorzystanie ciągłości w liczeniu granic)

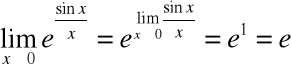
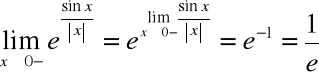
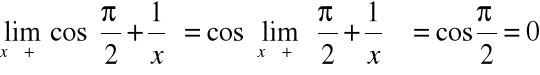
Wykorzystano tutaj ciągłość funkcji
i
.

♦ Ciągłość funkcji elementarnych

• Funkcja stała
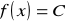
  jest ciągła w każdym punkcie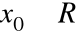
  

• funkcja tożsamościowa
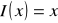
  jest ciągła w każdym punkcie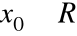
  

Dowód:

Wniosek

Każdy wielomian W
jest funkcją ciągłą dla każdego
.

Przykład

Funkcje:
,

są to funkcje ciągłe w każdym punkcie swej dziedziny naturalnej.

Definicja

Funkcję nazywamy wymierną, jeżeli można ją przedstawić jako iloraz dwóch wielomianów.

Funkcja wymierna jest więc ciągła w każdym punkcie swej dziedziny naturalnej, którą jest zbiór R z wyjątkiem pierwiastków wielomianu znajdującego się w mianowniku.

Przykład (funkcje wymierne ciągłe):

• 
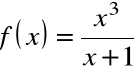
  , jest ciągła dla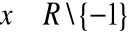
  

• 
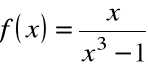
  , jest ciągła dla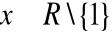
  

• 
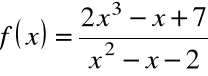
  , jest ciągła dla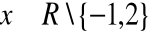
  

Funkcje trygonometryczne:

• 
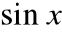
  i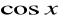
  , są ciągłe dla każdego
  

• 
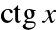
  jest ciągły w zbiorze R\ {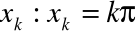
  }

• 
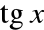
  jest ciągły w zbiorze R \{x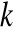
  :
  }

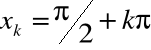
Funkcja wykładnicza

jest ciągła dla każdego
.

Definicja

Funkcja jest ciągła w przedziale otwartym (skończonym lub nieskończonym),

jeżeli jest ciągła w każdym punkcie tego przedziału.

Przykład

• Funkcja
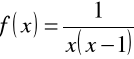
  jest ciągła w przedziałach:

,
i
.

Definicja

Funkcja f(x) jest prawostronnie ciągła w punkcie x₀ jeżeli spełniony jest warunek

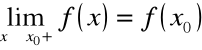
gdzie
oznacza, że x dąży do
z prawej strony.

Funkcja f(x) jest lewostronnie ciągła w punkcie x₀ jeżeli spełniony jest warunek

.

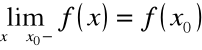
gdzie
oznacza, że x dąży do
z lewej strony.

Przykład

Funkcja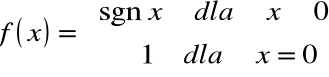

y

1

0 x

-1

jest prawostronnie ciągła w punkcie
ponieważ

natomiast nie jest w tym punkcie lewostronnie ciągła, ponieważ

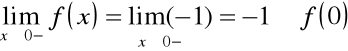
Jeżeli funkcja
jest ciągła w punkcie
, to jest w tym punkcie lewo- i prawostronnie ciągła, a także na odwrót.

Definicja

Funkcja f(x) jest ciągła w przedziale domkniętym [a,b] jeżeli spełnia następujące warunki:

• jest ciągła w przedziale
  

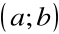
• prawostronnie ciągła w punkcie a,

• lewostronnie ciągła w punkcie b.

Przykład

Funkcja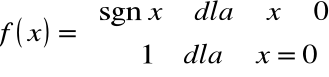

jest ciągła w przedziale

Definicja

Jeżeli funkcja
nie jest ciągła w punkcie
,

to
nazywamy punktem nieciągłości tej funkcji.

Rodzaje nieciągłości

Punkty nieciągłości I rodzaju: istnieją granice jednostronne właściwe Jeżeli w szczególności: To mówimy że funkcja f(x) ma w punkcie nieciągłość usuwalną. Nieciągłość taką można usunąć poprzez przedefiniowanie funkcji.

Punkty nieciągłości II rodzaju: wszystkie pozostałe punkty nieciągłości

Definicja

Skok funkcji f(x) w punkcie
definiujemy jako:

Zadanie

Znajdź skok funkcji

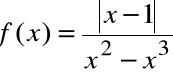
w punkcie nieciągłości.

Rozwiązanie

Otrzymujemy:

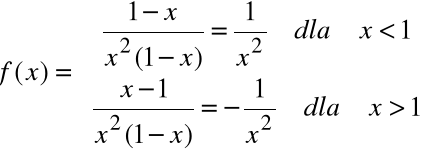
Skoro: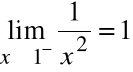

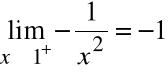
to wartość skoku wynosi:

WŁAŚCIWOŚCI FUNKCJI CIĄGŁYCH

Twierdzenie o lokalnym zachowaniu znaku

Jeżeli: funkcja jest ciągła w punkcie oraz to: istnieje takie otoczenie Q punktu w którym

Jeżeli: funkcja jest ciągła w punkcie oraz to: istnieje takie otoczenie Q punktu w którym

0
x

δ

Przykład

Funkcja
jest ciągła w punkcie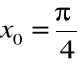

Oraz zauważamy że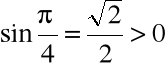
.

Istnieje więc takie otoczenie
, w którym funkcja
zachowuje znak, tzn.
.

Załóżmy, że

(dopuścimy, że wśród a, b, c, d występują
);

Twierdzenie Darboux (o osiąganiu wartości pośrednich)

Jeżeli: jest ciągła na , to: istnieje liczba taka, że u=f(c)

W języku potocznym: Jeśli liczba u jest zawarta między dwiema wartościami funkcji ciągłej f, to liczba u jest też wartością funkcji f ; funkcja ciągła f przyjmuje wszystkie wartości pośrednie między f(a) i f(b)

Inaczej: Funkcja ciągła przekształca przedziały na przedziały

y y=f(x)

f(b)

u= f(z)

f(a)

0 a z b x

Dowód (nie wprost)

Załóżmy, że tak nie jest, wobec tego mamy trójkę

gdzie np.
i
dla

Przyjmijmy:

.

Zbiory A i B są rozłączne i w sumie dają przedział
.

Z zasady zupełności wnosimy o istnieniu kresu górnego

, przy czym

więc istnieje ciąg
taki, że
,

Z ciągłości funkcji f(x) wynika że:

ponieważ
i
, więc istnieje również ciąg
taki, że
, więc
.

Zatem
i z otrzymanej sprzeczności z wyborem u wnosimy, że f ma własność Darboux.

Twierdzenie Weierstrassa (o osiąganiu kresów)

Jeżeli jest ciągła na , To: Istnieją takie, że :

Inaczej: Funkcja ciągła na przedziale domkniętym osiąga na tym przedziale kres górny i kres dolny

y y=f(x)

f(u)

0 a=v

f(v) u b x

Dowód analogiczny jak w poprzednim przypadku .Przykład

Funkcja
jest:

• ciągła w przedziale
  ,

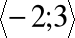
• ograniczona w tym przedziale
  ,

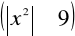
istnieją takie dwa punkty
,

należące do przedziału
, że

,

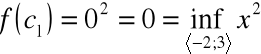
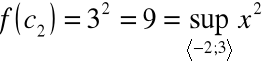
Funkcja ciągła w przedziale domkniętym osiąga

w tym przedziale kres dolny i kres górny zbioru swych wartości.

Funkcja ciągła w przedziale otwartym może nie być ograniczona, a więc kresy zbioru jej wartości w tym przedziale mogą w ogóle nie istnieć.

Taką jest np. funkcja
w przedziale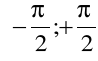
.

Jeżeli nawet funkcja ciągła w przedziale otwartym jest ograniczona, to może nie osiągać w tym przedziale kresu dolnego lub kresu górnego zbioru swych wartości.

Przykład

Funkcja
rozważana w przedziale otwartym
nie osiąga kresu dolnego, ani kresu górnego zbioru swych wartości.

Mamy tu mianowicie

,

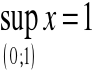
natomiast w żadnym punkcie przedziału
funkcja
nie przyjmuje wartości 0 ani wartości 1.

Funkcja
przyjmuje w przedziale
każdą wartość pośrednią między
i
.

Przykład

Sprawdzić, czy funkcja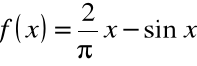
ma

w przedziale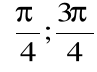
miejsce zerowe.

Funkcja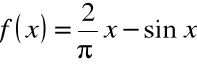
jest ciągła w przedziale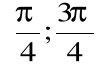
, przy czym

,

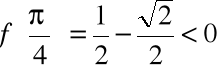
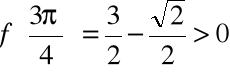
a zatem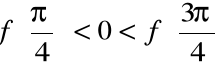
.

Istnieje więc w przedziale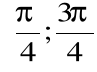

taki punkt c, że
.

Oczywiście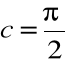
.

Wniosek

Jeżeli: funkcja jest ciągła w przedziale [a,b] , to: istnieje taki punkt , że f(c)=0.

Przykład

Sprawdzić czy funkcja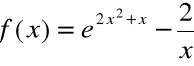
ma miejsce zerowe w przedziale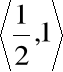
.

Funkcja: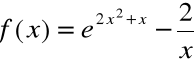

jest ciągła w przedziale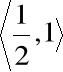

Ponieważ: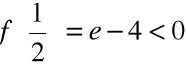
,

Więc: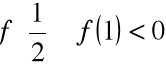

istnieje zatem w przedziale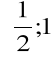
taki punkt c, że

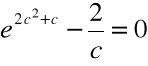
Równanie :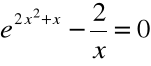

ma więc w przedziale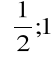
co najmniej jeden pierwiastek.

• WŁASNOŚĆ PUNKTU STAŁEGO

Rozważmy funkcję

Powiemy, że f ma własność punktu stałego,

jeśli istnieje
o tej własności, że:

Punkt
nazywamy punktem stałym funkcji f.

Twierdzenie Brouwera (o punkcie stałym)

Jeżeli: jest funkcją ciągłą na To: f ma własność punktu stałego

Na koniec listy własności funkcji ciągłych podajemy twierdzenie o ciągłości jednostajnej.

Twierdzenie Cantora (o ciągłości jednostajnej)

Jeżeli: funkcja f jest ciągła w przedziale domkniętym [a,b], to: dla każdego istnieje takie , że dla każdych dwóch liczb i przedziału [a,b] takich że zachodzi

Inaczej: Funkcja f(x) jest ciągła na przedziale domkniętym Własność tą nazywamy jednostajną ciągłością funkcji f na [a,b].

Przykład

Funkcja f(x)=sin(2x) jest ciągła w przedziale

Niech:

Ponieważ:

więc:

Y

y=f(x)

0 a x
b X

Przykład

Funkcja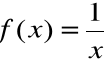
, ciągła na przedziale (0,1) nie jest na tym przedziale jednostajnie ciągła.

Należy wykazać, że:

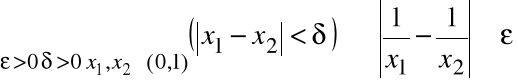
Zdanie to jest prawdziwe,

bo dla
, dowolnego

oraz dla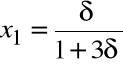
i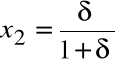

mamy:

oraz:

natomiast: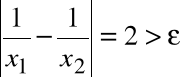

PJWSTK

Analiza Matematyczna 1

22

---