Wydział : |
Imię i nazwisko : Rafał Szuman, Rafał Sikora |
rok II |
Grupa 3 |
Zespół 10 |
||||||
Pracownia fizyczna I |
Temat ćwiczenia : Drgania elektromagnetyczne obwodu RLC |
Ćwiczenie nr: 61 |
||||||||
Data wykonania: 14.03.00 |
Data oddania: 21.03.00 |
Zwrot do poprawy: |
Data oddania: |
Data zaliczenia: |
Ocena: |
|||||
Cel ćwiczenia
Obserwacja drgań tłumionych i przebiegów aperiodycznych w obwodzie LCR. Pomiar i interpretacja parametrów opisujących obserwowane przebiegi napięcia U(t). Badanie obwodu LCR jako modelowej realizacji fizycznej liniowego równania różniczkowego drugiego stopnia.
Wprowadzenie
Zjawisko drgań elektromagnetycznych w obwodzie złożonym z idealnej indukcyjności L i pojemności C jest wyidealizowanym przypadkiem drgań obwodu elektrycznego. Częstość ω takich niegasnących drgań dana jest wzorem
![]()
(1)
Rzeczywisty obwód posiada niezerową rezystancję R, na który składa się rezystancja cewki i dodatkowej opornicy.
Zachowanie obwodu, nazywanego obwodem LCR, opisuje równanie różniczkowe
![]()
(2)
Nie ma łatwego sposobu pomiaru zmiennego w czasie ładunku q(t), ale możemy mierzyć, proporcjonalne do q(t), napięcie kondensatora U(t) = q(t)/C. Równanie powyższe przepisać można dla funkcji U(t) w postaci:
![]()
. (3)
Równanie to, w zależności od wartości wyznacznika
![]()
,
nazwanego rezystancją krytyczną, ma trzy jakościowo różne rozwiązania.
1. Dla wartości R<Rc otrzymujemy rozwiązanie w postaci funkcji
![]()
, (4)
które reprezentuje gasnące drgania kosinusoidalne. β jest współczynnikiem tłumienia, którego odwrotność odpowiada czasowi po którym amplituda sygnału spadnie o czynnik 1/e. Wartości β i ω wyrażają się przez:
![]()
, 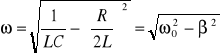
, (4a)
A jest amplitudą niegasnących drgań, a δ jest fazą.
2. Dla wartości R=Rc rozwiązaniem jest funkcja
![]()
, (5)
która ze wszystkich rozwiązań najszybciej maleje do zera (najszybsze wytłumienie drgania),
![]()
. (5a)
3. Dla R>Rc funkcja ma rozwiązanie w postaci
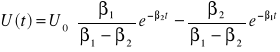
, (6)
gdzie
![]()
, ![]()
. (6a)
Gdy spełnione jest R>>Rc, to powyższą funkcję można przybliżyć funkcją
![]()
, (7)
gdzie τ=RC. Na poniższym rysunku zebrane są wszystkie omówione przypadki.
Opracowanie wyników.
1. Drgania gasnące
W tabeli zebrano wyniki pomiarów dla przebiegu gasnącego.
Rd=0 [Ω]
|
Rd=200 [om] |
||
t [ms] |
U [V] |
t [ms] |
U [V] |
175 |
1,05 |
324,8 |
1,04 |
189,6 |
-0,87 |
339,2 |
-0,78 |
204,8 |
0,65 |
353,6 |
0,54 |
219,2 |
-0,56 |
368 |
-0,41 |
233,6 |
0,39 |
382,4 |
0,26 |
248,8 |
-0,34 |
398,4 |
-0,23 |
263,2 |
0,24 |
412,8 |
0,12 |
277,6 |
-0,23 |
|
|
293,6 |
0,15 |
|
|
308 |
-0,15 |
|
|
321,6 |
0,08 |
|
|
338,4 |
-0,1 |
|
|
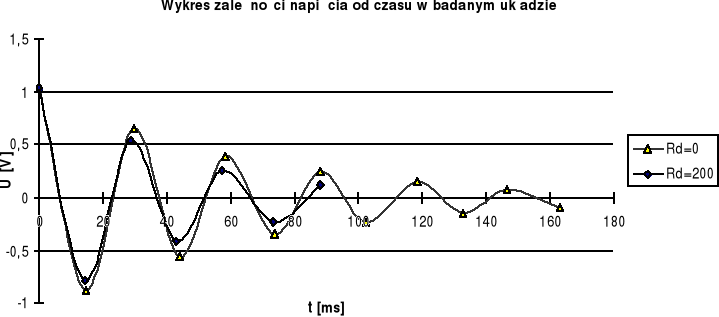
Dane w tabeli poniżej pogrubionej linii nie są brane pod uwagę przy rozważaniach jakościowych, ponieważ ujawnia się tu niedokładność użytego oscyloskopu. Objawia się to podawaniem zawyżonych wartości mierzonego napięcia, szczególnie dla napięć ujemnych. Widać to wyraźnie na poniższym wykresie jako rozrzut punktów o większym t od prostej.
Na podstawie danych z tabeli obliczono okres jako:
![]()
,
gdzie t oznacza czas kolejnego ekstremum, a n i m jego numer. Uzyskano wynik
T= 29,32±0,1 [ms], ![]()
≈214[Hz]. Za błąd pomiaru okresu przyjęto najmniejszą działkę czasu, a błąd częstości pominięto ze względu na jego bardzo małą wartość. Następnie obliczono ln|Ui| i narysowano wykres zależności |ln|Ui|| od t. Dla poprawienia czytelności wykresu przesunięto pierwszy punkt wykresu do wartości t=0.
Rd=0 [Ω] |
Rd=200 [om] |
||
t [ms] |
|ln|U|| [V] |
t [ms] |
|ln|U|| [V] |
0 |
0,048790 |
0 |
0,039221 |
14,6 |
0,139262 |
14,4 |
0,248461 |
29,8 |
0,430783 |
28,8 |
0,616186 |
44,2 |
0,579818 |
43,2 |
0,891598 |
58,6 |
0,941609 |
57,6 |
1,347074 |
73,8 |
1,078810 |
73,6 |
1,469676 |
88,2 |
1,427116 |
88 |
2,120264 |
102,6 |
1,469676 |
|
|
118,6 |
1,897120 |
|
|
133,0 |
1,897120 |
|
|
146,6 |
2,525729 |
|
|
163,4 |
2,302585 |
|
|
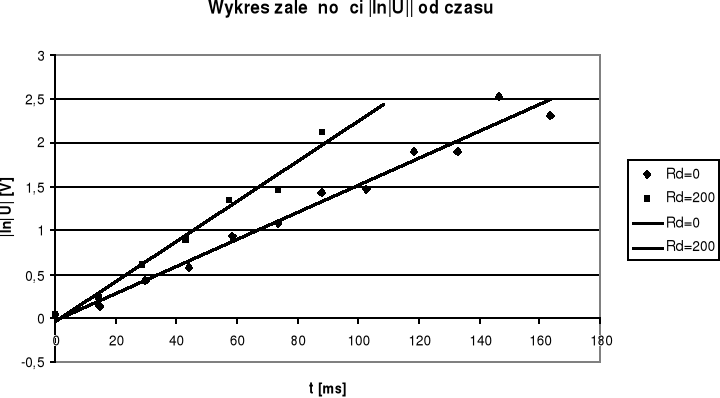
Proste (y=ax+b)są prostymi dopasowanymi metodą najmniejszych kwadratów. Współczynnik nachylenia a jest współczynnikiem tłumienia β. Do obliczeń użyto wzorów:
![]()
,
![]()
,
![]()
,
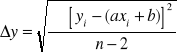
,
![]()
, (8)
Stąd otrzymano wynik (po zamianie ms na s) β=15,4±0,8 dla obwodu bez dodatkowej rezystancji i β=23,0±1,1 dla obwodu z rezystancją Rd=200 Ω.
2. Przebieg aperiodyczny
W tabelce zebrano wyniki pomiarów dla przebiegów aperiodycznych i dane przygotowane do wyrysowania wykresu.
R=Rc=8 [kΩ] |
Rc<<R=15 [kΩ] |
||||||
t [ms] |
U [V] |
t [ms] |
U [V] |
||||
26,48 |
0,66 |
20,8 |
0,67 |
||||
26,64 |
0,66 |
21,6 |
0,66 |
||||
26,8 |
0,66 |
24 |
0,62 |
||||
26,82 |
0,65 |
28 |
0,58 |
||||
27,52 |
0,63 |
34,4 |
0,52 |
||||
28,4 |
0,61 |
38,4 |
0,49 |
||||
29,2 |
0,57 |
42,4 |
0,45 |
||||
29,76 |
0,54 |
50,4 |
0,4 |
||||
31,36 |
0,44 |
58,4 |
0,37 |
||||
33,2 |
0,33 |
66,4 |
0,34 |
||||
34,64 |
0,26 |
80,8 |
0,28 |
||||
36,4 |
0,16 |
96 |
0,24 |
||||
37,12 |
0,14 |
121,6 |
0,19 |
||||
38,96 |
0,08 |
132,8 |
0,17 |
||||
41,12 |
0,04 |
164,8 |
0,13 |
||||
42,56 |
0,01 |
208 |
0,09 |
||||
43,63 |
0 |
272,8 |
0,05 |
||||
|
|
464 |
0,01 |
||||
|
|
464,4 |
0 |
||||
Rc<<R=15 [kΩ] |
R=Rc=8 [kΩ] |
||||||
t [ms] |
|lnU| [V] |
t [ms] |
|lnU| [V] |
||||
0 |
0,400478 |
0 |
0,415515 |
||||
0,8 |
0,415515 |
0,16 |
0,415515 |
||||
3,2 |
0,478036 |
0,32 |
0,415515 |
||||
7,2 |
0,544727 |
0,34 |
0,430783 |
||||
13,6 |
0,653926 |
1,04 |
0,462035 |
||||
17,6 |
0,71335 |
1,92 |
0,494296 |
||||
21,6 |
0,798508 |
2,72 |
0,562119 |
||||
29,6 |
0,916291 |
3,28 |
0,616186 |
||||
37,6 |
0,994252 |
4,88 |
0,820981 |
||||
45,6 |
1,07881 |
6,72 |
1,108663 |
||||
60 |
1,272966 |
8,16 |
1,347074 |
||||
75,2 |
1,427116 |
9,92 |
1,832581 |
||||
100,8 |
1,660731 |
10,64 |
1,966113 |
||||
112 |
1,771957 |
12,48 |
2,525729 |
||||
144 |
2,040221 |
14,64 |
3,218876 |
||||
187,2 |
2,407946 |
16,08 |
4,60517 |
||||
252 |
2,995732 |
|
|
||||
443,2 |
4,60517 |
|
|
||||
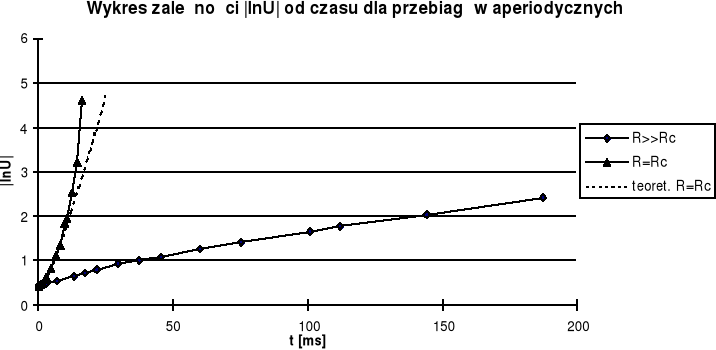
Dla przebiegu aperiodycznego R>>Rc rozwiązanie jest sumą dwóch funkcji wykładniczych (6), przy czym składnik z mniejszą wartością β zanika wolniej. Znajduje to odbicie w wyniku eksperymentu, gdyż wykres początkowo nie jest prostą, przechodzi w nią dopiero dla większych t. Stąd współczynnik nachylenia prostej, liczony analogicznie jak w przypadku 1, jest współczynnikiem β2 równania (6). Wartość tego współczynnika liczono na podstawie wzorów (8) wynosi β2=0,0095±0,0005, przy czym w obliczeniach pominięto pierwszych 7 punktów.
Krzywą teoretyczną dla R=Rc liczono na podstawie wzoru (5), wstawiając ![]()
, U0=0,67 [V] i przyjmując czas z przedziału 0 do 25 [ms]. Wyliczone wartości zestawiono w tabelce.
t [ms] |
U [V] |
t [ms] |
U [V] |
0 |
0,6 |
13 |
0,098874 |
1 |
0,584101 |
14 |
0,081533 |
2 |
0,545878 |
15 |
0,067026 |
3 |
0,495985 |
16 |
0,054947 |
4 |
0,441455 |
17 |
0,044932 |
5 |
0,386781 |
18 |
0,03666 |
6 |
0,334695 |
19 |
0,029848 |
7 |
0,286727 |
20 |
0,024257 |
8 |
0,243604 |
21 |
0,019678 |
9 |
0,205528 |
22 |
0,015938 |
10 |
0,172378 |
23 |
0,01289 |
11 |
0,143838 |
24 |
0,010411 |
12 |
0,119489 |
25 |
0,008397 |
Teoretycznie wyliczone wartości β, ω i β2, obliczone wg. wzorów (1), (4a), (5a) i (6a) wynoszą odpowiednio:
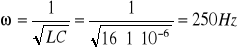
![]()
![]()
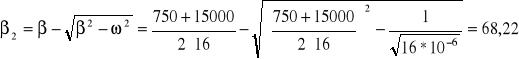
W tabelce zestawiono wartości eksperymentalne i teoretyczne.
|
Teoretycznie |
Eksperymentalnie |
ω |
250 |
214 |
βRd=0 |
23,4375 |
15,4 |
βRd=200 |
29,6875 |
23,0 |
β2 |
68,22 |
9,53 |
Zaskakująco duży błąd dla parametru β2 wziął się prawdopodobnie z mylnego odczytania wartości rezystora dodatkowego. Gdy podstawimy zamiast R=10.000 Ω wartość R=100.000 Ω, otrzymamy wartość β2=9,94, co znacznie lepiej pokrywa się z wynikiem eksperymentu.
Wnioski:
Wyniku eksperymentu w znacznym stopniu pokrywają się z oczekiwaniami teoretycznymi. Trudno jednoznacznie ocenić w jakim stopniu, ponieważ nie posiadaliśmy danych o błędach pomiarów indukcyjności, pojemności i rezystancji cewki. Podane wartości są „okrągłe”, co upraszcza obliczenia, ale może być źródłem rozbieżności. Tezę tą potwierdza pomiar częstości, który był bardzo dokładny, a dał inny niż teoretyczny wynik. Podsumowując, eksperyment w zadowalającym stopniu potwierdził słuszność teoretycznych rozważań.
Wyszukiwarka
Podobne podstrony:
113MOJA, Ochrona Środowiska pliki uczelniane, Fizyka
cw 3, Ochrona Środowiska pliki uczelniane, Fizyka
zgapy z fizyki, Ochrona Środowiska pliki uczelniane, Fizyka
LAB25, Ochrona Środowiska pliki uczelniane, Fizyka
NASZA52, Ochrona Środowiska pliki uczelniane, Fizyka
Lab82b, Ochrona Środowiska pliki uczelniane, Fizyka
Energia wodna na Fizykę, Ochrona Środowiska pliki uczelniane, Fizyka
61-obliczenia2, Ochrona Środowiska pliki uczelniane, Fizyka
113A, Ochrona Środowiska pliki uczelniane, Fizyka
nasza 9, Ochrona Środowiska pliki uczelniane, Fizyka
ENERGIA WODNA1, Ochrona Środowiska pliki uczelniane, Fizyka
Lab61, Ochrona Środowiska pliki uczelniane, Fizyka
NASZA51, Ochrona Środowiska pliki uczelniane, Fizyka
LAB51, Ochrona Środowiska pliki uczelniane, Fizyka
Pobieranie, Ochrona Środowiska pliki uczelniane, Fizyka
sprawozdanie 4 fizyka, Ochrona Środowiska pliki uczelniane, Fizyka
82MOJE, Ochrona Środowiska pliki uczelniane, Fizyka
lab121 wyn, Ochrona Środowiska pliki uczelniane, Fizyka
więcej podobnych podstron