POLITECHNIKA ŚLĄSKA W GLIWICACH

Wydział Elektryczny

Kierunek Mechatronika

Inżynierskie, stacjonarne, sem. 3

LABORATORIUM
PODSTAWY AUTOMATYKI

Temat ćwiczenia: Regulacja PID

Sekcja 2:

Gowik Mariusz

Kasprowicz Przemysław

Gliwice 2014

1. Wprowadzenie

Celem ćwiczenia było dla danej transmitancji dobrać regulatory P, PI i PID wraz z ich nastawami w układzie zamkniętym z sprzężeniem zwrotnym.

Rys. 1 Schemat ogólny układu

2. Przebieg ćwiczenia

Nasz obiekt jest opisany następującą transmitancją

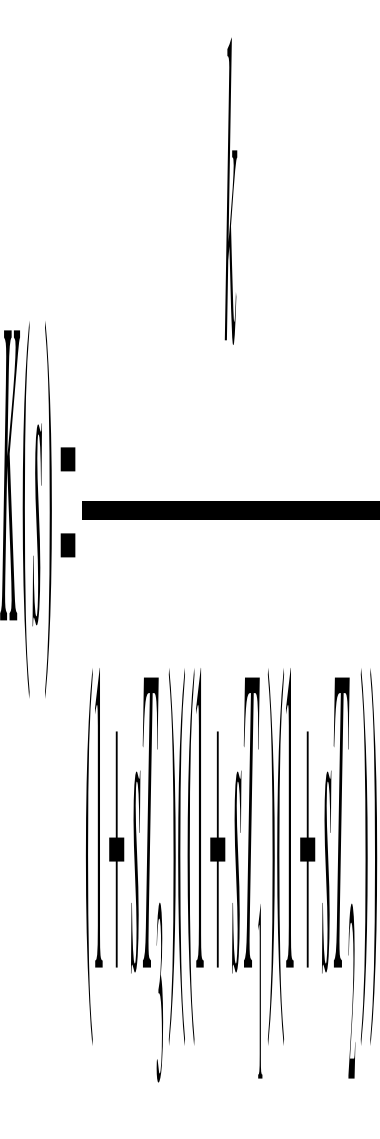
nasze dane to:

k=1

T₁=2

T₂=3

T₃=0,4

Po podstawieniu danych otrzymujemy nastepujące wyniki

Nastawy regulatorów otrzymaliśmy używając metody QDR. Na początku musimy ustalić dwie stałe czasowe dla 63,2% i 28,3% odpowiedzi dla stanu ustalonego co uzyskaliśmy korzystając z funkcji step().

Wykres 1 Odpowiedż skokowa układu bez regulatorów.

Odczytując z wykresu te dwie wartości możemy przesjść do wyliczenia stałej czasowej inercji 1 rzędu T i czasu opóżnienia T₀.

t₁=5,789

t₂=3,039

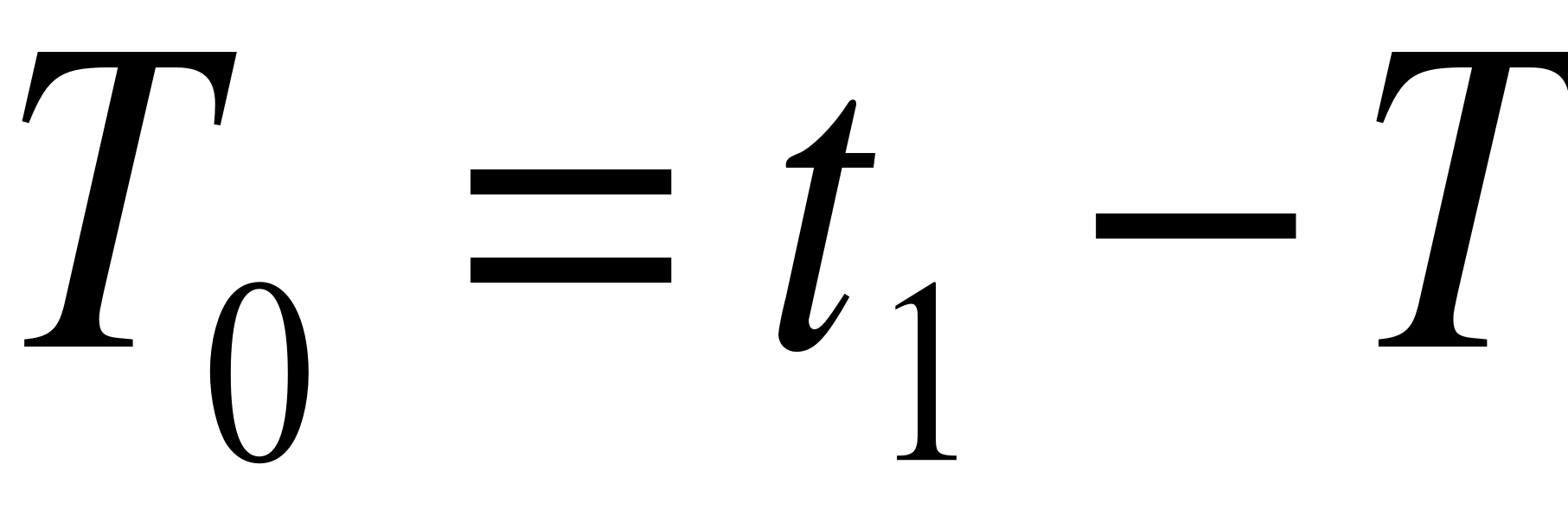
T=4,125

T₀=1.665

Kolejną rzeczą jest sprawdzenie warunku niekontrolowalności

0,15<T0/T<0,6

Który dla naszego przypadku wynosji 0,4034 wiec warunek jest spełniony, więc możemy zacząć liczyć nastawy regulatorów.

1. Regulator typu P.

Wzór na wzmocnienie jest następujący:

k_r=T/(k*T0)

I otrzymujemy wartość k_r= 2,479.

Transmitancja regulatora typu P wynosi:

G(s)=k_r

2. Regulator typu PI.

Wzmocnienie wyznaczamy wzorem:

k_r=(0,9*T)/(k*T0)

Nasz wynik to k_r= 2,231 , natomiast stałą czasową T_i wyznaczamy z wzoru:

T_i=3,33*T₀

T_i=5,541

Transmitancja tego regulatora przedstawia się następująco:

G(s)=k_r(1+(1/T_i*s))

G(s)=0.4026 s + 2.231

3. Regulator typu PID.

Wzocnienie:

k_r=(1,2*T)/(k*T0)

k_r=2,9748

Stała czasowe T_i

T_i=2*T₀

T_i=3,328

Stała czasowa T_d

T_d=T₀/2

T_d=0,832

Stała czasowa T_D

T_D=0,02*T_d

T_D=0,0166

Transmitancja tego regulatora opisana jest wzorem:

G(s)=k_r(1+(1/T_i*s)+((T_D*s)/(1+T_d*s)))

G(s)=(8.402*s^2+12.37*s+2.975)/(2.769*s^2+3.328*s)

Gdy posiadamy już transmitancje poszczególnych regulatorów możemy zacząć liczyć transmitancję układu otwartego i zamkniętego uchyb, zapas amplitudy i fazy oraz przeregulowanie dla każdego z nich. Dla układu otwartego jest to łatwa sprawa gdyż wystarczy iloczyn transmitancji obiektu i regulatora.

Poniżej przedstawiono wyniki transmitancji układu otwartego z poszczególnymi regulatorami.

Regulator P

Regulator PI

Regulator PID

Dla układów zamkniętych by obliczyć transmitancję musimy skorzystać z wzoru

K=(K*G)/(1+K*G)

Po podstawieniu danych otrzymujemy następujące wyniki:

Regulator P

Regulator PI

Regulator PID

Gdy posiadamy już transmitancję możemy wyliczyć uchyby z wzory:

Uchyb=1-Kzmakniety

Ponizej przedstawiono uchyb dla poszczególnych regulatorów w postaci wykresu dla odpowiedzi skokowej wykorzystując funkcję step().

Regulator P

Regulator PI

Regulator PID

Maksymalne przeregulowanie i czas opóźnienia narastania regulacji zostaly wykonane funkcja step() na układzie zamkniętym z pętlą zwrotną w celu porównania regulatorów zostały nałożone na jeden wykres.

Zapas amplitudy i fazy został wykonany na układzie otwartym funkcja nyquist(), również tutaj w celu porównania wykresy zostały nałożone dla siebie.

Wskaźnika nadążania został utworzony funkcją bodemag() z układów zamkniętych i równierz w celu porównania nałożono na siebie poszczególne wyniki.

3. Wnioski

Zauważyć można że regulatory typu P służą jedynie do wzmacniania sygnału wejsciowego gdzie regulatory typu PI lub PID ten sygnał dodatkowo poddają obrubce zwiększając lub zmniejszając zapasy fazy lub przeregulowanie układu. Zauważyć też można iż regulator PID przy odpowiednich nastawach może służyć jako regulator P, PI lub PD co czyni go bardzo wszechstronnym w urzyciu.

---