Przykład 3.1.

Badano roczne wydatki na remont mieszkania w pewnym mieście i od losowo wybranych 25 mieszkańców otrzymano dane dotyczące ich rodzin zawarte w poniższej tabeli. Na podstawie uzyskanych danych oszacować metodą przedziałową na poziomie ufności
=0,95 przeciętny poziom wydatków na remonty w rodzinach zamieszkałych w tym mieście.

Wydatki na remont mieszkania w roku 2000.

Wydatki (w tys. zł)	x i	0 - 1	1 - 2	2 - 3	3 - 4	4 - 5
Liczba rodzin	n i	3	8	7	5	2

(Dane umowne)

Na podstawie losowo wybranej próby wyznaczamy wartość średnią i odchylenie standardowe wydatków na remont mieszkania. Traktujemy je jako estymatory wartości przeciętnej i odchylenia standardowego wydatków na remont dla populacji generalnej (mieszkańców pewnego miasta).

Na podstawie powyższych obliczeń wynika, że:

tys. zł.,
tys. zł.

Ze względu na małą próbę liczbowy przedział ufności dla wartości średniej wyznaczamy, korzystając ze wzoru:

Ponieważ próba liczyła n = 25 elementów i przyjęliśmy poziom ufności
=0,95, wartość
odczytujemy w tablicach rozkładu Studenta la n - 1 = 24 i
= 0,05.

Otrzymujemy w ten sposób przedział:

=

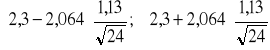
= (2.3 - 0,476; 2,3 + 0,476) = (1,824 tys. zł; 2,776 tys. zł).

Zatem z prawdopodobieństwem 0,95 można stwierdzić, że średnie wydatki na remont mieszkania ponoszone przez mieszkańców pewnego miasta mieszczą się w przedziale między 1,824 tys. zł a 2,776 tys. zł. Maksymalny błąd tego oszacowania
= 476 zł.

Aby ocenić wpływ liczebności próby na precyzję oszacowania, wyznaczmy przedział ufności w poprzednim przykładzie, zakładając, że parametry z próby mają takie same wartości a zmienia się liczebność próby.

Przykład 3.2.

Badając roczne wydatki na remonty w rodzinach pewnego miasta uzyskano dla 10 rodzin: przeciętne wydatki
2,3 tys. zł przy odchyleniu standardowym s = 1,13 tys. zł. Na podstawie powyższych danych oszacować metodą przedziałową na poziomie ufności
=0,95 przeciętny poziom wydatków na remonty w rodzinach zamieszkałych w tym mieście.

Wartość
znajdujemy w tablicach rozkładu Studenta dla n-1=9 i
=0,05. Mamy zatem:
. Podstawiając te wartości do wzoru otrzymujemy:

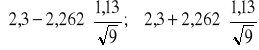
= (2.3 - 0,852; 2,3 + 0,852) = (1,448; 3,152)

Zatem roczne wydatki na remonty w rodzinach mieszkających w tym mieście oszacowane na podstawie 10 elementowej próby zawierają się w przedziale (1,448 tys. zł; 3,152 tys. zł) z prawdopodobieństwem 0,95. Maksymalny błąd tego oszacowania
= 852 zł..

Widać więc, że szacowanie na podstawie mniejszej próby istotnie zwiększyło błąd szacunku.

Rozwiążemy teraz powyższe zadanie dla dużej próby.

Przykład 3.3.

Badając roczne wydatki na remonty w rodzinach pewnego miasta uzyskano dla 625 rodzin: przeciętne wydatki
2,3 tys. zł przy odchyleniu standardowym s = 1,13 tys. zł. Na podstawie zebranych danych oszacować metodą przedziałową na poziomie ufności
=0,95 przeciętny poziom wydatków na remonty w rodzinach zamieszkałych w tym mieście.

W tym przypadku pobrana próba jest duża, zatem zastosujemy wzór:

Wartość
odczytamy w tablicach rozkładu normalnego tak, aby
, tzn. aby F(
)=1 - 0,025 = 0,975. Wtedy
= 1,96. Szukany przedział ufności ma więc postać:

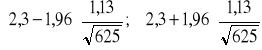
= (2,3 - 0,089; 2,3 + 0,089) = (2,211; 2,389)

Zatem roczne wydatki na remonty w rodzinach mieszkających w tym mieście oszacowane na podstawie 625-elementowej próby zawierają się w przedziale (2,211 tys. zł; 2,389 tys. zł) z prawdopodobieństwem 0,95. Maksymalny błąd tego oszacowania
= 89 zł..

Jak widzimy, szacowanie na podstawie większej próby istotnie zmniejszyło błąd szacunku.

Przykład 3.4.

Sprawdźmy teraz, jak zmieni się precyzja oszacowania, gdy zwiększymy poziom ufności w przykładzie 3.2 przyjmując
= 0,98. Szukamy teraz
tak, aby: F(
)=1-
=1 - 0,01= 0,99. Odczytujemy
= 2,35. Zatem szukany przedział ufności:

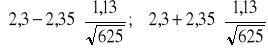
= (2,3 - 0,106; 2,3 + 0,106) = (2,194; 2,406).

Roczne wydatki na remonty w rodzinach mieszkających w tym mieście oszacowane na podstawie 625-elementowej próby zawierają się w przedziale (2,194 tys. zł; 2,406 tys. zł) z prawdopodobieństwem 0,98. Maksymalny błąd tego oszacowania
= 106 zł.

Widać zatem, że zwiększając poziom ufności, zwiększamy również błąd szacunku.

Uwagi:

1. Im krótszy przedział ufności, tym mniejszy błąd szacunku a więc lepsza dokładność oszacowania.

2. Przy ustalonej liczebności próby wraz ze wzrostem poziomu ufności rośnie rozpiętość przedziału ufności czyli maleje dokładność oszacowania.

3. Przy zadanym poziomie ufności im większa jest liczebność próby, tym krótszy przedział ufności czyli lepsza precyzja oszacowania

Przykład 3.5.

Oszacować metodą przedziałową, jaki procent mieszkańców miasta M nie korzysta z usług zakładów fryzjerskich, jeśli wśród 350 osób o to zapytanych 245 oświadczyło, że nie chodzi do fryzjera. Przyjąć poziom ufności (1 -
) =0,99.

Niech p oznacza procent osób w tym mieście nie korzystających z usług zakładów fryzjerskich.

Z podanych informacji wynika, że dla próby o liczebności n = 350 osób wyróżniony wariant cechy (nie korzysta z usług fryzjera) posiada k = 245 osób. Dla (1-
) =0,99 mamy
. W tablicach rozkładu normalnego odczytujemy F(2,59) = 0,995. Do obliczeń przyjmijmy
= 2,6

Zgodnie ze wzorem mamy:

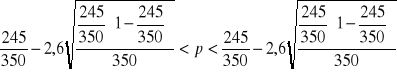
Po wykonaniu obliczeń otrzymujemy 0,58 < p < 0,82.

Zatem z prawdopodobieństwem 0,99 możemy twierdzić, że od 58% do 82% mieszkańców tego miasta nie chodzi do fryzjera .

Maksymalny błąd oszacowania wynosi 0,5(82% - 58%) = 12%.

Przykład 3.6.

Jak liczna powinna być próba, aby dla poprzedniego przykładu maksymalny błąd oszacowania, na poziomie ufności (1-
) =0,99, nie przekraczał 5%:

1. przy założeniu, że z wstępnej próby otrzymaliśmy p=0,68 (to założenie jest zgodne z danymi przykładu),

2. gdy nie znamy rzędu wielkości szacowanego wskaźnika struktury.

Rozwiązanie (a). Mamy do czynienia z sytuacją (1).

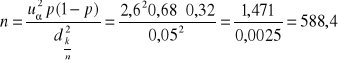
W tej sytuacji maksymalny błąd oszacowania nie przekraczający 5% uzyskamy biorąc próbę 589 osób.

Rozwiązanie (b) Mamy do czynienia z sytuacją (2).

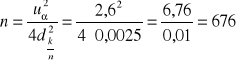
W tej sytuacji należy przyjąć, że oczekiwaną dokładność oszacowania uzyskamy biorąc próbę o liczebności n = 676 osób.

---