1.8 Wymiarowanie.

1.8.1 Charakterystyki materiałowe.

Przyjęto:

Beton B40

R_b = 23.1 MPa E_b = 36.4 MPa

Stal A-II 18G2A

R_a = 295 MPa E_a = 210GPa

n = E_a/E_b n = 5.77

1.8.2 Sprawdzenie czy przekrój jest teowy.

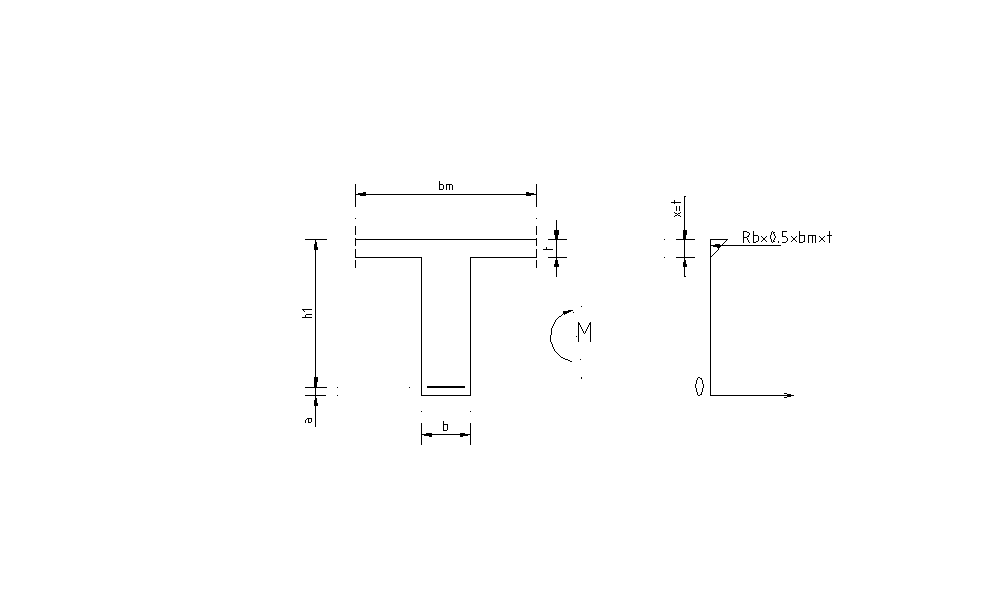
Wyznaczenie szerokości współpracującej:

t/h = 0.21/1.61 = 0.13 -stosunek grubości płyty do całkowitej wysokości żebra łącznie z płytą

b₁ =1.36m -całkowity wysięg wspornika

b₂ = 1.61m -połowa rozpiętości w świetle płyty

a=0.1m -otulina

l = 0.8⋅l_t = 0.8⋅32.20 = 25.76m

b₂/l = 1.61/25.76 = 0.062

wg PN-91/S-10042, tabela 10 odczytano

λ = 1.00

b_m1 = λ⋅b₁ = 1⋅1.36 = 1.36

b_m2 = λ⋅b₂ = 1⋅1.61 = 1.61

b_m = b_m1 + b_m2 + b_o

b_m = 1.36 + 1.61 +0.5 = 3.47m

Z warunku sumy momentów względem punktu „0” wynika ,że:

M_p = (R_b⋅t⋅0.5⋅b_m)⋅(h₁ - t/3)

M_p = 12219.73 kNm

M_p > M_prz.max = 8114.8 kNm - przekrój pozornie teowy

1.8.3 Obliczenie zbrojenia głównego.

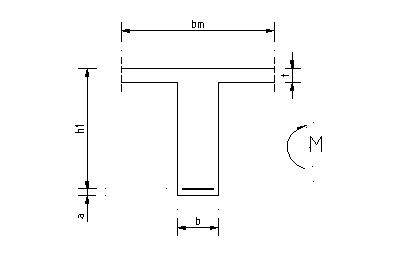
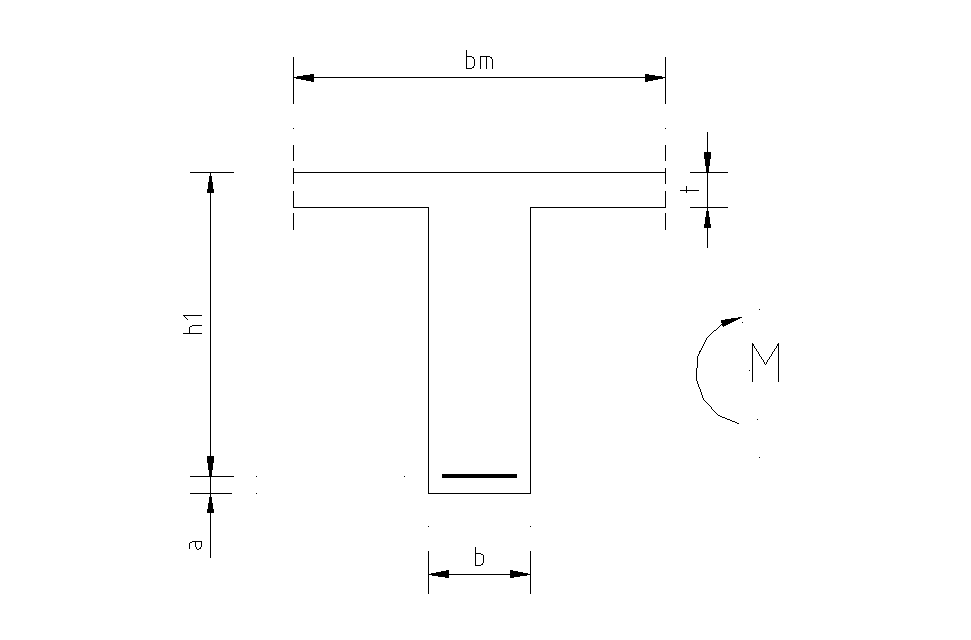
M=8114.8 kN m -maksymalny moment w przęśle

b=0.50m -szerokość żebra

t=0.21m -wysokość płyty

b_m=3.47m -szerokość współpracująca płyty

h₁=1.56m -wysokość użyteczna przekroju

a=0.05m -otulina

w_z = n⋅ M /(R_a⋅b_m⋅h₁²)

w_z=5.77⋅8114.8/295000⋅3.47⋅1.56²=0.018

z [3] tablicy 35 odczytano:

m₁ = 0.216

m_z = 0.941

m_x=0.177

x=m_x⋅h₁

x=0.276m>t=0.21m -przekrój rzeczywiście teowy

Pole zbrojenia

z=h₁-0.5t

z=1.455m

F_a=M/R_a⋅z

F_a=8114.8/295⋅1.455=182.7cm²

Przyjęto zbrojenie 23 φ 32mm

A_a=184.96cm²

Sprawdzenie naprężeń

A₁=((b_m-b)⋅t+n⋅A_a)/b

A₁=((3.47-0.5)⋅0.21+5.77⋅184.96⋅10^-4)/0.5

A₁=1.45m

B₁=((b_m-b)⋅t²+2n⋅A_a⋅h₁)/b

B₁=((3.47-0.5)⋅0.21²+2⋅5.77⋅184.96⋅10^-4⋅1.56)/0.5

B₁=0.92m²

x=
-A₁

x=0.28m

J=((b_m⋅x³) -(b_m-b) ⋅(x-t)³)/3+n⋅A_a⋅(h₁-x)²

J=((3.47⋅0.28³)-(3.47-0.5)(0.28-0.21)³)/3+5.77⋅184.96⋅10^-4⋅(1.56-0.28)²

J=(0.076-0.001018)/3+0.174=0.236m⁴

σ_b = M ⋅x/J

σ_b = 8114.8⋅0.28/0.236

σ_b = 9.627 MPa<R_b=23.1MPa

σ_a = (n⋅M/J)⋅(h₁-x)

σ_a =(5.77⋅8114.9/0.236) ⋅(1.56-0.28)

σ_a =253.55MPa<R_a=295.00MPa

Moment przenoszony przez zbrojenie

M_z=A_a⋅R_a⋅z

M_z=184.96⋅10^-4⋅295⋅10³⋅1.455

M_z=7938.94 kNm

Gęstość zbrojenia

μ = A_a/2⋅0.5+0.21⋅3.47

μ =0.0107> μ_min=0.004 -warunek spełniony

1.8.4 Obliczenie długości zakotwienia.

d=32mm -średnica pręta

R_p=3.9MPa -obliczeniowa przyczepność pręta do betonu

I_bo=d⋅R_a/4⋅R_p

I_bo=0.61m -podstawowa długość kotwienia

δ=1.0 -współczynnik wg.tabl.21[2]

A_aobl=182.7cm²

A_arzecz=184.96cm²

I_b=δ⋅I_bo⋅A_aobl/A_arzecz

I_b=0.60m

I_bmin≥I_b

I_bmin=25⋅d I_bmin=0.80m

Przyjęto długość zakotwienia I=0.80m

1.8.5 Obliczenia zbrojenia na ścinanie.

τ_R=0.35MPa -naprężenia ścinające w betonie B40

R_aw=295.00MPa -wytrzymałość obliczeniowa strzemion (stal AII)

R_a=295.00MPa -wytrzymałość obliczeniowa prętów odgiętych

1.8.6 Wyznaczenie sił miarodajnych.

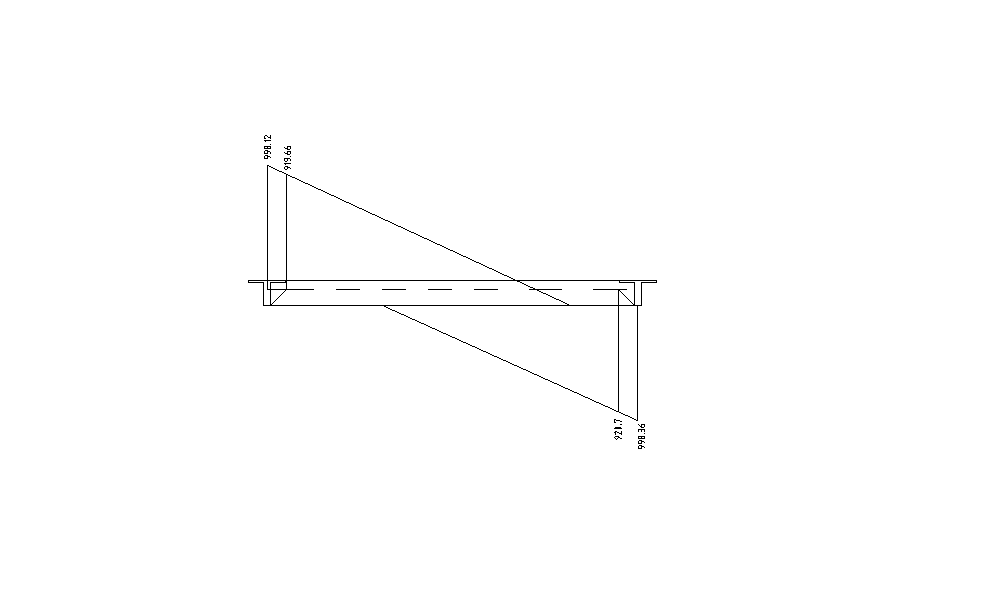
V_s1=920.7kN

1.8.7 Obliczenie zbrojenie na podporze z prawej strony.

1.8.7.1 Odcinek z prętami odgiętymi i strzemionami.

μ =0.0107 -gęstość zbrojenia rozciąganego

b=0.50m -szerokość żebra

z=0.85⋅h₁

z=1.32m -ramię sił wewnętrznych

Elementy niezbrojone na ścinanie.

τ=V_s1/b⋅z

τ=1.39MPa τ=0.35MPa

Ponieważ przekrój jest zbrojony podłużnie wytrzymałość betonu na ścinanie ulega zwiększeniu

A_a=184.96cm²

μ =A_a/b⋅h₁

μ =0.0107

1+50⋅ μ=1.53

τ_R⋅1.53=0.53MPa 0.53MPa<1.39MPa

Przekrój należy zbroić na ścinanie.

Siła przenoszona przez sam beton

V_b=τ_R⋅(1+50⋅ μ)⋅b⋅z

V_b=190.88 kN

Siła przenoszona przez pręty odgięte

V_a=2⋅R_a⋅π(32mm)²/4⋅sin(45deg)

V_a=335.52 kN

Siła jaką powinny przenosić strzemiona

V_W=V_s1-V_b-V_a

V_w=394.30 kN

Maksymalny rozstaw stzremion

Przyjęto strzemiona czterocięte φ 12 o A_aw=4.52cm²

S=A_aw⋅z⋅R_aw/V_w

S=0.44m

Na odcinku gdzie występują prety odgięte przyjęto rozstaw strzemion co 30cm

Gestość zbrojenia strzemionami

μ_w=A_aw/s⋅b

μ_w=0.00301 0.00301≥μ_wmin μ_wmin=0.0030

Na odcinku gdzie występują pręty odgięte przyjęto strzemiona co 30cm

1.8.7.2 Odcinek bez pretów odgiętych.

Siła przenoszona przez strzemiona

V_b=394..30 kN

z=1.32m

b=0.5m

Siła przenoszona przez strzemiona

V_w=899.30 - 394.30

V_w=505.00 kN

Maksymalny rozstaw strzemion

S=A_aw⋅z⋅R_aw/V_w

S=34.85 cm

Przyjmuję rozstaw strzemion co 30cm

μ_w=A_aw/s⋅b

μ_w=0. 0030 = 0.0030=μ_wmin μ_wmin=0.0030

---