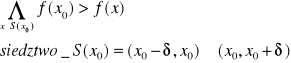Temat 39 Asymptoty wykresu funkcji, wzory na pochodne, pochodna a monotoniczność funkcji

Asymptota pionowa

Asymptota pionowa istnieje w punktach nie należących do dziedziny, a więc nie może być przecięta

a) Prosta x = a jest asymptotą pionową lewostronną krzywej y=f(x) , jeżeli

albo

b) Prosta x = a jest asymptotą pionową prawostronną krzywej y=f(x) , jeżeli:

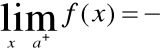
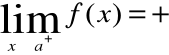
albo

c) Prosta x = a jest asymptotą pionową obustronną krzywej y=f(x) , jeżeli: jest ona asymptotą pionową lewostronną i prawostronną krzywej .

Asymptota ukośna

Wykres może posiadać najwyżej dwie asymptoty ukośne. Jest ona w postaci y=ax+b gdzie

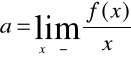
w przypadku granicy lewostronnej

oraz w przypadku granicy prawostronnej

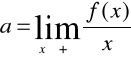
Asymptota ukośna może być przecięta przez wykres.

(warto zapamiętać - funkcja wymierna posiada asymptotę ukośną gdy najwyższa potęga licznika jest o 1 większa od najwyższej potęgi mianownika)

Szczególnym przypadkiem asymptoty ukośnej jest asymptota pozioma.

Asymptota pozioma

Asymptota pozioma (prawo lub/i lewostronna) istnieje wówczas gdy granica funkcji w nieskończoności (+ lub/i -) jest skończona.

(warto zapamiętać - funkcja wymierna posiada asymptotę poziomą gdy najwyższa potęga licznika i mianownika jest równa)

|

|

v

ciąg dalszy na następnej stronie

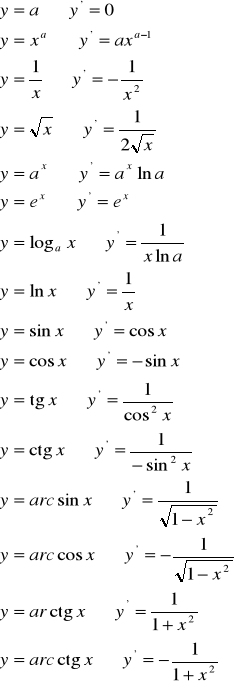
Wzory na pochodne

Pochodna a monotoniczność

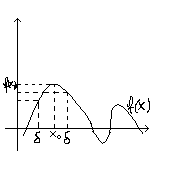
Funkcja posiada w punkcie x₀ maksimum lokalne jeżeli w dowolnym sąsiedztwie punktu x₀ przyjmuje wartości mniejsze od x₀

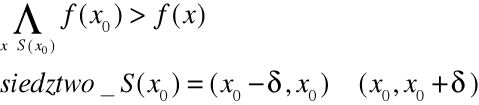
Styczna do maksimum (minimum) musi być równoległa do osi OX

y=0x+b

Warunek Konieczny Istnienia Ekstremum Funkcji w Punkcie

Jeżeli funkcja f jest różniczkowalna w punkcie x₀ i posiada w tym punkcie ekstremum to pochodna funkcji w tym punkcie jest równa 0

Warunkiem koniecznym istnienia ekstremum funkcji różniczkowalnej w punkcie jest to aby pochodna funkcji w tym punkcie była równa 0

Warunek wystarczający istnienia ekstremum funkcji

Jeżeli funkcja f jest określona i różniczkowalna w przedziale (a;b) i i w punkcie x₀ spełniony jest warunek konieczny oraz w przedziale

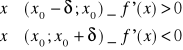
to w punkcie x₀ jest maksimum lokalne funkcji f

Jeżeli funkcja f jest określona i różniczkowalna w przedziale (a;b) i i w punkcie x₀ spełniony jest warunek konieczny oraz w przedziale

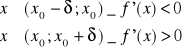
to w punkcie x₀ jest minimum lokalne funkcji f

Jeżeli w punkcie x₀ spełniony jest warunek konieczny, ale w otoczeniu punktu x₀ nie następuje zmiana znaku pochodnej to w tym punkcie nie ma ekstremum

Wystarczy aby funkcja była określona w przedziale (a,b) i różniczkowalna z wyjątkiem punktu x₀ , to wtedy jeżeli spełniony jest warunek wystarczający to funkcja posiada w tym punkcie ekstremum.

Druga pochodna a ekstrema

Jeżeli funkcja f spełnia następujące założenia:

-ma drugą pochodną f ''(x) w pewnym otoczeniu U(x₀ ;δ)

-f ''(x) jest ciągła w punkcie x₀

-f '(x₀)=0 i f `'(x₀)≠0

to funkcja ma w punkcie x₀ :

-minimum lokalne, gdy f `'(x₀)>0

-maksimum lokalne, gdy f `'(x₀)<0

Twierdzenia dotyczące związku między pochodną funkcji, a jej monotonicznością

1. Jeżeli funkcja f jest określona i różniczkowalna w przedziale (a;b) i pochodna funkcji w tym przedziale jest dodatnia to funkcja jest rosnąca

2. Jeżeli funkcja f jest określona i różniczkowalna w przedziale (a;b) i pochodna funkcji w tym przedziale jest ujemna to funkcja jest malejąca

3. Jeżeli funkcja f jest określona i różniczkowalna w przedziale (a;b) i funkcja w tym przedziale jest rosnąca to pochodna funkcji jest nieujemna

4. Jeżeli funkcja f jest określona i różniczkowalna w przedziale (a;b) i funkcja w tym przedziale jest malejąca to pochodna funkcji jest niedodatnia

5. Jeżeli funkcja f jest określona i różniczkowalna w przedziale (a;b) i pochodna funkcji w tym punkcie jest nieujemna to funkcja jest niemalejąca

6. Jeżeli funkcja f jest określona i różniczkowalna w przedziale (a;b) i pochodna funkcji w tym przedziale jest niedodatnia to funkcja jest nierosnąca

Sebastian Kujath kl. IVa

Wyszukiwarka