Robert Maniura

Sprawozdanie z ćwiczenia nr B-12: Wyznaczanie objętości nadmiarowych.

1. Wstęp teoretyczny:

Wśród parametrów opisujących stan układu (p, V, T) oraz funkcji termodynamicznych (U, H, S, F, G) można wyróżnić dwie grupy zmiennych. Zmienne przedstawiające intensywne właściwości układu nie zależą od masy zawartej w układzie: są to ciśnienie (p) i temperatura (T). Wielkości należące do drugiej grupy zmiennych (V, U, H, S, F i G) opisują ekstensywne właściwości układu, zależąc od wielkości masy zawartej w układzie. Zmienne intensywne są funkcjami jednorodnymi rzędu zerowego, zaś zmienne ekstensywne są jednorodnymi funkcjami rzędu pierwszego. Homogeniczna funkcja f rzędu n spełnia tzw. teoremat Eulera, według którego:

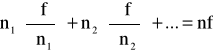
Niech Y oznacza dowolną ekstensywną funkcję termodynamiczną (U, H, S, F, G lub V). W najogólniejszym przypadku będzie ona zależeć od parametrów zewnętrznych (p, T) oraz liczby moli składników (n_i):

Różniczka zupełna tej funkcji ma postać:

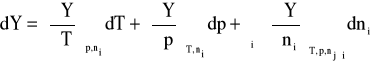
Dla układu dwuskładnikowego, złożonego z rozpuszczalnika i substancji rozpuszczonej, w ustalonych warunkach zewnętrznych (T, p = const) równanie to upraszcza się do postaci:

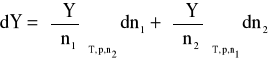
Pochodną cząstkową ekstensywnej funkcji termodynamicznej Y względem liczby moli składnika i przy ustalonych warunkach zewnętrznych oraz liczbach moli pozostałych składników nazywamy cząstkową wielkością molową danego składnika i oznaczamy przez
.

Cząstkowe molowe funkcje termodynamiczne (
) opisują właściwości substancji w roztworze. Bardzo często interesują nas jednak nie same wartości cząstkowe molowych funkcji termodynamicznych, a jedynie ich zmiany w procesie tworzenia roztworu (mieszaniny) z czystych składników. Zmiany funkcji termodynamicznych w procesie mieszania noszą nazwę termodynamicznych funkcji mieszania, a oznaczać je będziemy przez Y^M. Z definicji:

gdzie:
jest wartścią funkcji termodynamicznej dla roztworu złożonego z n₁ moli rozpuszczalnika i n₂ moli substancji rozpuszczonej, zaś Y⁰ jest sumą właściwości termodynamicznej składników przed zmieszaniem:
w równaniu tym
i
są wartościami ekstensywnej funkcji termodynamicznej czystych składników. Termodynamiczne funkcje mieszania odnoszą zatem właściwości roztworów do właściwości czystych składników.

Bardzo interesujące jest odniesienie właściwości roztworów rzeczywistych do właściwości roztworów doskonałych (idealnych).

Właściwości roztworów rzeczywistych porównuje się z właściwościami roztworów doskonałych przez wprowadzenie termodynamicznych funkcji nadmiaru Y^E:

w tym równaniu
, zaś

2. Opracowanie wyników:

Gęstości roztworów wyznaczone metodą piknometryczną:

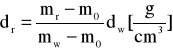
gdzie: d - gęstość roztworu [g/cm³]; m_r - masa piknometru wypełnionego roztworem [g]; m_w - masa piknometru wypełnionego wodą [g]; m₀ - masa pustego piknometru [g]; d_w - gęstość wody w temperaturze pomiaru [g/cm³]- w 20 °C wynosi 0,99821 g/cm³

Gęstość roztworów można obliczyć teoretyczne z następującej zależności:

gdzie: x_i = x_A

Lp.	Masa suchego piknometru [g]	Masa piknometru z wodą [g]	Masa piknometru z roztworem [g]	Skład mieszaniny od ułamka molowego alkoholu	Gęstość wyznaczona metodą piknometryczną [g/cm^3]	Gęstość teoretycznie [g/cm^3]	Błąd procentowy gęstości [%]
1	7,99912	12,32925	12,32925 (H2O)	0	0,99821	0,99100	0,73
2	6,27017	12,7107	12,20043	0,2	0,91912	0,92016	0,11
3	6,91007	10,8999	10,39902	0,4	0,87290	0,86728	0,65
4	6,7391	11,04926	10,33938	0,6	0,83381	0,83235	0,17
5	7,68948	11,64908	10,89916	0,8	0,80916	0,81539	0,76
6	7,99912	12,32925	11,39921 (propanol-1)	1	0,78381	0,81638	3,99

Z danych zawartych w tabeli wyznaczam wykres zależności gęstości roztworu od ułamka molowego alkoholu.

Objętości roztworów, masy substancji, liczby moli oraz objętości molowe roztworów w poszczególnych roztworach.

Objętości roztworów obliczyć można z następującej zależności:

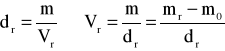
Masy substancji zawartych w roztworach obliczyć można z następujących zależności:

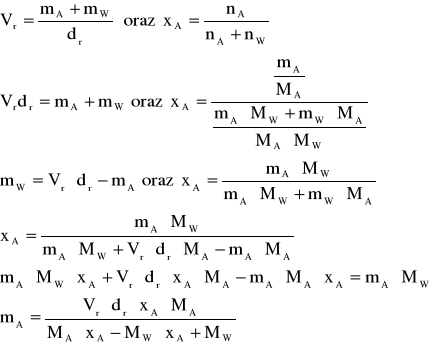
Liczbę moli oblicza się z zależności:

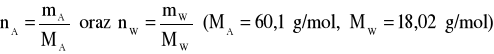
Objętości molowe roztworów wyznaczamy z zależności:

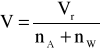
Lp.	Skład mieszaniny od ułamka molowego alkoholu	Gęstość dr [g/cm^3]	Masa roztworu (mr - m0) [g]	Objętość roztworu Vr [cm^3]	Masa alkoholu mA [g]	Masa wody mW [g]	Liczba moli alkoholu nA [mol]	Liczba moli wody nW [mol]	Objętość molowa roztworu V [cm^3/mol]
1	0	0,99821 (H2O)	4,33013	4,33789	0,00000	4,33013	0,00000	0,24030	18,05231
2	0,2	0,91912	5,93026	6,45208	2,69639	3,23387	0,04487	0,17946	28,76217
3	0,4	0,87290	3,48895	3,99698	2,40659	1,08236	0,04004	0,06006	39,92689
4	0,6	0,83381	3,60028	4,31789	3,00051	0,59977	0,04993	0,03328	51,89219
5	0,8	0,80916	3,20968	3,96670	2,98586	0,22382	0,04968	0,01242	63,87395
6	1	0,78381 (propanol-1)	3,40009	4,33789	3,40009	0,00000	0,05657	0,00000	76,67664

Z danych zawartych w tabeli wyznaczam wykres zależności objętości molowej roztworu od ułamka molowego alkoholu.

Objętości cząstkowe molowe i objętości nadmiarowe roztworów.

Objętości cząstkowe molowe
dla roztworów wyznaczam metodą graficzną z wykorzystaniem wykresu zależności objętości molowych roztworów od ułamka molowego. Metoda graficzna polega na przeprowadzeniu stycznych do krzywej w punktach wyznaczonych przez skład roztworów (zależne od ułamka molowego alkoholu).

Objętości nadmiarowe wyznaczone z zależności:

gdzie: V - objętość molowa roztworów;
- objętości cząstkowe czystych substancji w odpowiednim roztworze; x_i - ułamek molowy substancji w roztworach.

Objętości nadmiarowe mogą być również teoretycznie wyznaczone z zależności:

gdzie: A₀ = -5,8380; A₁ = -15,2786; A₂ = -22,4778; A₃ = -10,8; x₁ = x_A; x₂ = x_W.

Lp.	Skład mieszaniny od ułamka molowego alkoholu	Objętość molowa cząstkowa alkoholu wyznaczona z wykresu objętości molowej	Objętość molowa cząstkowa wody wyznaczona z wykresu objętości molowej	Objętość molowa roztworu [cm3/mol]	Objętość nadmiarowa wyznaczona [cm3/mol]	Objętość nadmiarowa teoretyczna [cm3/mol]	Błąd procentowy objętości nadmiarowej [%]
1	0	76,37017	18,05231	18,05231	0	0	0
2	0,2	76,42234	17,55766	28,76217	-0,56842	-0,5751987	1,18
3	0,4	76,47404	16,60601	39,92689	-0,62634	-0,6316339	0,84
4	0,6	76,56511	16,35596	51,89219	-0,58926	-0,5832115	1,04
5	0,8	76,60345	14,89362	63,87395	-0,38753	-0,3954099	1,99
6	1	76,67664	12,2186	76,67664	0	0	0

Z danych zawartych w tabeli wyznaczam wykres zależności objętości nadmiarowej roztworu od ułamka molowego alkoholu.

Błąd procentowy gęstości propanolu-1:

Gęstość propanolu-1 (wyznaczona)	Gęstość propanolu-1 (tablicowa)	Błąd procentowy
0,78381	0,7995	1,96 %

3. Wnioski:

Przebieg zależności cząstkowych objętości molowych od składu w układzie podwójnym woda - propanol-1 jest typowy. Cząstkowa objętość molowa wody i propanolu-1 nie ulega znacznym zmianom. Objętości nadmiarowe przyjmują wartości ujemne z czego wynika, iż objętość roztworów podczas mieszania zmniejsza się.

4. Literatura:

Kazimierz Gumiński „Wykłady z chemii fizycznej”.

Lucjan Sobczyk, Adolf Kisza, Kazimierz Gatner, Aleksander Koll „Eksperymentalna chemia fizyczna”

Witold Mizerski „Tablice chemiczne”.

4

---