Ćwiczenie: Siatki azymutalne w położeniu biegunowym

Przed przystąpieniem do wykonania ćwiczenia należy zapoznać się z omówieniem siatek azymutalnych w podręczniku Wprowadzenie do kartografii i topografii (podrozdział 4.3, s. 105-121).

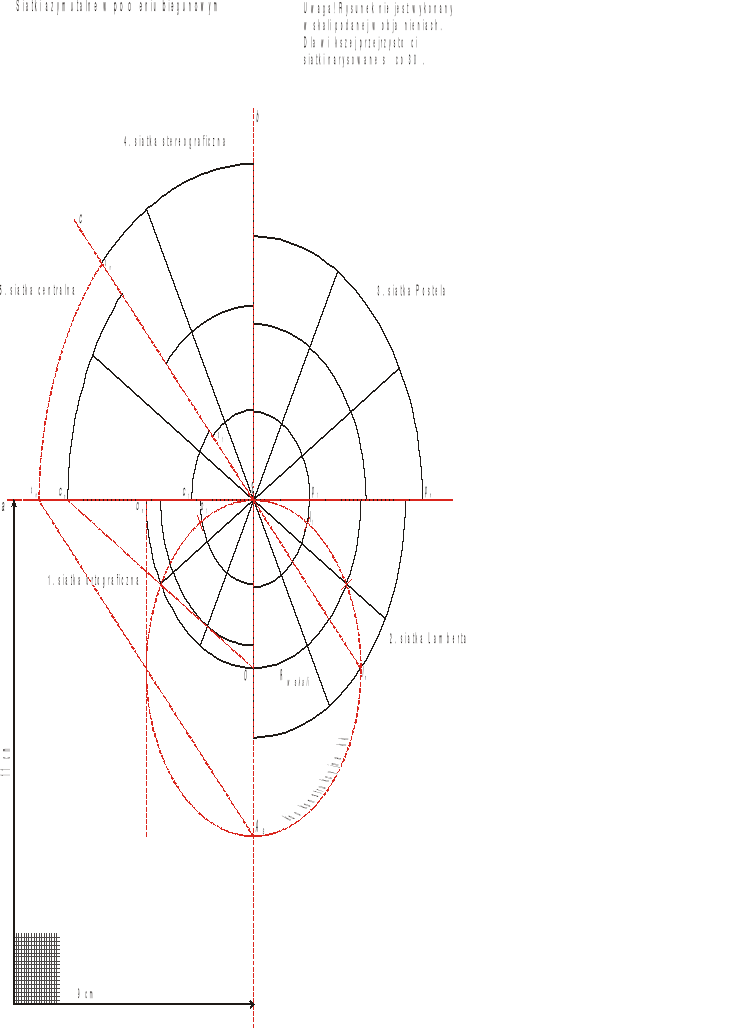
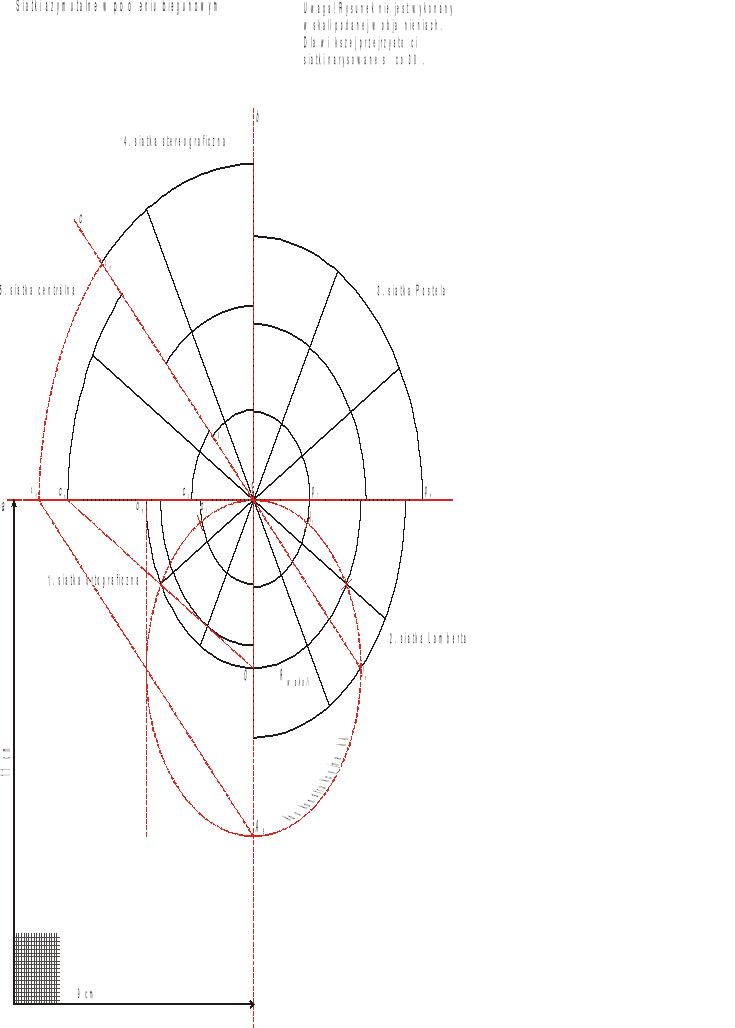
Siatki azymutalne powstają w wyniku przeniesienia siatki geograficznej z kuli ziemskiej na płaszczyznę. Celem ćwiczenia jest nabycie umiejętności konstrukcji pięciu najpopularniejszych siatek azymutalnych (ortograficznej, Lamberta, Postela, stereograficznej i centralnej) w położeniu normalnym (biegunowym). Rysunek można wykonać w skali 1:150 000 000 (lub innej zaleconej przez prowadzącego ćwiczenia). Linie siatek powinny być rysowane co 10°.

Podstawowe przybory kreślarskie to: linijka, kątomierz, krzywiki, cyrkiel, ołówek HB, 2 rapidografy (cienki, np. 0,2 mm i grubszy, np. 0,5 mm).

Ćwiczenie realizowane jest w dwóch etapach:

I - narysowanie pięciu siatek azymutalnych w położeniu biegunowym

II - wrysowanie lądów w siatki.

Etap I rozpoczynamy od obliczenia długości promienia Ziemi R w skali np. 1:150 000 000

Uwaga! Wymagana dokładność graficzna wynosi 0,1 mm.

Na arkuszu papieru milimetrowego A4 w ułożeniu pionowym rysujemy ołówkiem poziomą linię a i prostopadłą do niej linię pionową b tak, aby punkt ich przecięcia wypadał zgodnie z podanymi wymiarami (na pełnym centymetrze). Linia a obrazuje płaszczyznę styczności, na którą nanoszone będą punkty wyznaczające położenie obrazów równoleżników w poszczególnych siatkach. Obliczonym promieniem R_{w skali} = 4,25 cm kreślimy zielonym tuszem koło konstrukcyjne kk, będące obrazem Ziemi, tak by było ono styczne do prostej a w punkcie jej przecięcia z b (punkt styczności S). Północną połowę tego koła dzielimy kątomierzem co 10°, zaczynając podział od linii pionowej b i oznaczając go jedynie na obwodzie kk.

1) Siatka ortograficzna

Punkty podziału ćwiartki NW koła konstrukcyjnego kk rzutujemy prostopadle na prostą a, otrzymując w ten sposób punkty wyznaczające długości promieni (o₁, o₂ ... o_n) obrazów poszczególnych równoleżników. Następnie z punktu S czarnym tuszem zakreślamy tymi promieniami łuki ćwiartek okręgów w części rysunku oznaczonej „1”. Dla uzyskania obrazu południków kąt prosty między liniami a i b w ćwiartce „1” dzielimy kątomierzem co 10° i rysujemy linie podziału z punktu S na zewnątrz, aż do skrajnego okręgu o_n. Uzyskujemy w ten sposób obraz ¼ półkuli w siatce ortograficznej.

2) Siatka Lamberta

Punkty podziału ćwiartki NE koła konstrukcyjnego kk łączymy cięciwami z punktem S, otrzymując w ten sposób długości promieni (l₁, l₂ ... l_n) obrazów poszczególnych równoleżników. Z punktu S zakreślamy tymi promieniami łuki ¼ okręgów między prostymi a i b w ćwiartce „2”. Obrazy południków rysujemy analogicznie jak w siatce ortograficznej (ćwiartka „1”). Uzyskany obraz odwzorowuje ¼ półkuli w siatce Lamberta.

3) Siatka Postela

Obliczamy długość ćwierci obwodu narysowanego już koła konstrukcyjnego kk:

Z punktu S obliczoną długością p_n zakreślamy ćwierć okręgu między liniami a i b w ćwiartce rysunku oznaczonej „3”. Jest to obraz równika. Promienie okręgów obrazujących pozostałe równoleżniki uzyskujemy z podziału największego promienia (6,67 cm) na dziewięć równych części (co 10°). Rysując południki analogicznie jak w siatce ortograficznej (ćwiartka „1”), uzyskujemy obraz ¼ półkuli w siatce Postela.

4) Siatka stereograficzna

Punkty podziału kk w ćwiartce NW rzutujemy na prostą a z punktu A_S (antypoda punktu S), otrzymując w ten sposób punkty wyznaczające długości promieni (s₁, s₂ ... s_n) obrazów poszczególnych równoleżników. Z punktu S wyprowadzamy półprostą Sc dzielącą NW ćwiartkę rysunku na dwie części „4” i „5”. W części „4” zakreślamy promieniami s₁, s₂ ... s_n łuki stanowiące ¹/₈ okręgów. Obrazy południków rysujemy analogicznie jak siatce ortograficznej (punkt 1). Uzyskany obraz przedstawia ¹/₈ półkuli w siatce stereograficznej.

5) Siatka centralna

Punkty podziału NW ćwiartki koła konstrukcyjnego kk rzutujemy na prostą a ze środka tego koła (punkt O), otrzymując w ten sposób punkty wyznaczające długości promieni (c₁, c₂ ... c_n) obrazów poszczególnych równoleżników. W siatce tej nie można zrzutować wszystkich punktów podziału kk. Z punktu S w części „5” (między prostą a i półprostą Sc) kreślimy promieniami c₁, c₂ ... c_n łuki stanowiące ¹/₈ okręgów. Obrazy południków rysujemy analogicznie jak w siatce ortograficznej (ćwiartka „1”). Uzyskany obraz przedstawia ¹/₈ części półkuli w siatce centralnej.

Etap II - wrysowanie lądów w siatki azymutalne biegunowe.

Korzystając z map atlasowych wykonanych w siatkach azymutalnych w położeniu biegunowym w zbliżonych skalach, np. 1:200 000 000 wrysowujemy lądy półkuli południowej lub północnej. Należy zwrócić szczególną uwagę na miejsca styku różnych siatek, które są liniami nieciągłości przebiegu linii brzegowej. Ważne jest zachowanie właściwego położenia wrysowywanych obszarów w układzie współrzędnych geograficznych.

Forma graficzna: Rysunek należy wykonać rapidografami czarnym tuszem, prowadząc cienkie linie siatki (np. o grubości 0,2 mm). Obrazy skrajnych równoleżników o_n l_n p_n s_n i c_n obwodzimy ramką o grubości 0,5 mm i wprowadzamy dla całości wspólny opis południków i równoleżników. Elementy konstrukcyjne rysunku: kk i przykładowo wybrane linie rzutów rysujemy kolorowym tuszem, np. zielonym. Zarysy lądów wykonujemy czarnym tuszem grubością 0,1 mm, ich wnętrza zaś zamalowujemy kredką o jasnej pastelowej barwie.

*

Zestawienie siatek na jednym arkuszu umożliwia porównanie ich własności, zwłaszcza zniekształceń długości w kierunku południków i równoleżników oraz zniekształceń pól powierzchni. Doskonale w tym ćwiczeniu widoczne są różnice między skalą główną a skalą miejscową (lokalną). Ta pierwsza zachowana jest tylko w miejscach zerowych zniekształceń. Tam, gdzie następuje zniekształcenie długości, nie funkcjonuje skala główna i można mówić jedynie o skali miejscowej. Innymi słowy skala główna opisana na mapie uprawnia nas do pomiaru długości tylko wzdłuż linii, które nie ulegają zniekształceniu. Jeśli np. w siatce ortograficznej w położeniu biegunowym nie ma zniekształceń długości w kierunku równoleżników (zachowana jest tu skala główna), to dzięki zestawieniu od razu widać, że w pozostałych siatkach obrazy równoleżników są dłuższe (wzdłuż tych linii w każdej siatce występują indywidualne skale miejscowe i to większe od skali głównej). Jeśli w siatce Postela w położeniu normalnym południki odwzorowują się wiernie długościowo (skala główna), to łatwo zauważyć, że w siatce ortograficznej i Lamberta skale wzdłuż południków są mniejsze od skali głównej (linie te ulegają skróceniu w stosunku do oryginału), a w siatkach stereograficznej i centralnej skale wzdłuż południków są większe od skali głównej (obrazy południków są dłuższe od oryginałów). Ponadto w biegunowych siatkach azymutalnych skale miejscowe nie są stałe wzdłuż linii południków, tak jak ma to miejsce w przypadku równoleżników. Na rysunku łatwo zauważymy, że na liniach obrazujących dowolny równoleżnik, łuki 10-stopniowe mają zawsze w danej siatce jednakowe długości. Inaczej jest na obrazach południków, gdzie odcinki odpowiadające łukom 10-stopniowym mają długości zbliżone do oryginału (obraz w siatce Postela) tylko w pobliżu bieguna stycznego. Im dalej od miejsca zerowego zniekształcenia, tym odcinki odpowiadające łukom 10-stopniowym są bardziej skrócone lub wydłużone, co świadczy o rosnących zniekształceniach, a zatem zmieniających się skalach miejscowych.

---