14. Pomiary oscyloskopem

16.1 Oscyloskop analogowy

Oscyloskop jest najbardziej uniwersalnym elektronicznym przyrządem pomiarowym, stosowanym do pomiarów i badań różnorodnych okresowych i nieokresowych przebiegów elektrycznych, a przy zastosowaniu odpowiednich przetworników, także wielkości nieelektrycznych.

Ze względu na budowę i sposób zobrazowania badanych sygnałów oscyloskopy dzielimy na analogowe (klasyczne) oraz cyfrowe. Uproszczony schemat blokowy oscyloskopu analogowego przedstawiono na rys. 16.1

Rys 16.1 Schemat blokowy oscyloskopu analogowego[2].

Badany sygnał jest doprowadzony do płytek Y lampy poprzez dzielnik napięcia DN_Y i wzmacniacz pomiarowy W_Y. Wzmacniacz ten ma regulowany i kalibrowany współczynnik wzmocnienia, co umożliwia określenie amplitudy sygnału badanego na podstawie pomiaru amplitudy sygnału obserwowanego na ekranie oscyloskopu.

W celu obserwacji przebiegów w funkcji czasu (przeł. P w pozycji 1) do płytek odchylania poziomego X musi być doprowadzone napięcie narastające liniowo w czasie wytwarzane w generatorze podstawy czasu GNP.

Aby obraz na ekranie oscyloskopu był stabilny, moment wyzwalania napięcia piłokształtnego w generatorze GNP musi być synchronizowany za pomocą sygnału badanego lub też z zewnętrznego źródła synchronizacji.

W przypadku konieczności obserwacji wzajemnej zależności dwóch sygnałów (przeł. P w pozycji 2) drugi sygnał doprowadza się do płytek X poprzez dzielnik napięcia DN_X oraz wzmacniacz W_X. Blok UF jest układem formującym ujemne impulsy doprowadzane do siatki lampy, w celu wygaszenia plamki świetlnej w czasie powrotu.

Oscyloskop jest zasilany z dwóch zasilaczy napięcia stałego; Z₁ - wysokonapięciowego zasilającego siatkę i anody lampy przez dzielnik DN; Z₂ - niskonapięciowego zasilającego pozostałe układy.

Oprócz wymienionych układów oscyloskop może być wyposażony w wiele innych, takich jak: linia opóźniająca, kalibrator napięcia KN, kalibrator osi czasu, układ lokalizacji strumienia oraz przełączniki dające możliwość obserwacji kilku przebiegów jednocześnie.

Zasadniczym elementem oscyloskopu jest lampa oscyloskopowa, w której strumień elektronów, padając na ekran pokryty luminoforem, powoduje jego świecenie. Schemat rozmieszczenia elektrod w lampie przedstawia rys. 16.2

Rys 16.2 Schemat lampy oscyloskopowej[2].

Efekt zmiany jasności obrazu uzyskuje się poprzez regulację potencjału siatki S1, która steruje ilością elektronów przepuszczanych w kierunku ekranu. Zespół anod A1 A2 tworzy soczewkę elektrostatyczną, której zadaniem jest odpowiednie skupienie oraz przyspieszenie strumienia elektronów.

Jedną z cech lampy jest jej czułość. Jest ona definiowana następująco:

(16.1)

gdzie: h,a,l,d - oznaczenia zgodnie z rys 16.3,

Ua - napięcie ostatniej z anod przyspieszających

Rys 16.3 Zasada odchylania plamki za pomocą oscyloskopu[2].

Czułość współcześnie stosowanych lamp wynosi 0,1 ÷ 1 mm/V.

Generator podstawy czasu.

Obserwacja napięcia zmiennego na ekranie lampy oscyloskopowej wymaga jednoczesnego oddziaływania na strumień elektronów dwu sił. Odchylenie plamki w kierunku pionowym jest proporcjonalne do przyłożonego napięcia mierzonego, a odchylenie plamki w kierunku poziomym musi być wprost proporcjonalne do czasu, co uzyskuje się przez przyłożenie do płytek X napięcia narastającego liniowo w funkcji czasu. Ponieważ ekran ma skończone wymiary, przeto plamka po dojściu do prawego skraju pola pomiarowego musi powrócić z powrotem, a napięcie odchylające powinno zmaleć do swej wartości początkowej. Wytworzony w ten sposób sygnał nosi nazwę piłokształtnego a linia pozioma przez niego rysowana nazywa się liniową podstawą czasu.

Zasada powstawania obrazu na ekranie pokazana jest na rys 16.4

Rys 16.4 Zasada powstawania obrazu na ekranie lampy oscyloskopowej.

Obraz powrotny jest dla obserwacji przebiegu niepotrzebny i dlatego w czasie jego trwania do siatki pierwszej lampy oscyloskopowej doprowadza się ujemny impuls wygaszający strumień. Aby obraz na ekranie był obserwowany, powinien on pojawiać się wielokrotnie, a napięcie piłokształtne musi powtarzać się zgodnie z doprowadzonym sygnałem. Zgodność wzajemnego położenia napięcia podstawy czasu i sygnału jest warunkiem koniecznym do nałożenia się na siebie kolejnych obrazów, nieruchomego więc powstania nieruchomego obrazu na ekranie. Tę zgodność zapewniają w oscyloskopie układy synchronizacji i wyzwalania.

Liniowe narastanie napięcia uzyskuje się w układzie ładowania kondensatora prądem o stałej wartości przez dużą rezystancję i następnie rozładowywania przez małą rezystancję. Zasadę tę ilustruje rys 16.5

Rys 16.5 Zasada powstawania napięcia piłokształtnego.

Jednym z istotniejszych układów oscyloskopu decydujących o jego jakości, czyli również o obszarach zastosowań jest wzmacniacz odchylania pionowego. Podstawowe jego parametry to: czułość, częstotliwość graniczna, impedancja wejściowa i maksymalne napięcie wejściowe. Schemat blokowy wzmacniacza przedstawiony jest na rys16.6

Rys 16.6 Schemat blokowy wzmacniacza odchylenia pionowego.

Zadaniem tłumika jest zmniejszenie sygnału wejściowego do wartości zależnej od czułości wzmacniacza i wymaganej amplitudy obrazu na ekranie. Wzmacniacz wyposażony jest w regulator wzmocnienia oraz układ przesuwania pionowego. Ponadto w wielu oscyloskopach stosuje się linię opóźniającą dającą możliwość wystartowania generatora podstawy czasu, zanim pojawi się sygnał badany. Pasmo przenoszenia wzmacniacza Y definiuje się jako częstotliwość, przy której czułość oscyloskopu maleje o 3dB, to znaczy do wartości 0,707 czułości początkowej. Obecnie produkowane oscyloskopy charakteryzują się pasmem przenoszenia do 400MHz.

16.2 Oscyloskop cyfrowy

Zasada pracy oscyloskopu cyfrowego polega na próbkowaniu analogowego sygnału badanego za pomocą przetwornika A/C. Przetworzone na sygnały cyfrowe wartości chwilowe przebiegu badanego są wprowadzane do pamięci cyfrowej, w której mogą być przechowywane dowolnie długo. Odwzorowanie przebiegu polega na przetworzeniu w odpowiedniej kolejności zawartości pamięci na sygnały analogowe i doprowadzenie tych sygnałów do elektrod odchylania pionowego lampy oscyloskopowej. Na podstawie zawartości pamięci cyfrowej, mikroprocesor wchodzący w skład oscyloskopu oblicza wybrane miary sygnału badanego, a wyniki obliczeń wskazuje wskaźnik cyfrowy. Mogą to być takie miary jak wartość średnia, maksymalna, skuteczna, czas narastania lub opadania impulsu, składowa stała itp. Niektóre oscyloskopy umożliwiają również analizę widmową przebiegu badanego. Odwzorowanie i analiza przebiegu badanego na podstawie próbek wymaga, aby częstotliwość próbkowania była co najmniej dwukrotnie większa od górnej częstotliwości granicznej tego przebiegu. Pomiarów napięć oraz pomiarów w dziedzinie czasu dokonuje się za pomocą kursorów pionowych i poziomych lub sprzężonych(przesuwanych po badanym przebiegu), a wyniki wyświetla się na ekranie w postaci znaków alfanumerycznych. Oscyloskop cyfrowy umożliwia uśrednianie przebiegów, polegające na obliczaniu wartości średniej przebiegu z pewnej liczby okresów i zobrazowaniu wyniku na ekranie. Uśrednianie powoduje zwiększenie stosunku sygnału użytecznego do szumu. Ponadto oscyloskopy cyfrowe umożliwiają ciągłe śledzenie przebiegu ( pamięć pracuje jako rejestr przesuwny) i zapamiętanie tylko interesującego fragmentu przebiegu. Istnieje również możliwość wykonywania operacji arytmetycznych na zbiorach danych, możliwość współpracy z drukarką oraz praca w systemie pomiarowym.

W nowoczesnych oscyloskopach cyfrowych do wizualizacji przebiegów, stosuje się lampy kineskopowe (monochromatyczne lub kolorowe) lub ekrany ciekłokrystaliczne.

Obecnie produkowane oscyloskopy cyfrowe charakteryzują się pasmem przenoszenia do 20GHz oraz szybkości próbkowania 2GS/s/Ch (109 próbek na sekundę na kanał). Oscyloskopy cyfrowe są wyposażone w interfejs GPIB (IEEE 488, IEC 625) lub RS 232 umożliwiające pracę w systemie pomiarowym.

Rys 16.7 Schemat blokowy oscyloskopu cyfrowego[2].

16.3 Zastosowanie oscyloskopu w technice pomiarowej

Charakterystyki Prądowo-Napięciowe

Jak już wspomniano wcześniej, oscyloskop elektroniczny umożliwia obserwację przebiegów wielkości elektrycznych w czasie, badania kształtu tych przebiegów oraz rejestrację odwzorowań zależności funkcyjnych miedzy wielkościami. Za pomocą oscyloskopu można zmierzyć m.in. napięcie, częstotliwość, przesunięcie fazowe oraz stosując odpowiednie przetworniki, różnorodne wielkości fizyczne dające się przetworzyć na wielkość elektryczną.

Najszybszą metodą pomiaru statycznej charakterystyki prądowo- napięciowej diod i tranzystorów jest dokonanie tego za pomocą oscyloskopu. Do płytek X należy doprowadzić sygnał proporcjonalny do napięcia, natomiast do płytek Y do prądu.

Układ do wyznaczania charakterystyk diod D₁ - D_n przedstawia rys. 16.8

Rys 16.8 Układ po wyznaczania charakterystyk statycznych
prądowo- napięciowych diod.

W zależności od położenia przełącznika P włączającego diody prostownicze D_p1 i D_p2 na ekranie uzyskuje się odpowiednio:

1. pełną charakterystykę w kierunku przewodzenia i zaporowym,

2. charakterystykę w kierunku zaporowym,

3. charakterystykę w kierunku przewodzenia.

Układ do wizualizacji rodziny charakterystyk wyjściowych tranzystora bipolarnego I_C = f(U_CE) przy I_B = const. przedstawia rys 16.9

Rys 16.9 Schemat układu do wyznaczania rodziny
charakterystyk wyjściowych tranzystora w układzie OE.

W układzie tym dokonywana jest cykliczna zmiana wartości prądu bazy I_B. Zmiana następuje z chwila przejścia przez zero przemiennego napięcia zasilającego układ pomiarowy.

Pomiar Rezystancji

Oscyloskop o znanej rezystancji wejściowej R_WE może być zastosowany do pomiaru dużych wartości rezystancji. Układ połączeń przedstawiony jest na rys 16.10

Rys 16.10 Schemat układu do pomiaru rezystancji.

Z ekranu oscyloskopu odczytuje się wartości napięć w przypadku bezpośredniego dołączenia generatora pomiarowego do zacisków wejściowych (U₁) i dołączenia generatora poprzez rezystor mierzony (U₂). Rezystancję R_X wyznacza się z równania

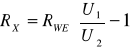
(16.2)

Pomiar Pojemności

Pomiaru pojemności kondensatorów z zastosowaniem oscyloskopu można dokonać w układzie przedstawionym na rys. 16.11

Rys 16.11 Schemat układu do pomiaru pojemności kondensatorów.

Można dowieść, że jeśli stała czasowa układu R_S⋅C_X jest co najmniej pięciokrotnie większa od okresu sygnału prostokątnego generatora pomiarowego o współczynniku wypełnienia 0,5, to wartość międzyszczytowa napięcia na kondensatorze zmienia się w przybliżeniu odwrotnie proporcjonalnie do wartości pojemności.

Jeżeli więc spełniony zostanie warunek

oraz C_X > C_WE

wartość pojemności C_X można wyznaczyć z zależności

(16.3)

gdzie: U₃ - wartość międzyszczytowa napięcia fali prostokątnej miedzy punktami
1-1przed dołączeniem C_X,

U₄ - wartość międzyszczytowa napięcia piłokształtnego między punktami
1-1 po dołączeniu C_X,

T - okres napięcia prostokątnego,

R =

Oscyloskop elektroniczny pozwala także dokonać pomiaru indukcyjności i wybranych parametrów materiałów magnetycznych w szerokim zakresie częstotliwości i natężenia pola magnetycznego.

Pomiar Przesunięcia Fazowego

Do podstawowych metod pomiaru przesunięcia fazowego między dwoma sygnałami o tej samej częstotliwości należą:

• metoda przekształcenia w przedział czasowy,

• metoda kompensacyjna,

• metoda elipsy.

Metoda przekształcenia w przedział czasowy polega na wykryciu chwil osiągnięcia przez dwa sygnały określonej wartości, np. zera.

W przypadku zastosowania oscyloskopu dwukanałowego, postępowanie sprowadza się do pomiaru odległości pomiędzy punktami przecięcia osi czasu przez badane przebiegi.

Rys 16.12 Pomiar przesunięcia fazowego metodą
przekształcenia w przedział czasowy.

Kąt przesunięcia fazowego oblicza się ze wzoru

(16.4)

gdzie:
- odstęp między punktami przecięcia osi czasu przez oba sygnały,

X - długość odcinka odpowiadającego okresowi badanego sygnału.

Pomiar przesunięcia fazowego metodą kompensacyjną polega na kompensacji występującej różnicy faz do zera lub dopełnienie do 2π za pomocą kalibrowanego przesuwnika fazowego w układzie jak na rys.16.13

Rys 16.13 Schemat układu do pomiaru przesunięcia fazowego,

metodą kompensacyjną.

Metoda elipsy polega na pomiarze parametrów elipsy powstającej na ekranie oscyloskopu jednokanałowego. Gdy na obie pary płytek odchylających zostaną przyłożone napięcia o tej samej częstotliwości, lecz przesunięte w fazie.

Napięcie przyłożone do płytek X powoduje odchylenie strumienia elektronów w kierunku osi poziomej

(16.5)

analogicznie w kierunku osi pionowej

(16.6)

gdzie: K_X i K_Y czułości toru X i Y [V/mm].

Wyrażenia powyższe są parametrycznymi równaniami elipsy, którą kreśli promień elektronów w czasie równym okresowi napięć odchylających. Dla przypadku przecinania osi pionowej w momencie t₁ = 0, otrzymuje się

(16.7)

i odpowiednio odchylenie pionowe wynosi

(16.8)

Maksymalne odchylenie pionowe

Możemy więc wyznaczyć

(16.9)

Analogicznie można napisać dla odchylenia w kierunku osi poziomej

(16.10)

Rys 16.14 Pomiar przesunięcia fazowego metodą elipsy
a) dla kątów dużych, b) dla kątów małych.

Opisana metodę stosuje się do pomiaru katów ϕ > π/3.

Dla kątów małych dokładniejsze wyniki uzyskuje się przez wyznaczenie przesunięcia fazowego z ilorazu obu półosi elipsy, tzn.

(16.11)

Wyznaczenie przesunięcia fazowego za pomocą oscyloskopu umożliwia wyznaczenie transmitancji czwórników liniowych. Wyraża się ona następująco:

K(ω)=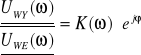
(16.12)

gdzie:
-tłumienie czwórnika.

Pomiar Częstotliwości

Pomiaru częstotliwości za pomocą oscyloskopu dokonuje się najczęściej dwoma metodami:

• przez porównanie z częstotliwością podstawy czasu,

• metodą krzywych interferencyjnych zwanych też Lissajous`a.

Porównanie z częstotliwością podstawy czasu polega na określeniu, z nastaw przełączników generatora podstawy czasu oscyloskopu czasu T, odpowiadającego jednemu okresowi badanego przebiegu. Mierzona częstotliwość wynosi

f=

Znacznie dokładniejsze wyniki daje metoda porównania częstotliwości badanego przebiegu z częstotliwością generatora wzorcowego przy zastosowaniu oscyloskopu jako detektora błędu. Do jednej pary płytek odchylających doprowadza się napięcie o częstotliwości badanej fy, a do drugiej pary płytek napięcie z generatora wzorcowego o regulowanej w sposób ciągły częstotliwości fx.

Rys 16.15 Układ do pomiaru częstotliwości
a) sposób obliczenia stosunku dwóch częstotliwości b).

Przez jednoczesne wysterowanie toru X i Y dwoma różnymi sygnałami na ekranie powstają figury Lissajous. Jeżeli obu częstotliwości jest równy liczbie całkowitej lub stosunkowi dwóch liczb całkowitych, wtedy na ekranie otrzymuje się obraz nieruchomy.

Częstotliwość mierzoną wyznacza się prowadząc dwie wzajemnie prostopadłe sieczne przecinające jak na rys.16.15 powstającą figurę i określając liczby punktów przecięcia; ich stosunek wskazuje ile razy częstotliwość badana jest większa lub mniejsza od częstotliwości wzorcowej.

Dla takiego samego stosunku częstotliwości uzyskuje się różne obrazy na ekranie oscyloskopu w zależności od różnicy faz pomiędzy obu sygnałami.

Rys 16.16 Przykłady figur Lissajous.

Pomiar Mocy

Moc za pomocą oscyloskopu można mierzyć w układzie przedstawionym poniżej.

Rys 16.17 Schemat układu do pomiaru mocy.

Odchylenie pionowe y jest proporcjonalne do spadku napięcia na impedancji obciążenia

(16.13)

Odchylenie poziome x jest proporcjonalne do wartości prądu płynącego przez obciążenie

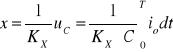
(16.14)

Powierzchnia S elipsy, zakreślonej przez plamkę na ekranie w ciągu jednego okresu T badanego przebiegu, jest określona zależnością

(16.15)

Moc czynną obciążenia można wyznaczyć ze wzoru

P_O=K∙S∙C∙f (16.16)

gdzie: K = K_X ∙K_Y oraz f = 1/T.

Prostszym sposobem pomiaru mocy czynnej z zastosowaniem oscyloskopu jest układ przedstawiony na rys 16.18

Rys 16.18 Schemat układu do pomiaru mocy.

Moc pozorną badanego obciążenia oblicza się następująco

(16.17)

gdzie: X,Y - wartości międzyszczytowe obrazu w kierunku x i y,

R - rezystancja szeregowa,

K_X, K_Y - torów x i y.

Moc czynna dla rozpatrywanego układu jest równa

(16.18)

Pomiar Współczynników Charakteryzujących Parametry Modulacji

Za pomocą oscyloskopu można również mierzyć współczynniki charakteryzujące parametry modulacji. W przypadku modulacji amplitudy głębokość modulacji określa się jako stosunek przyrostu amplitudy sygnału zmodulowanego wielkiej częstotliwości (w.cz.) do amplitudy sygnału fali nośnej.

(16.19)

gdzie: U_max i U_min oznaczają odpowiednio maksymalną oraz minimalną wartość napięcia sygnału zmodulowanego.

Schemat blokowy modulatora AM oraz obrazy przebiegów uzyskiwane na ekranie oscyloskopu z zaznaczonymi wartościami, z których można wyznaczyć głębokość modulacji przedstawia rys 16.19

Rys 16.19 a)Układ po pomiaru głębokości modulacji AM
b) obraz przebiegu przy wyzwalaniu sygnałem modulującym,
c) obraz przebiegu przy wyzwalaniu sygnałem fali nośnej,
d) obraz przebiegu przy metodzie X-Y.

Liniowość modulacji, która obok głębokości jest drugim bardzo ważnym parametrem sygnału zmodulowanego, można oszacować stosunkowo łatwo na podstawie obrazu uzyskanego przy metodzie trapezowej (rys.16.19 d.).

W przypadku modulacji częstotliwości FM częstotliwość chwilowa sygnału zmodulowanego częstotliwościowo wyraża się zależnością:

f(t) = f_O+ku(t) (16.20)

gdzie: u(t) jest napięciem modulującym.

Jeżeli napięcie modulacyjne jest sygnałem harmonicznym o częstotliwości f, to wzór powyższy można przekształcić do postaci

f(t) = f_O +
(16.21)

gdzie:
- dewiacja częstotliwości.

Stosunek dewiacji
i częstotliwości modulującej nosi nazwę indeksu modulacji β.

(16.22)

Rys 16.20 Układ do pomiaru dewiacji częstotliwości oraz indeksu modulacji.

Dewiację częstotliwości można określić na podstawie parametrów przebiegu z rys16 20b. wg wzoru

(16.23)

gdzie fo - częstotliwość odpowiadająca zerowemu napięciu modulującemu.

YY

x

GENERATOR

0

Y

X

YY

x

GENERATOR

0

Y

X

---