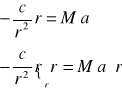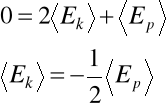4.3. Energia grawitacyjna jednorodnej kuli.

Aby obliczyć energię własną kuli o promieniu R i gęstości ρ obliczamy energię oddziaływania pomiędzy pełną kulą o promieniu r a otaczającą ja powłoką kulistą o grubości dr i masie dm. Budowanie kuli będzie polegać na doklejaniu kolejnych zewnętrznych powłok dopóki promień kuli nie osiągnie wartości R. Praca potrzebna na „doklejenie” powłoki - przeniesienie jej z ∞:

masa tak tworzonej kuli i powłoki jest równa odpowiednio:

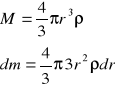
Całkowita praca potrzebna do utworzenia kuli:

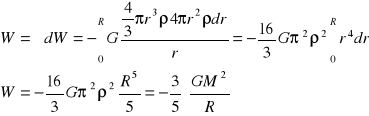
W ten sposób obliczamy energię grawitacyjną gwiazd i planet.

Przykładowo, grawitacyjna energia własna Słońca:

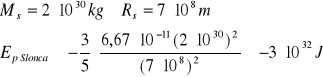
Jest to bardzo duża ilość energii i jest oczywiste, że w procesie grawitacyjnego zapadania się gwiazdy (do stadium białego karła o promieniu ok. 0,1 obecnego promienia Słońca) wyzwoli się ogromna ilość energii.

4.4. Prawa Keplera.

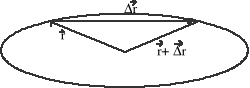
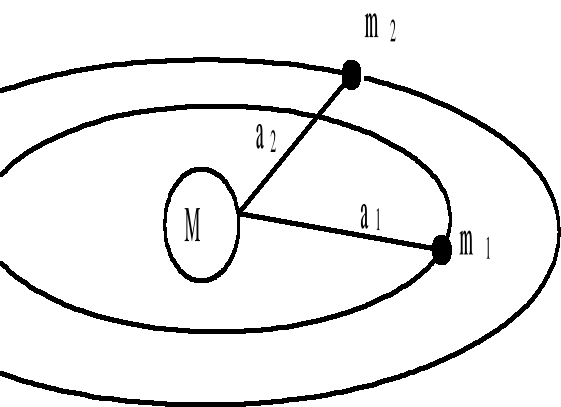
I Wszystkie planety krążą po elipsach. W ognisku elipsy znajduje się Słońce.

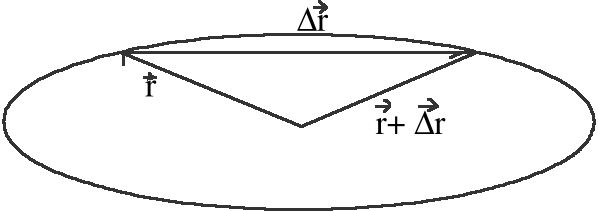
II Pola zakreślane przez wektor wodzący (od Słońca) w jednakowych odstępach czasu są równe.

Zakreślane pole:

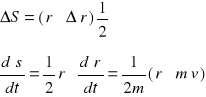
tzw. „prędkość polowa”

jeżeli nie działają siły zewnętrzne:

.

III Kwadraty okresów obiegów różnych planet dookoła słońca są proporcjonalne do sześcianów dużych półosi elipsy.

Powodem ruchu po orbicie jest siła dośrodkowa - jest nią siła grawitacji:

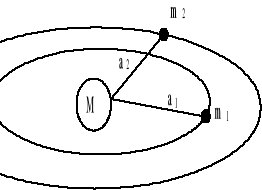
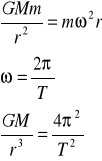
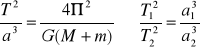
4.5. Przyspieszenie ziemskie.

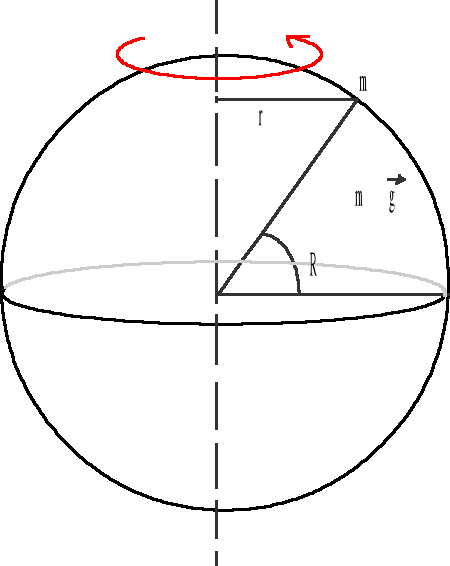
Energia potencjalna ciała o masie m znajdującego się w odległości x od powierzchni Ziemi jest:

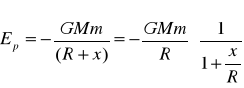
Zakładając że
możemy wyrażenie w nawiasie rozwinąć w szereg:

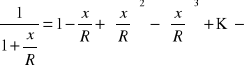
na podstawie założenia widać, że już trzeci wyraz szeregu jest zaniedbywalnie mały, a więc:

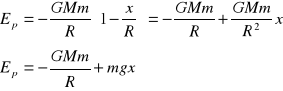
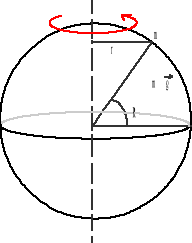
Wpływ szerokości geograficznej na wartość przyspieszenia ziemskiego.

W związku z ruchem obrotowym Ziemi, należy uwzględnić działanie siły odśrodkowej bezwładności. Ciężar ciała na szerokości geograficznej ϕ:

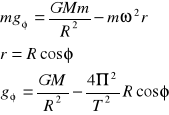
Na biegunie:

Na równiku

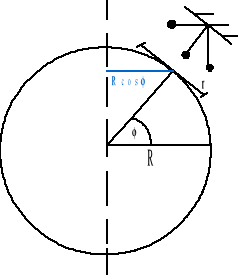
Wahadło Foucaulta

Kula wahadła Foucaulta wykonuje wahania nad pierścieniem o promieniu r, a płaszczyzna wahań obraca się w kierunku ruchu wskazówek zegara. Ziemia w swoim ruchu obrotowym stanowi nie inercjalny układ odniesienia, prędkości względne krańcowych punktów pierścienia - północnego i południowego są różne. Szybciej porusza się punkt leżący dalej od osi obrotu. Obliczamy prędkości liniowe odpowiednio północnego i południowego punktu pierścienia:

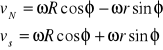
Różnica pomiędzy każdą z tych prędkości a prędkością środka pierścienia wahadła Foucaulta:

.

Skoro obwód pierścienia wynosi
więc pełny obrót płaszczyzny wahań jest:

Stąd okres obiegu:

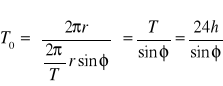
Na biegunie, gdy

Obserwacja wahadła Foucaulta stanowi dowód na nieinercjalność Ziemi.

4.6. Twierdzenie o wiriale w zastosowaniu do pola grawitacyjnego.

⇒
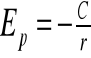
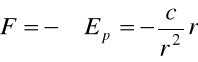
gdzie stała c=GMm

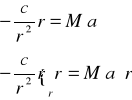
mnożąc obustronnie przez

czyli

wynika stąd, że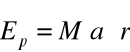

jeśli policzymy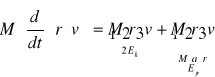
czyli: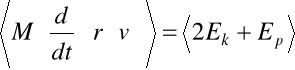

(*)

skoro

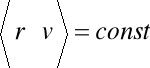
ponieważ gdy rośnie
to maleje
(prędkość orbitalna satelity). Cząstka będąca w polu siły proporcjonalnej do
jest cząstką w stanie związanym potencjałem przyciągającym.

Wówczas lewa strona równania (*) jest równa zero. A więc:

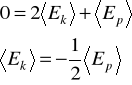
Stabilny układ grawitacyjny ma E_p , musi więc mieć (zgodnie z powyższymi równaniami) energię kinetyczną (E_k) - czyli jest w ruchu.

Na przykład zapadająca się gwiazda zwiększa
, więc rośnie jej energia kinetyczna, która przejawia się wzrostem temperatury!

Temperatura Słońca

Jak wyliczono wcześniej: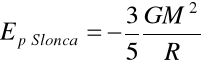

Z termodynamiki wiadomo, że średnia energia kinetyczna cząstki (He,H) jest:

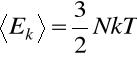
gdzie k - stała Boltzmana;

całkowita energia N-atomów: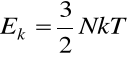

Z twierdzenia o wiriale otrzymano, że:

czyli:

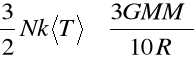
gdzie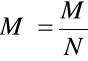
jest średnią masą atomu na Słońcu.

A zatem

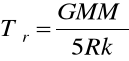
na Słońcu są zjonizowane atomy He i H czyli

a zatem podstawiając dane otrzymamy:

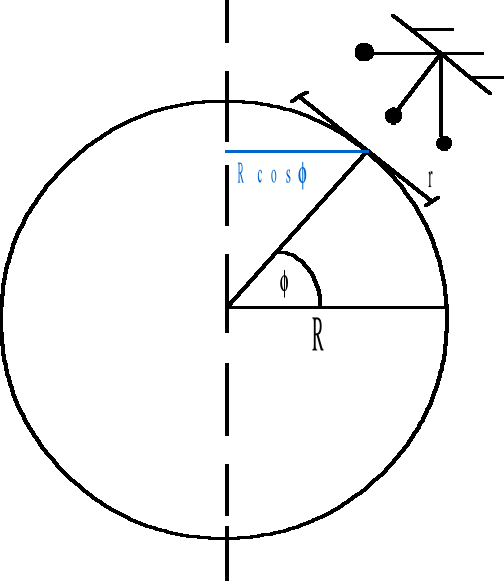
Na rys. brak wektorów sił, kąta fi