Numer ćwiczenia: 10 |
Temat ćwiczenia: Wyznaczanie stałej szybkości zmydlania estru z pomiarów przewodnictwa |
Data wykonania ćwiczenia: 14.01.2014r. |
|
|
Data oddania sprawozdania: 23.01.2014r. |
Grupa: A2 |
Góralik Monika |
Nazwisko sprawdzającego: dr Tomasz Uchacz |
Uwagi: |
Ocena: |
|
1. Cel ćwiczenia.
Celem ćwiczenia było wyznaczenie stałej szybkości reakcji zmydlenia octanu etylu wodorotlenkiem sodu na podstawie pomiarów konduktometrycznych w temperaturze pokojowej oraz wyższej.
2. Wykonanie.
Zmierzono konduktometrycznie przewodnictwo czystej wody destylowanej oraz 0,01 M roztworu chlorku potasu (by móc wyznaczyć stałą naczyńka)
Do kolby na 100 cm3 wprowadzono 0,4 cm3 octanu etylu, uzupełniono wodą do kreski oraz wymieszano
Zmierzono przewodnictwo roztworu sporządzonego z 25 cm3 0,05 M roztworu NaOH i 20 cm3 wody
Zmieszano ze sobą 25 cm3 0,05 M NaOH i 20 cm3 roztworu estru i mierzono przewodnictwo mieszaniny przez 20 minut (co minutę)
W łaźni wodnej o temperaturze 37,1 °C podgrzano, a następnie zmierzono przewodnictwo 0,05 M roztworu KCl, mieszaniny 25 cm3 0,05 M roztworu NaOH i 20 cm3 wody
Do podgrzanego w łaźni wodnej do wspomnianej wcześniej temperatury roztworu 20 cm3 estru dodano 25 cm3 0,05 M podgrzanego roztworu NaOH i dokonywano pomiaru przewodnictwa (co minutę przez 20 minut)
Podgrzano roztwór estru i NaOH do wrzenia, a następnie zmierzono przewodnictwo dwukrotnie: po ostygnięciu roztworu do 37,1 °C i po osiągnięciu temperatury pokojowej
(23,9 °C)
3. Wyniki.
Tabela1.: wyniki pomiarów przewodnictwa - roztwory octanu etylu z NaOH
t [s] |
23,9 °C |
37,1 °C |
||
|
L [S] |
k [S/cm] |
L [S] |
k [S/cm] |
0 |
0,00931 |
0,006937 |
0,00858 |
0,006393 |
60 |
0,00887 |
0,006609 |
0,00820 |
0,006110 |
120 |
0,00859 |
0,006400 |
0,00792 |
0,005901 |
180 |
0,00834 |
0,006214 |
0,00769 |
0,005730 |
240 |
0,00814 |
0,006065 |
0,00755 |
0,005625 |
300 |
0,00799 |
0,005953 |
0,00746 |
0,005558 |
360 |
0,00786 |
0,005856 |
0,00739 |
0,005506 |
420 |
0,00775 |
0,005774 |
0,00734 |
0,005469 |
480 |
0,00765 |
0,005700 |
0,00730 |
0,005439 |
540 |
0,00756 |
0,005633 |
0,00727 |
0,005417 |
600 |
0,00750 |
0,005588 |
0,00726 |
0,005409 |
660 |
0,00744 |
0,005543 |
0,00724 |
0,005394 |
720 |
0,00738 |
0,005499 |
0,00723 |
0,005387 |
780 |
0,00735 |
0,005476 |
0,00721 |
0,005372 |
840 |
0,00731 |
0,005446 |
0,00720 |
0,005364 |
900 |
0,00728 |
0,005424 |
0,00719 |
0,005357 |
960 |
0,00725 |
0,005402 |
0,00719 |
0,005357 |
1020 |
0,00723 |
0,005387 |
0,00717 |
0,005342 |
1080 |
0,00720 |
0,005364 |
0,00717 |
0,005342 |
1140 |
0,00719 |
0,005357 |
0,00717 |
0,005342 |
1200 |
0,00717 |
0,005342 |
0,00717 |
0,005342 |
∞ |
0,00752 |
0,005603 |
0,00730 |
0,005439 |
Tabela2.: wyniki pomiarów przewodnictwa - pozostałe roztwory
roztwór |
temperatura [°C] |
L [S] |
woda |
22,8 |
0,00000358 |
NaOH |
|
0,00827 |
KCl |
|
0,001824 |
KCl |
37,1 |
0,00177 |
NaOH+woda |
|
0,00750 |
4. Opracowanie wyników
- Stała naczynka pomiarowego - została obliczona na podstawie znajomości przewodnictwa 0,01 M KCl w temperaturze pokojowej oraz przewodnictwa właściwego:
gdzie:
k - stała naczynka do pomiaru
κKCl - przewodnictwo właściwe w temp. pokojowej (22,8 °C - ok. 296 K)
LKCl - zmierzone przewodnictwo roztworu KCl
κKCl=0,001359 S/cm
LKCl=0,001824 S
- Obliczono przewodnictwo właściwe badanych roztworów (κ0, κt, κ∞) ze wzoru:
gdzie:
κ - przewodnictwo właściwe [S/cm]
k - stała naczynka [1/cm]
L - przewodnictwo roztworu [S]
Wyniki umieszczono w tabeli 1.
- Na podstawie poniższych wzorów obliczono stężenia poszczególnych substancji:
gdzie:
a - początkowe stężenie NaOH
λNa+ i λOH- - przewodnictwa właściwe kationu sodu i anionu hydroksylowego
k0 - przewodnictwo właściwe mieszaniny NaOH i octanu etylu
gdzie:
kt - przewodnictwo właściwe mieszaniny po czasie t
x - stężenie anionu octanowego po czasie t
gdzie:
k∞ - przewodnictwo po zakończeniu reakcji zmydlania
b - początkowe stężenie octanu etylu
Δλ - λOH- - λCH3COO-
Wartości λNa+, λOH- i λCH3COO- w danych temperaturach obliczono na podstawie równoważnikowych przewodnictw jonowych. Wartości λ025°C oraz β zaczerpnięto z tabeli zamieszczonej w opisie ćwiczenia „Zależność przewodnictwa od stężenia”.
Wzór pozwalający na obliczenie λ0t dla danej temperatury:
λ0t= λ025°C[1+ β(t-25)]
Tabela3.: równoważnikowe przewodnictwa jonów
jon |
λ025°C [S*cm2/val] |
β |
λ023°C [S*cm2/val] |
λ037°C [S*cm2/val] |
Na+ |
50,1 |
0,0208 |
48,016 |
62,605 |
OH- |
198,3 |
0,0196 |
190,238 |
244,570 |
CH3COO- |
40,9 |
0,0206 |
39,215 |
51,010 |
- Obliczono stężenia jonu octanowego w roztworach po czasie t oraz obliczono stałą szybkości reakcji metodą rachunkową oraz graficzną. Stałą szybkości reakcji metodą rachunkową można obliczyć wzorem:
Tabela4.: stężenia jonu octanowego oraz stałe reakcji
t [s] |
23°C |
37°C |
||
|
x [mol/dm3] |
K [dm3/mol] |
x [mol/dm3] |
K [dm3/mol] |
60 |
0,00217 |
0,16823 |
0,00146 |
0,29275 |
120 |
0,00356 |
0,15816 |
0,00254 |
0,31200 |
180 |
0,00479 |
0,16474 |
0,00343 |
0,35226 |
240 |
0,00577 |
0,17251 |
0,00397 |
0,37319 |
300 |
0,00652 |
0,17837 |
0,00431 |
0,38778 |
360 |
0,00716 |
0,18919 |
0,00458 |
0,42047 |
420 |
0,00770 |
0,20530 |
0,00477 |
0,47841 |
480 |
0,00819 |
0,23569 |
0,00493 |
1,04609 |
540 |
0,00863 |
0,31564 |
0,00504 |
b/d |
600 |
0,00893 |
b/d |
0,00508 |
b/d |
660 |
0,00923 |
b/d |
0,00516 |
b/d |
720 |
0,00952 |
b/d |
0,00520 |
b/d |
780 |
0,00967 |
b/d |
0,00527 |
b/d |
840 |
0,00987 |
b/d |
0,00532 |
b/d |
900 |
0,01002 |
b/d |
0,00535 |
b/d |
960 |
0,01016 |
b/d |
0,00535 |
b/d |
1020 |
0,01026 |
b/d |
0,00543 |
b/d |
1080 |
0,01042 |
b/d |
0,00543 |
b/d |
1140 |
0,01046 |
b/d |
0,00543 |
b/d |
1200 |
0,01056 |
b/d |
0,00543 |
b/d |
Kśr* [dm3/mol*S] |
0,19864 |
0,45787 |
||
b/d - nie było możliwe obliczenie wartości logarytmu (
przyjęło wartość ujemną), a co za tym idzie - niemożliwe było wyznaczenie stałej)
* - obliczone dla dostępnych wartości
Metoda graficzna pozwala na wyznaczenie tych stałych poprzez narysowanie wykresu funkcji
=f(t). Wykresy wyznaczono tylko dla znanych wartości
. Współczynnik kierunkowy wykresu tej funkcji równa się K(a-b).
Wykres1.: funkcja
=f(t) - 23°C (296 K)
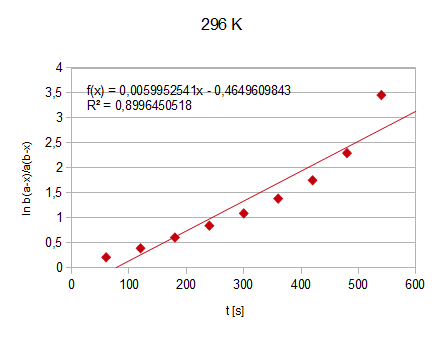
f(t)=0,005995x-0,464961
K=0,005995/(0,02912-0,00883)=0,29546 [dm3/mol*S]
Wykres2.: funkcja
=f(t) - 37°C (310 K) (pominięto jeden z punktów ze względu na zbyt dużą rozbieżność)
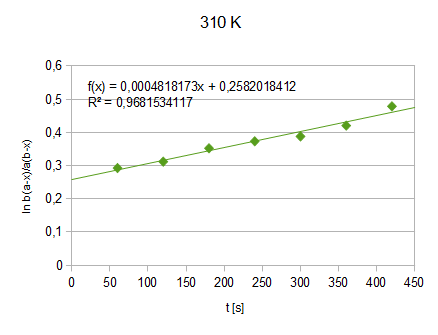
f(t)=0,000482x+0,258201
K=0,000482/(0,02081-0,00493)=0,03035 [dm3/mol*S]
- Energia aktywacji - możną ją obliczyć, opierając się na równaniu Arrheniusa:
Po scałkowaniu tego wyrażenia (zakładając, że energia aktywacji nie zależy od temperatury) można otrzymać:
Po przekształceniu można uzyskać wzór umożliwiający obliczenie pożądanej wartości:
Wartość energii aktywacji dla stałych wyznaczonych metodą rachunkową:
Wartość energii aktywacji dla stałych wyznaczonych metodą graficzną:
5. Wnioski.
Podczas ćwiczenia zauważono, że wraz z czasem przewodnictwo właściwe spada oraz że ten spadek jest coraz mniejszy, a pod koniec doświadczenia wręcz niezauważalny. Stałe reakcji wyznaczone metodą graficzną były zupełnie różne od tych wyznaczonych metodą rachunkową - mogło to być spowodowane nieliniowością zmiennych oraz ich niewielką ilością - obliczenie większości wartości nie było możliwe (patrz: uwaga pod tabelą 4). Z tych samych powodów obliczone energie aktywacji również drastycznie się różnią. Na błędne wyniki doświadczenia mogły wpłynąć zmiany temperatury podczas wykonywania eksperymentu (stała szybkości reakcji bardzo zależy od tego czynnika) oraz niedokładności w pomiarze czasu i niepewności pomiaru użytego do pomiarów potencjometru.
Wyszukiwarka
Podobne podstrony:
Wyznaczanie stałej reakcji szybkości zmydlania estru, Studia, Politechnika
Wyznaczanie stałej reakcji szybkości zmydlania estru, Studia, Politechnika
Wyznaczanie stałej szybkości reakcji zmydlania estru
Sprawozdanie - Kinetyka chemiczna. Wyznaczenie stałej szybkości, Studia, Chemia
chemia sprawko Wyznaczanie stałej szybkości reakcji
2003 chemia sprawko Wyznaczanie stałej szybkości reakcji
Wyznaczanie stalej szybkosci reakcji zmydlania octanu etylu metoda konduktometryczna DOC
Martynaa chemia sprawko Wyznaczanie stałej szybkości reakcji
chemia sprawko Wyznaczanie stałej szybkości reakcji
wyznaczanie stałej szybkosci rozpadu inicjatora metoda spektrofotometryczna
wyznaczanie stałej szybkosci rozpadu inicjatora metoda spektrofotometryczna 2003 excel
27 Wyznaczanie stałej szybkości i rzędu reakcji metodą graf
,chemia fizyczna, wyznaczanie stałej i stopnia dysocjacji słabych elektrolitów, Gr
wyznaczanie współczynników aktywności z pomiarów sem, Chemia fizyczna, laboratorium, Chemia fizyczna
Wyznaczanie stałej siatki dyfrakcyjnej, Prz inf 2013, I Semestr Informatyka, Fizyka, SPRAWOZDANIA DU
FIZYKA LABORATORIUM SPRAWOZDANIE Dyfrakcja światła Wyznaczenie stałej siatki dyfrakcyjnej w
20. Wyznaczanie stałej siatki dyfrakcyjnej, Inżynieria Środowiska PK, Semestr 1, Fizyka, Fizyka Labo
więcej podobnych podstron