STATYSTYKA
dr. Marcin Zawada
WYKŁAD 3:
ANALIZA WSPÓŁCZESNOŚCI CECH NIEMIERZALNYCH
W badaniach statystycznych niejednokrotnie zachodzi konieczność ustalenia skojarzeń między dwiema cechami X i Y z których obie (lub przynajmniej jedna ) mają charakter jakościowy , np. :
* miejsce zamieszkania - preferencje wyborcze
* płeć- zainteresowanie programami tv
* wykształcenie - źródła informacji o nowym produkcie.
W takim przypadku materiał statystyczny umieszczony w zbudowanej do tego celu tablicy wielodzielnej
o określonej liczbie kolumn i wierszy, w której zamieszczamy liczebność poszczególnych wariantów cech.
Yi Xi |
Y1 y2 …. y3 |
∑=nij=ni
|
x1
x2 . . .
Xr |
n11 n12 … n1s
n21 n22 …. n2s . . . . . . . . .
nr1 nr12…. nrs |
n1.
n2. . . .
nr. |
∑nji=n.j |
n.1 n.2 ….. n.s |
n |
TABELA KORELACYJNA :
2. Do badania współczesności dwóch cech zwłaszcza jakościowych wykorzystuje się miary zależności oparte na wartości statystyki chi kwadrat...
Miernik chi- kwadrat obliczmy z zależności:
nij- liczebności empiryczne
-//- - liczebności teoretyczne czyli takie jakie były , gdyby badane cechy były od siebie niezależne.
Liczebności teoretyczne obliczamy ze wzoru:
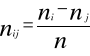
Jeżeli stwierdzimy, że między dwiema rozpatrywanymi cechami istnieje zależność
(wskazuje na to np. wysoka wartość X2)to należy ustalić siłę.
Do mierników siły opartych na mierniku x2 należy m.in. współczynnik zbieżności T Czuprowa
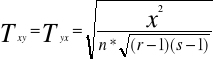
Współczynnik ten przyjmuje wartości z przedziału (0,1) T=0 gdy cechy są stochastycznie niezależne . Im bliższa jedności wartości tego miernika , tym silniejsza zależność między badanymi cechami gdy liczba kolumn jest znacznie większa lub mniejsza od liczby wiersza , maksymalna wartość T może być znacznie mniejsza od jedności (mimo silniejszego związku między cechami).
Przykład
W 600 osobowej losowo dobranej grupie ludzi przeprowadzono badania ankietowe mające na celu uzyskanie odp. na pyt. : ”Czy istnieje zależność między wykształceniem telewidzów a rodzajem programu, który najchętniej oglądają ?” Otzrymano następujące wyniki :
wykształcenie
|
Rodzaj programu
|
||||
|
Film
|
Teatr
|
Programy rozrywkowe
|
Programy publicystyczne
|
razem
|
Podstawowe |
105
|
10
|
75
|
10
|
200
|
Średnie
|
120
|
60
|
80
|
40
|
300
|
Wyższe |
35 |
30 |
15 |
20 |
100 |
Razem |
260 |
100 |
170 |
70 |
600 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
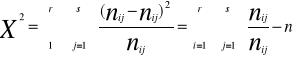
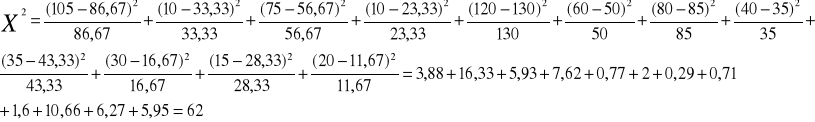
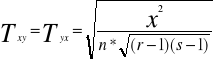
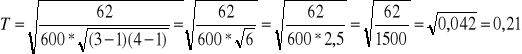
T2=(0,21)2*100%=4,41%
Odp:
Analiza współzależności zjawisk ekonomicznych
Współzależność między zmiennymi może być dwojakiego rodzaju : funkcyjna i stochastyczna (losowa)
Istota zależności funkcyjnej polega na tym , że zmiana wartości jednej zmiennej powoduje ściśle określone zmiany drugiej zmiennej, tak więc w zależności funkcyjnej określonej wartości jednej CX) odpowiada jedna i tylko jedna wartość drugiej zmiennej CY)
Zależność stochastyczna występuje wtedy gdy wraz ze zmianą jednej zmiennej zmienia się rozkład prawdopodobieństwa drugiej zmiennej. Szczególnym przypadkiem zależności stochastycznej jest zależność korelacyjna (statystyczna). Polega ona na tym , że określonym wartościom jednej zmiennej przyporządkowane są ściśle określone średnie wartości drugiej zmiennej. Możemy zatem ustalić jak zmieni się - średnio biorąc - wartość zmiennej zależnej Y w zależności od wartości zmiennej niezależnej X .
Badanie związków korelacyjnych ma sens jedynie wtedy , gdy między zmiennymi istnieje więź przyczynowo-skutkowa, dająca się logicznie wytłumaczyć.
Wśród związków przyczynowo-skutkowych można wyróżnić związki dwustronne i jednostronne . Związki dwustronne cechuje wzajemne oddziaływanie na siebie badanych zjawisk.
Często wykorzystywanym w praktyce sposobem stwierdzania czy istnieje korelacja między dwiema zmiennymi jest diagram punktowy zwany też diagramem korelacyjnym (korelagramem).
Sporządza się go w prostokątnym układzie współrzędnych odkładając na osiach wartości badanych zmiennych powstaje w ten sposób pewna „chmura”(smuga)punktów, która daje możliwość wstępnej oceny siły i kierunków zależności oraz może być podstawą wyboru określonej funkcji matematycznej opisującej zależności między badanymi zmiennymi (zależność liniowa lub nieliniowa)


1) y 2) y
x x
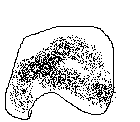

3) y 4
x x
Jeżeli wartości zmiennych w obydwu szeregach wykazują zmiany jednokierunkowe to mamy do czynienia z korelacją dodatnią (x ... ,y .... „t” ; .......) , gdy zaś wzrostem wartości jednego szeregu odpowiadają spadki wartości danych drugiego szeregu (zmiany różnokierunkowe), to między zmiennymi zachodzi korelacja ujemna.
To czy zmienne są korelowane i w jaki sposób orzekamy na podstawie korelacji (współzmienności). Parametr ten jest jednak wyrażony w jednostkach absolutnych (jest to iloczyn jednostek , w których mierzone są obie cechy i stąd nie jest możliwa na jego podstawie ocena intensywności korelacji ) .
cov(x,y) = cov (y,x)= ![]()
(xi - y)
Stopień zależności liniowej pomiędzy badanymi cechami mierzalnymi określany jest za pomocą współczynnika korelacji liniowej Pearsona .
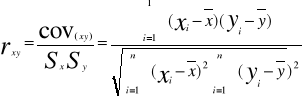
Przyjmuje on wartości z przedziału (-1,1).Jego znak informuje o kierunku korelacji a wartość o sile związku.
Kwadrat współczynnika korelacji liniowej nazywany współczynnikiem determinacji liniowej. Informuje o tym jaka część zmienności i zmiennej zależnej jest wyjaśniona przez zmienność zmiennej objaśniającej .
FUNKACJA REGRESJI
Funkcja regresji - to analityczny wyraz przyporządkowania średnich wartości zmiennej objaśnianej (zależnej) konkretnym wartościom zmiennych objaśniających (niezależnych) .
W naszych rozważaniach zajmiemy się metodami badania zależności między dwiema zmiennymi , które mają postać liniową .
Odpowiednio możemy wyznaczyć :
funkcje regresji zmiennej zależnej (objaśnionej) Y przy danych wartościach zmiennej niezależnej (objaśniającej) X .
y =ay + by +ey
funkcja regresji zmiennej X względem Y
![]()
e- składnik reprezentuje wpływ innych zmiennych na badane zjawisko
Parametry takich funkcji szcuje się KMNK (Klasyczna Metoda Najmniejszych Kwadratów)
po przyjęciu a następnie sprawdzeniu pewnych założeń.
W metodzie tej wartości parametrów funkcji regresji szacuje się z następujących zależności :
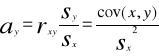
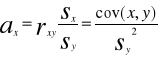
![]()
![]()
Wartości współczynników regresji ay i ax określają o ile jednostek przeciętnie wzrośnie (lub zmaleje gdy a...0 i a.....0) wartość zmiennej zależnej , gdy wartość zmiennej niezależnej wzrośnie o jedną jednostkę .
Parametry ay i bx rzadko mają sensowną interpretację ekonomiczną.
Y=3x+5 x=1 y 8 x=5y-1
X=2 y 11 x =-3x+5
X=3 y 14 x= -5y-1
Warto zauważyć , że między współczynnikami regresji a współczynnikami korelacji liniowej Pearsona zachodzi następująca zależność :
![]()
Współczynnik korelacji przyjmuje taki sam znak jaki mają współczynniki regresji. Współczynniki te obliczane z konkretnych informacji wyjściowych mają zawsze jednakowe znaki (albo obydwa dodatnie, albo obydwa ujemne).
Do badania korelacji w przypadku występowania skal porządkowych można używać dwóch miar : współczynnika korelacji rang Spermana i współczynnik korelacji rang Kendalla.
Współczynnik korelacji ran Spermana wyraża się zależnością :
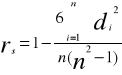
di- różnica między rangami cechy X i cechy Y
Obliczenia rozpoczyna się od uporządkowania wyjściowych informacji wg rosnących (lub malejących )wariantów jednej z cech. Uporządkowanym wartościom nadaje się numery kolejnych liczb naturalnych - czynność ta nazywa się rangowaniem. W przypadku gdy występuje jednakowe wartości realizacji zmiennych, przyporządkowujemy im średnią arytmetyczną obliczane z ich kolejnych numerów. Współczynnik ten przyjmuje wartości z przedziału (-1,1), a jego interpretacja jest identyczna jak współczynnika korelacji liniowej Pearsona.
PRZYKŁAD:
Wpływ przebiegu opon ( w tys km) na ich zużycie w %przedstawie funkcjia regresji postaci y=2,5+0,82x. Na podstawie badań technicznych 100 pojazdów ustalono,że średni przebieg opon wynosi 42 km. Średnie zużycie opon jest równe 11,8%. Współczynnik zmienności przebiegu opon wynosi 24%. Na podstawie danych oblicz silę i kierunek zależności pomiędzy badanymi zmiennymi. Jakiego zużycie opon należy oczekiwać- średnio biorąc przy przebiegu równym 46km2.
Y-zuzycie w %
X- przebieg w km
Y=25+0,82x
42tys km= ![]()
59,44% =![]()
11,8%=Sy
24% = Vx
Oblicz: r=?
![]()
![]()
![]()
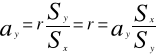
![]()
![]()
Odp: Między przebiegiem a zużyciem opon zachodzi zależność umiarkowana dodatnia. W 49% zużycie opon zależy od ich przebiegu
Y=? x=46tys
Y=25+0,82*46
Y=25+37,72
Y=62,72%
Opd: Przy przebiegu równym 46tys km2, średnie zużycie wyniesie 62,72%
![]()
Wyszukiwarka
Podobne podstrony:
x2, wykłady i notatki, statystyka matematyczna
Rozklad statystyk z proby, wykłady i notatki, statystyka matematyczna
ALGORYTM MNOŻENIA PISEMNE GO(1), wykłady i notatki, dydaktyka matematyki, matematyka przedszkole i 1
zbiory, wykłady i notatki, dydaktyka matematyki, matematyka przedszkole i 1-3
sprawdzzanie osiągnięć(1), wykłady i notatki, dydaktyka matematyki, matematyka przedszkole i 1-3
Działania na ułamkach, wykłady i notatki, dydaktyka matematyki, matematyka przedszkole i 1-3
wprowadzanie algorytmu odejmowqnia liczb w zakresie 1000(1), wykłady i notatki, dydaktyka matematyki
Metoda kr- cw, wykłady i notatki, dydaktyka matematyki, matematyka przedszkole i 1-3
Wprowadzenie algorytmu dodawania(1), wykłady i notatki, dydaktyka matematyki, matematyka przedszkole
Pojęcie algorytmu, wykłady i notatki, dydaktyka matematyki, matematyka przedszkole i 1-3
WPROWADZANIE GEOMETRII W KLASACH 1-3(1), wykłady i notatki, dydaktyka matematyki, matematyka przedsz
Boratyńska A Wykłady ze statystyki matematycznej
Wymagania odnośnie projektu na zaliczenie wykładu ze Statystyki matematycznej
karta kalendarz na matme, wykłady i notatki, dydaktyka matematyki, matematyka przedszkole i 1-3
ZEGAR - całość, wykłady i notatki, dydaktyka matematyki, matematyka przedszkole i 1-3
Mierzenie dlugosci, wykłady i notatki, dydaktyka matematyki, matematyka przedszkole i 1-3
więcej podobnych podstron