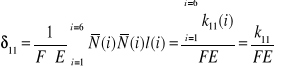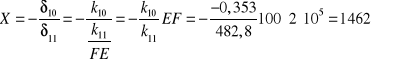Przykład 3 MB Kratownica

Obliczyć wartości sił w prętach kratownicy przedstawionej na rys.1. Pręt 2 został podgrzany o 20^oC. Kratownica zbudowana jest z 6 prętów o identycznym przekroju
, oraz z materiału, którego moduł Younga
, a współczynnik rozszerzalności liniowej
. Pręty 1, 3, 5, 6 mają identyczną długość
. Kratownicę podparto na dwóch podporach w węzłach 1 i 2. Pręt 3 jest w poziomie. Podpora przegubowa przesuwna daje reakcję o kierunku pionowym.

y 6

3 4

1 2 4 5

R_1y R_1x R₂

1 2 x Rys.1

3

Rozwiązanie

Z warunku równowagi całej konstrukcji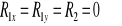

1. Sprawdzenie czy konstrukcja jest statycznie wewnętrznie wyznaczalna

Ilość węzłów
, ilość prętów
, wzór na sprawdzenie statycznej wyznaczalności
sprawdzenie
. Różnica między rzeczywistą ilością prętów p a ilością prętów p₁ przy której kratownica była by statycznie wyznaczalna, wynosi
. Wniosek kratownica jest jednokrotnie wewnętrznie statycznie niewyznaczalna.

2. Należy kratownice uczynić statycznie wyznaczalną np. odcinając myślowo pręt 4 od węzła 3. W miejscu myślowego przecięcia w rzeczywistej konstrukcji działa siła X , która zapewnia, że w miejscu tym będzie ciągłość konstrukcji czyli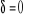
.

Równanie ciągłości konstrukcji w miejscu przecięcia pręta 4

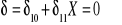
………………. ………………………………….(a)

Gdzie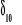
jest luką między węzłem 3 a końcem pręta 4 wywołaną działaniem temperatury powodującym wydłużenie pręta 2 o u(2) = l(2)tα_t (rys.2).

δ₁₀

y 6

3 4

1 2 4 5

R_1y R_1x R₂

1 2 x Rys.2

3 - 7 -

Natomiast δ₁₁ jest luką między węzłem 3 a końcem pręta 4 wywołaną wirtualnym obciążeniem o wartości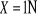
(rys.3).

δ₁₁

y 6

1[N] 4

3 1[N]

1 2 4 5

R_1y R_1x R₂

1 2 x Rys.3

3

3. Z warunku równowagi całej konstrukcji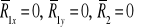

Z warunków równowagi poszczególnych węzłów kratownic zamieszczonych na rysunkach 2 i 3 obliczamy wartości sił działających w prętach. I tak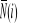
są siłami powstałymi w wyniku działania obciążenia wirtualnego (rys.3). Wartości tych sił oraz długości prętów i ich przyrosty wydłużenia u(i) spowodowanych wzrostem temperatury zamieszczono w tabeli 1.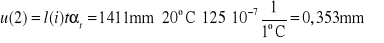

Tabela 1

i	1	2	3	4	5	6
u(i)mm	0	0,353	0	0	0	0
	0,707	-1	0,707	-1	0,707	0,707
l(i)cm	100	141,4	100	141,4	100	100

4. Wartości współczynników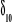
i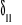
obliczamy ze wzorów:

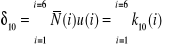
…………………………………………..(b)

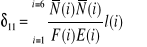
……………………………………………………...(c)

Ponieważ w naszym przypadku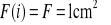
oraz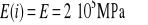
to wzór (b) przybierze postać

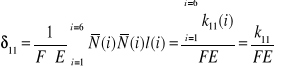
…………………………….(d)

W tabeli 2 zamieszczono wartości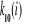
oraz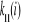

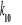
- 8 -

Tabela 2

i	1	2	3	4	5	6
k10(i)[N cm]	0	- 0,353	0	0	0	0
k11(i)[N cm]	50,0	141,4	50,0	141,4	50,0	50,0

obliczamy przez podstawienie danych z tabeli 1 do (c) stąd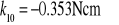

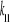
obliczamy przez podstawienie danych z tabeli 2 do (d) stąd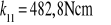

Z równania (a) mamy

Wartości rzeczywistych sił działających w konstrukcji przedstawionej na rys.1

obliczamy ze wzoru

Wartości sił w prętach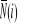
wywołanych obciążeniem wirtualnym podano w tabeli 1.

Wartości rzeczywistych sił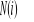
panujących w prętach przedstawiono w tabeli 3

Tabela 3

i	1	2	3	4	5	6
N(i)	1033	- 1462	1033	- 1462	1033	1033

Znak minus przy wartości siły, wskazuje że siła jest siłą ściskającą pręt.

- 9 -