1. Obliczyć na podstawie reguły de l' Hospitala następujące granice :a) 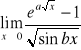
;
1. Obliczyć na podstawie reguły de l' Hospitala następujące granice :a) 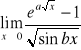
;
b) 
; c) ![]()
; d) 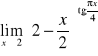
; e) ![]()
; f)![]()
g)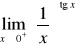
;h) ![]()
; i) ![]()
; j) ![]()
; k) 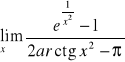
; l)![]()
. M) 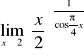
n) ![]()
.
Odp:a) ![]()
; b) ![]()
; c) ![]()
; d) ![]()
; e) 1; f) 1; g) 1; h) e; i) 1; j) ![]()
; k) ![]()
; l) 1.
2. Znaleźć asymptoty funkcji : a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f)![]()
g) ![]()
h) 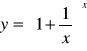
i) ![]()
j) ![]()
k) ![]()
.
3. Wykazać, że funkcja ![]()
, ![]()
jest stała
4. Sprawdzić, czy funkcje ![]()
są równe w przedziale
(-1 , 0 )
5.Obliczyć pochodne n-tego rzędu następujących funkcji :a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
; f) ![]()
6. Stosując wzór Leibniza-Newtona obliczyć pochodne funkcji: a)![]()
b) ![]()
c) ![]()
7.Sprawdzić, czy funkcja ![]()
spełnia na przedziale ![]()
założenia Tw. Lagrange'a ( to znaczy należy sprawdzić, czy funkcja jest ciągła i ma pochodną na przedziale)
8.Sprawdzić, czy funkcja 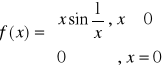
spełnia na przedziale ![]()
założenia Tw. Lagrange'a ( to znaczy należy sprawdzić, czy funkcja jest ciągła i ma pochodną na
9. Sprawdzić, czy funkcje : a) ![]()
w przedziale <1,e> ; b) ![]()
w przedziale <-1,1> spełnia założenia tw. Rolle'a.
10. Sprawdzić, czy funkcja ![]()
spełnia założenia tw. Lagrange'a w przedziale <0,2>
11.Napisać wzór Maclaurina dla funkcji : a) ![]()
b) ![]()
c) ![]()
d) ![]()
12. Napisać wzór Taylora rzędu n dla funkcji ![]()
i ![]()
13. Napisać wzór Taylora dla funkcji ![]()
w punkcie ![]()
14. Napisać wzór Maclaurina z resztą R3 dla funkcji ![]()
9. Oszacować bezwzględny błąd wzoru przybliżonego : a) ![]()
dla ![]()
;
b) ![]()
dla ![]()
. c)![]()
dla ![]()
; d) ![]()
dla ![]()
15.. Wykazać, że przy obliczaniu wartości funkcji ![]()
za pomocą wzoru przybliżonego![]()
dla ![]()
, popełniamy błąd mniejszy niż 0.006.
16. Oszacować dokładność wzoru przybliżonego ![]()
dla ![]()
17. Obliczyć ![]()
z dokładnością do 0,0001
18. Obliczyć : a) ![]()
z błędem bezwzględnym mniejszym niż 0,01 ; b) ![]()
z błędem bezwzględnym mniejszym niż 0,001
c) ln1,02 z błędem bezwzględnym mniejszym niż 0,00001.
Zadania domowe dotyczące wykładu 2
Obliczyć przybliżona wartość wyrażenia: a) ![]()
, b) arccos0,499
Korzystając z definicji uzasadnić, że podane funkcje mają ekstremum lokalne we wskazanych punktach
a) ![]()
, ![]()
, b) ![]()
, ![]()
3. Znaleźć wszystkie ekstrema lokalne funkcji
a) ![]()
, b) ![]()
, c) ![]()
, d) ![]()
4. Określić przedziały wypukłości i wklęsłości oraz punkty przegięcia funkcji
a) ![]()
, b) ![]()
c) ![]()
, d) ![]()
5. Zbadać i wykreślić funkcje
a) ![]()
, b) ![]()
, c) ![]()
, d)![]()
, e) ![]()
, f) ![]()