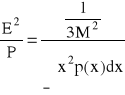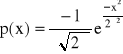
dla -∞ > x < ∞ .
Zadanie Z4/2.
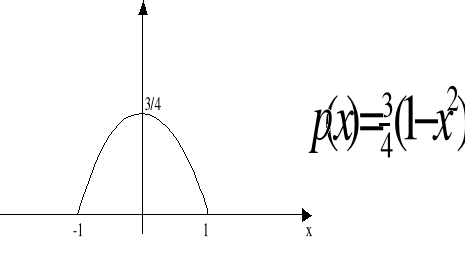
Sygnał losowy o gęstości prawdopodobieństwa opisanej funkcją Gausa:
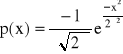
dla -∞ > x < ∞ .
jest podany kompresji z charakterystyką typu A ( A=87.6).
Dla jakiej wartości odchylenia standardowego δ stosunek mocy sygnału do mocy szumów kwantyzacji (P/![]()
) przy idealnym kwantowaniu logarytmicznym będzie taki sam jak przy kwantowaniu równomiernym?
1.Wstęp teoretyczny.
Moc sygnału jest równa:
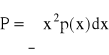
Moc szumów kwantyzacji w przypadku kwantowania równomiernego ( Wszystkie przedziały kwantowania mają jednakową szerokość - Jeśli zakres zmienności sygnału wyjściowego podzielimy na M części to szerokość jednakowych przedziałów kwantowania jest równa 2/M) wynosi:
![]()
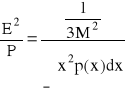
Dla kwantowania równomiernego stosunek mocy szumów kwantyzacji do mocy sygnału:
W przypadku nierównomiernego kwantowania sygnał analogowy poddaje się kompresji,a potem stosuje się kwantowanie równomierne.
Charakterystyka kompresji logarytmicznej typu A ma postać:
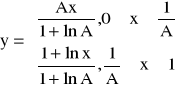
przy czym A przyjmuje się zwykle 87,6.
W przypadku dużej liczby poziomów kwantyzacji moc szumów kwantyzacji wyraża się wzorem:
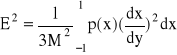
Ostatecznie dla charakterystyki typu A stosunek mocy szumów kwantyzacji do mocy sygnału:
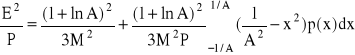
Pierwsza część po prawej stronie wyrażenia przedstawia stosunek szum/sygnał przy idealnym logarytmicznym kwantowaniu. Druga część odpowiada wzrostowi szumu spowodowanego nieidealnym kwantowaniem.
2.Rozwiązanie zadania.
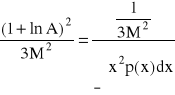
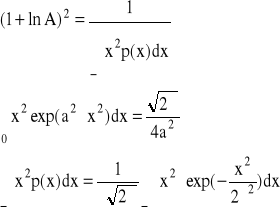
oraz ![]()
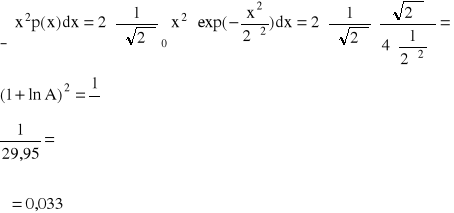
Treść zadania
Sygnał losowy o rozkładzie gęstości prawdopodobieństwa p(x) (rys.) jest sygnałem modulującym w systemie PCM. Dla jakiej wartości W moc szumu kwantyzacji E2 będzie taka sama przy kwantowaniu równomiernym i nierównomiernym z charakterystyką kompresji typu μ (μ=3)
p(x)
![]()
![]()
-W W x
2. Rozwiązanie
W systemach PCM przetwarzany sygnał jest poddawany procesowi kwantyzacji tzn. zakres zmiany amplitudy jest podzielony na M przedziałów i przesyłana jest tylko informacja o przedziale w którym występuje sygnał.
Wyróżniamy kwantyzację równomierną i nierównomierną. Wprowadzanie kwantyzacji nierównomiernej powoduje zmniejszenie szumu kwantyzacji ponieważ przy dużym prawdopodobieństwie wystąpienia sygnału szerokość przedziału się zmniejsz , a przy większym prawdopodobieństwie zwiększa.
Moc szumu kwantyzacji określamy następująco:
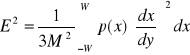
-dla kwantowania równomiernego:
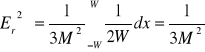
przy czym : p(x)=![]()
-dla kwantowania nierównomiernego:
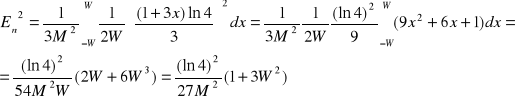
przy czym:
![]()
; ![]()
Z porównania obydwu mocy wynika:
![]()
czyli moce szumu kwantyzacji (równomiernego i nierównomiernego) będą sobie równe dla:
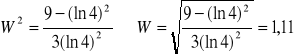
Treść zadania
Obliczyć wartość stałej XA, przy której zachodzi równość mocy szumów kwantyzacji dla sygnałów losowych o różnych gęstościach prawdopodobieństwa. Gęstość prawdopodobieństwa jednego z sygnałów jest funkcją stałą w przedziale <-XA,XA> równą 1/2XA, zaś drugiego opisana zależnością:
![]()
dla -B < x < B i B=3*104
Dla obu sygnałów stosuje się taką samą liczbę przedziałów i charakterystykę kompresji typu μ (μ=100).
Rozwiązanie
Aby obliczyć szukaną stałą policzę moce szumów kwantyzacji dla obu sygnałów (korzystając z podanego wyżej wzoru). Następnie porównam je i z otrzymanego równania wyznaczę stałą XA.
Ponieważ, obie gęstości są funkcjami parzystymi, więc całkowanie przeprowadzę tylko dla dodatnich wartości.
Moc szumów pierwszego sygnału:
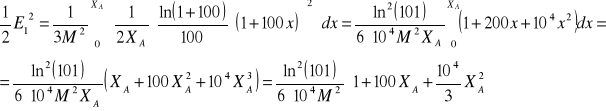
Moc szumów drugiego sygnału:
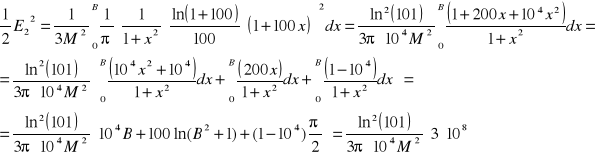
A więc skoro te moce są równe to:
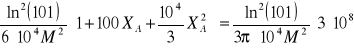
![]()
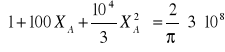
![]()
![]()
![]()
Otrzymałem równanie kwadratowe, które po rozwiązaniu dało mi szukaną wartość
XA = 239,35
Zadanie 4/6
Treść zadania:
Podane niżej sygnały mają pasmo nieograniczone. Można je jednak aproksymować sygnałami o ograniczonym paśmie. Przyjąć odpowiednie kryterium aproksymacji i znaleźć odpowiednią minimalną szybkość próbkowania (kryterium np. 0.95 energii)
e -2|t|
e -2t cos(100t)1(t)
te -t1(t)
Π (t/τ), τ = 20s
2) Wprowadzenie teoretyczne:
Minimalna częstotliwość próbkowania wynika z twierdzenia Shannona i jest zdefiniowana:
fp > fg
gdzie; fp - częstotliwość próbkowania:
fg - górna częstotliwość sygnału ( największa częstotliwość występująca w widmie)
Rozwiązanie:
Przykład a:
f(t) = e -2|t|
Czyli :
![]()
korzystając z kryterium 0,95 energii możemy napisać:
0,95 Et = Eω (1)
gdzie:
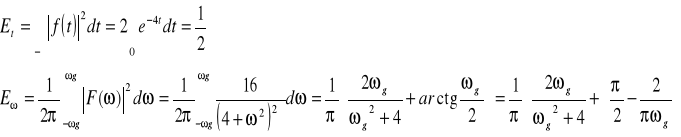
gdyż: 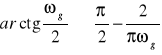
Korzystając ze wzoru (1) możemy napisać:
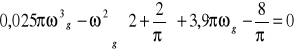
rozwiązaniem tego równania jest ωg = 5, fg = ωg /2π = 0,758Hz czyli fpmin = 1,591
Przykład b):
Wyznaczam energię sygnału:
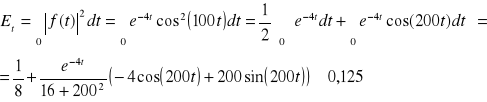
skorzystałem ze wzorów:
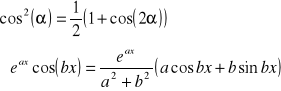
wyznaczam transformatę Fouriera sygnału:
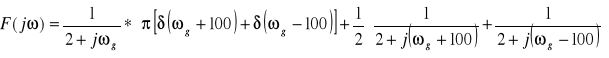
Po przekształceniu otrzymujemy:
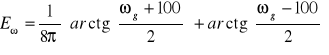
korzystając ze wzoru (1) otrzymujemy:
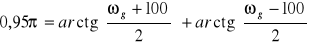
rozwiązaniem tego równania jest ωg = 113, fg = ωg /2π = 18,05Hz
czyli fpmin = 36,1Hz
Przykład c):
f(t) = te -t1(t)
w celu wyznaczenia transformaty Fouriera dla tego sygnału skorzystamy z zależności:
![]()
w wyniku otrzymujemy:
![]()
oraz: 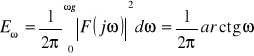
z kolei: 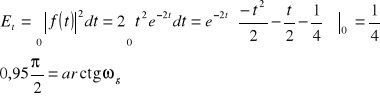
ωg =13,136, fg =2,092Hz, fpmin = 4,184 Hz
Przykład d):
Korzystając z symetrii transformaty Fouriera możemy napisać:
![]()
gdzie: ![]()
- sygnał bramkujący o szerokości τ
transformata ma postać: ![]()
tak więc otrzymujemy: 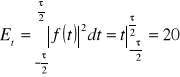
W celu obliczenia całki 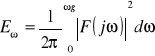
skorzystałem z programu MATHCAD, w wyniku otrzymałem: ![]()
ωg = 0,785, fg = 0,121Hz, fpmin =0,242