1. Zdefiniować moment siły względem punktu na płaszczyźnie oraz podać wzory do jego obliczenia.

Momentem wektora siły P względem punktu O nazywamy wektor M umiejscowiony w punkcie O prostopadły do płaszczyzny utworzonej przez siłę P i punkt O, którego moduł (wartość) jest równy iloczynowi modułów wektora siły P i wektora promienia r przez sinus kąta zawartego między tymi wektorami.

M = r x P

|M| = r P sin (r,P)

2. Podać różnicę między momentem siły względem punktu i momentem pary sił na płaszczyźnie.

Moment siły względem punktu: wartość liczbowa siły pomnożona przez ramię siły

Moment pary sił: działanie pary sil na bryłę; iloczyn wartości jednej z sił i ramienia pary; (wypadkowa wszystkich momentów)

3. Podać trzy zasady budowy układów geometrycznie niezmiennych na płaszczyźnie

• przegub rzeczywisty nie może znajdować się na kierunku pręta podporowego

• trzy przeguby nie mogą znajdować się na jednej prostej

• kierunki wszystkich prętów podporowych nie mogą przecinać siew jednym punkcie

Podać aksjomaty statyki

• ruch swobodnego ciała sztywnego nie ulegnie zmienia pod działaniem sił (dwóch) gdy siły te mają jednakowe moduły, kierunki i przeciwne zwroty

• ruch ciała sztywnego nie ulegnie zmianie jeżeli do działającego układu sił dodamy lub odejmiemy układ sił zerowych, zwany inaczej układem równowagi

• reguła równoległoboku: wypadkowa dwóch sił działających w jednym punkcie ciała sztywnego przyłożona jest w tym punkcie i jest siłą o module równym przekątnej równoległoboku opisanego tymi wektorami sił; leży na tej przekątnej i ma zwrot od A do B

• akcji i reakcji: siły, którymi działają dwa ciała na siebie mają jednakowe moduły, są skierowane wzdłuż jednej prostej i mają przeciwne zwroty

• zasada zesztywnienia: jeżeli ciało odkształcalne znajduje się w równowadze pod działaniem pewnego układu sił, to również pozostanie w równowadze ciało absolutnie sztywne pod działaniem tego samego układu sił;

warunki równowagi będące koniecznymi i wystarczającymi dla ciała sztywnego nie muszą być wystarczające dla odkształcalnego

• więzy: każde ciało nieswobodne można rozpatrywać jako ciało swobodne, jeśli myślowo uwolnimy go od więzów, zastępując działania więzów siłami więzów (reakcja bierna)

• Zdefiniować geometryczną zmienność układu płaskiego i podać przykłady

[jeżeli przegub wielokrotny łączy t tarcz, to ma 2(t-1) prętów podporowych; pojedyncza tarcza ma 3stopnie swobody, więc t tarcz ma 3t st.sw.] Warunek konieczny geometrycznej niezmienności: 3t<=p (p-liczba st.sw.odbieranych przez więzy); jeśli warunek nie jest spełniony: geometryczna zmienność (warunek dostateczny: kierunki wszystkich prętów podporowych nie mogą przecinać się w jednym punkcie, jeśli się przecinają - g. zmienność)

6. Zilustrować i opisać podporę płaską przegubową

Na podporze tej występuje jedna siła reakcji o znanym kierunku. Podpora ta odbiera ciału dwa stopnie swobody przez eliminację przesunięć w dwóch kierunkach. Zezwala tylko na obrót wokół punktu podparcia. Podporę tę można zastąpić dwoma prętami nierównoległymi, połączonymi w punkcie.

7. Zilustrować i opisać podporę płaską przegubowo - przesuwną

Na podporze tej występuje jedna siła reakcji o znanym kierunku, prostopadłym do płaszczyzny przesunięcia. Podpora ta odbiera cały jeden stopień swobody, gdyż eliminuje przesunięcie w jednym kierunku, a zezwala na przesunięcie w drugim kierunku i swobodny obrót. Podporę tę można zastąpić jednym prętem.

8. Zilustrować i opisać podporę płaską sztywno - przesuwną

9. Zilustrować i opisać podporę płaską sztywną

10. Zilustrować redukcję płaskiego zbieżnego układu sił oraz podać wzory końcowe

11. Zilustrować redukcję płaskiego równoległego układu sił oraz podać wzory końcowe

12. Zilustrować redukcję płaskiego dowolnego układu obciążeń oraz podać wzory końcowe

Przez redukcję układu sił rozumiemy przekształcenie układu w równoważny układ złożony z siły i pary sił (zastępujemy działanie układu sił jedną siłą i parą sił).
Rozważmy dowolny układ sił działających w jednej płaszczyźnie (rys.7.1) Proste działania sił Pi są dowolnie położone względem siebie na płaszczyźnie tzn. nie przecinają się w jednym punkcie. Zadajmy sobie pytanie przy jakich warunkach układ sił Pi da się zastąpić jednym z najprostszych układów sił, to jest dwójką zerową, jedną siłą  lub parą sił.
   W tym celu przeprowadzimy redukcję układu sił.
W płaszczyźnie działania siły obieramy dowolny punkt np. O, który nazywamy biegunem redukcji.
    Korzystamy z twierdzenia o równoległym przesuwaniu siły i przesuwamy siły P1 , P3, P4 do bieguna O. W ten sposób układ tych sił zaczepionych w punktach A, B, C , D przekształcilismy w układ równoważny, złożony z płaskiego Środkowego układu sił oraz układu czterech par sił.




Układ Środkowy zastąpimy jedną siłą S, gdy suma geometryczna sił Pi różna jest od zera, a układ par zastąpimy jedną parą o momencie równym algebraicznej sumie momentów par układu. Wektory momentów  poszczególnych par są równoległe, więc możemy je sumować algebraicznie. Zamiast obliczyć algebraiczną sumę momentów par układu, możemy obliczać algebraiczną sumę momentów względem bieguna O. Zatem w ogólnym przypadku układ sił Pi zastąpimy jedną siłą S, zaczepioną w biegunie O,
i parą sił o momencie:


         (1)

Siła S jest równa sumie wszystkich sił układu.
Geometryczną sumę sił układu, nazywamy wektorem głównym i oznaczamy Wg.
Sumę momentów sił Pi względem bieguna redukcji nazywamy momentem głównym i oznaczamy Mg.
Wartość wektora głównego Wg obliczamy, jako sumę wszystkich sił układu na osie odniesienia Ox i Oy.




Stąd otrzymujemy:




    Kierunek wektora głównego określamy, obliczając cosinus kąta, jaki prosta jego działania tworzy
z osią Ox :




    Dla układu płaskiego sił wartość momentu głównego na podstawie wzoru (1), jest równa sumie algebraicznej momentów sił składowych względem bieguna redukcji.




13. Zilustrować i podać wzory końcowe do wyznaczania wypadkowej dowolnego płaskiego układu obciążeń

14. Podać i opisać równania równowagi płaskiego zbieżnego i płaskiego równoległego układu sił

Pł. Zbieżny: układ sił, przyłożonych do ciała sztywnego, których kierunki działania leżą w jednej płaszczyźnie i przecinają się w jednym punkcie. Układ jest w równowadze, jeśli wypadkowa sił =0 (wektory sił tworzą wielobok zamknięty)




Równoległy:

15. Podać i opisać równania równowagi dowolnego płaskiego układu obciążeń




1. Aby płaski dowolny układ sił był w równowadze, sumy rzutów wszystkich sił na dwie osie układu współrzędnych i suma momentów tych sił względem dowolnego punktu płaszczyzny działania sił muszą być równe zeru.

2. Płaski układ sił jest w równowadze, jeżeli sumy momentów wszystkich sił względem trzech punktów nie leżących na jednej prostej są równe zeru.

16. Zdefiniować statyczną wyznaczalność układu płaskiego. Podać przykłady schematów SW

Są to układy, dla których z równań równowagi można jednoznacznie wyznaczyć siły reakcji. Dla takiego układu liczba reakcji jest równa liczbie niezależnych równań równowagi, oraz liczba stopni swobody, która zapewnia geometryczną niezmienność układu jest równa zero

17. Zdefiniować statyczną niewyznaczalność układu płaskiego. Podać przykłady schematów SN

Przypadek, gdy reakcji więzów układu nie da się wyznaczyć jedynie z samych równań statyki (równań równowagi, równań przegubów i twierdzenia o równoważności, w odniesieniu do układu o sztywnych tarcz) i niezbędne jest odwołanie się do odkształcalności układu; układy, dla których z równań równowagi otrzymuje się nieskończenie wiele rozwiązań na siły reakcji: liczba reakcji jest większa od liczby niezależnych równań równowagi, a liczba stopni swobody układu równa się zero

18. Zilustrować i opisać tarcie ślizgowe ciała, statyczne nierozwinięte i rozwinięte

Tarcie ślizgowe ciała występuje na styku dwóch ciał stałych gdy ciała przesuwają się względem siebie lub spoczywają względem siebie, a istnieje siła dążąca do przesunięcia ciał. (
). Jeżeli siła tarcia osiąga swą graniczną wartość, co oznacza, że tarcie jest całkowicie rozwinięte T_g=μN
                 

19. Zilustrować i opisać doświadczenia Coulomba i Morena oraz zdefiniować tarcie ślizgowe kinetyczne

Siła tarcia statycznego jest to reakcja styczna (styczna składowa całkowitej reakcji), przeciwstawiająca się przesunięciu ciał względem siebie.
Ogólnie zatem siłę tarcia można  zdefiniować jako siłę oporu, zapobiegającą ruchowi, który by powstał gdyby tarcia nie było. Jest więc to siła bierna, która wystąpi dla zachowania równowagi stykających się ciał.
Zależność między graniczną wartością siły tarcia, a naciskiem N okreŚlają prawa tarcia, ustalone na podstawie wielu doświadczeń wykonanych przez Coulomba i Morena dla różnego rodzaju stykających się powierzchni.
    1. Siła tarcia jest niezależna od wielkości powierzchni stykających się ze sobą ciał i zależy jedynie od
        ich rodzaju,
    2.WartoŚć siły tarcia dla ciała znajdującego się w spoczynku może zmienić się od zera do granicznej
       wartości, proporcjonalnej do całkowitego nacisku normalnego,
    3. W przypadku, gdy ciało Ślizga się po pewnej powierzchni, siła tarcia jest zawsze skierowana przeciwnie do kierunku ruchu i jest mniejsza od granicznej wartości.
Na podstawie tych praw można określić zależności między siłą tarcia T, a naciskiem normalnym N.
    Największa wartość siły przesuwającej, która przy danym nacisku jeszcze nie naruszy stanu względnego spoczynku, jest równa tak zwanej rozwiniętej siły tarcia statycznego Tst.max (rys. 10.1).                                                                 




gdzie:
N - jest reakcją normalną,
 - jest tak zwanym współczynnikiem tarcia statycznego.
Ciała pozostają w stanie równowagi względnej, dopóki siła styczna P nie przekroczy wartoŚci rozwiniętego tarcia statycznego, to jest gdy:


 

20. Zilustrować i opisać opór toczenia ciała, statyczne nierozwinięty i rozwinięty

21. Zilustrować tarcie ślizgowe cięgna ruchomego o krążek nieruchomy i podać wzór końcowy

22. Zilustrować tarcie ślizgowe cięgna nieruchomego o krążek ruchomy i podać wzór końcowy

23. Zilustrować i opisać podporę przestrzenną przegubową

24. Zilustrować i opisać podporę przestrzenną przegubowo - przesuwną w płaszczyźnie

25. Zilustrować i opisać podporę przestrzenną przegubowo - przesuwną w kierunku osi

26. Zilustrować i opisać podporę przestrzenną sztywną

27. Zilustrować moment siły względem punktu w przestrzeni oraz podać wzory do jego obliczania

28. Zilustrować moment siły względem osi ukośnej w przestrzeni oraz podać wzory do jego obliczania

29. Zilustrować i opisać przypadki szczególne momentu siły względem osi x w przestrzeni

30. Podać różnicę między momentem siły względem punktu i momentem siły względem osi w przestrzeni

M. względem punktu: długość ramienia razy wartość wektora

M. względem osi: równy jest rzutowi wektora momentu siły na prostą (oś)

31. Zilustrować redukcję przestrzennego zbieżnego układu sił oraz podać wzory końcowe

32. Zilustrować redukcję przestrzennego równoległego układu sił oraz podać wzory końcowe

33. Zilustrować redukcję dowolnego przestrzennego układu obciążeń oraz podać wzory końcowe

W celu przeprowadzenia redukcji przestrzennego dowolnego układu sił, przyjmijmy bryłę, na którą działa ten układ sił. Redukcję przeprowadzimy na układzie np. trzech sił P1, P2, P3, zaczepionych w punktach A, B, C (rys. 8.1).




    Obieramy dowolny biegun redukcji w punkcie O. Następnie do punktu O przesuwamy równolegle dwie siły (korzystamy z twierdzenia o równoległym przesuwaniu siły). W tym celu w biegunie O przykładamy dwójki zerowe o siłach równych siłom P1, P2, P3. W ten sposób otrzymujemy układ sił Pi, zaczepionych w biegunie redukcji, oraz układ trzech par sił działających w różnych płaszczyznach.
    Pary te powstają z sił Pi (P1, P2, P3 ), działających na bryłę, i z sił wchodzących w skład dwójek zerowych, zaczepionych w punkcie O. Dodając geometrycznie siły P1, P2, P3, otrzymujemy siłę S, równą geometrycznie wektorowi głównemu Wg. Pod względem wartości, kierunku i zwrotu, wektor główny Wg nie zależy od obioru bieguna redukcji  i dlatego jest niezmiennikiem układu.
Zatem układ trzech par sił, działających w różnych płaszczyznach, możemy zastąpić jedną parą, której  moment równy jest geometrycznej sumie par składowych. Momenty tych par są równe momentom sił P1, P2, P3, zaczepionych odpowiednio w punktach A, B, C, względem przyjętego bieguna redukcji.
Na rys.a) momenty tych par przedstawiono umownie jako wektory M1, M2, M3. Wektory momentów tych par są prostopadłe do płaszczyzn działania odpowiednich par.
Wektor, będący sumą geometryczną momentów par układu, nazywamy momentem głównym Mg.
    Powyższe postępowanie doprowadziło do zastąpienia dowolnego układu siłą S równą wektorowi głównemu Wg, oraz parą sił o momencie równym momentowi głównemu Mg.
WartoŚć wektora głównego wyznaczamy z następujących wzorów:




Kierunek wektora głównego wyznaczamy z następujących wzorów:


Pomiędzy cosinusami tych kątów zachodzi związek:




Wartość momentu głównego wyznaczamy ze wzorów:




Kierunek momentu głównego wyznaczamy ze wzorów:


Pomiędzy cosinusami tych kątów zachodzi związek:




Kąt  zawarty pomiędzy wektorem głównym Wg, a momentem głównym Mg obliczamy, korzystając z iloczynu skalarnego wektorów Wg i Mg.

34. Podać warunek redukcji przestrzennego układu obciążeń do wypadkowej, zilustrować wypadkową oraz podać końcowe wzory do jej wyznaczania

35. Podać warunek redukcji przestrzennego układu obciążeń do skrętnika, zilustrować skrętnik oraz podać wzory końcowe do jego wyznaczania

36. Podać i opisać równania równowagi przestrzennego zbieżnego i równoległego układu sił

Przestrzenny zbieżny: Aby były w równowadze, sumy rzutów tych sił na osie układu współrzędnych muszą być równe zero.




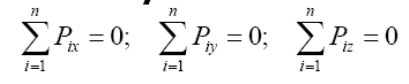
Równoległy:

37. Podać i opisać równania równowagi dowolnego przestrzennego układu obciążeń




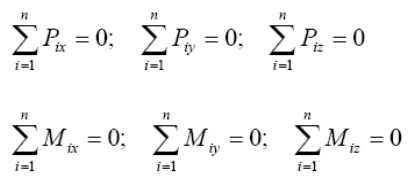
1. Aby dowolny układ sił był w równowadze, warunkiem koniecznym i wystarczającym jest, by suma sił i suma momentów względem dowolnego punktu były równe zeru.

2. Aby dowolny układ sił był w równowadze, sumy rzutów wszystkich sił na trzy osie układu współrzędnych oraz sumy momentów wszystkich sił względem tych osi muszą być równe zeru.

38. Zdefiniować środek ciężkości ciała sztywnego, podać warunek do jego wyznaczenia oraz wzory na jego współrzędne

Środek ciężkości jest to punkt położenia wypadkowej siły ciężkości układu lub ciała materialnego

Dla układu punktów materialnych:

Wektor wodzący
środka ciężkości C:




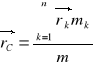
Współrzędne środka ciężkości C w prostokątnym układzie współrzędnych:

Dla ciał o ciągłym rozmieszczeniu masy:

Wektor wodzący środka ciężkości:




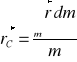
Współrzędne prostokątne środka ciężkości:

Jeżeli bryła jednorodna ma płaszczyznę, oś lub środek symetrii, to środek ciężkości będzie leżał na płaszczyźnie, osi lub w środku symetrii.

Środek ciężkości powierzchni jednorodnej.

Występujące w tych wzorach całki są całkami powierzchniowymi rozciągniętymi na całą powierzchnię F.

Środek ciężkości linii jednorodnej.

gdzie L jest długością linii.

---