Politechnika Zielonogórska

Instytut Robotyki i Inżynierii Oprogramowania

Laboratorium:

Algorytmy i struktury danych

Studia zaoczne

ćwiczenie 3:

Wybrane metody sortowania 2

1 Wstęp

1 Wstęp

Ćwiczenie ma na celu zapoznanie studentów z wybranymi metodami sortowania. Badane w ćwiczeniu metody sortowania to: sortowanie stogowe oraz sortowanie przez scalanie.

2. Metody sortowania:

2.1. Sortowanie szybkie (Quick Sort)

Jest to metoda, w której stosuje się zasadę zamiany. W metodzie sortowania szybkiego korzysta się z faktu, że w celu zapewnienia efektywności powinno się wymieniać obiekty położone daleko od siebie. Załóżmy że dane jest n obiektów ustawionych w odwrotnym porządku kluczy. Można posortować je wykonując tylko n/2 wymian, biorąc najpierw obiekty - skrajny z lewej strony i skrajny z prawej strony, a następnie posuwać się stopniowo do środka z obu stron. Oczywiście takie postępowanie możliwe jest tylko dlatego, że uporządkowanie było dokładnie odwrotne.

Wybierzmy losowo jakiś obiekt i nazwijmy go x; przeglądajmy tablicę od lewej strony aż znajdziemy obiekt ai > x, a następnie przeglądajmy tablicę od prawej strony aż znajdziemy aj < x. Wymieńmy teraz te dwa obiekty i kontynuujmy proces “przeglądania i zamiany”, aż nastąpi spotkanie gdzieś w środku tablicy. W rezultacie otrzymamy tablicę podzieloną na lewą część z kluczami mniejszymi od x oraz prawą część z kluczami większymi od x.

Jeżeli na przykład za x wybierzemy środkowy klucz 42, to w tablicy kluczy

44 55 12 42 94 6 18 67

trzeba dokonać dwóch wymian aby otrzymać tablicę podzieloną

18 6 12 42 94 55 44 67

Ostatnie wartości indeksów są i = 5 oraz j = 3. Klucze a1...ai-1 są mniejsze bądź równe kluczowi x=42, klucze aj+1...an są większe bądź równe temu kluczowi. Wynika stąd, że otrzymaliśmy podział na dwie części, a mianowicie

ak.klucz x.klucz dla k = 1...i-1

ak.klucz x.klucz dla k = j+1...n

oraz

ak.klucz = x.klucz dla k = j+1...i-1

Następnie powtarzamy tę operacje dla obu wcześniej utworzonych podciągów.

Algorytm

Istnieje ciąg liczb x_l, x_l+1, x_p,

Krok1. Przyjmij za element podziału element v znajdujący się w pobliżu środka ciągu, i podziel tym elementem dany ciąg.

Oznacza to, że v znajdzie się na pozycji elementu x_k, dla pewnego k spełniającego

l ≤ k ≤ p, i elementy na lewo będą od niego nie większe a elementy na prawo od niego będą nie mniejsze.

Krok 2. Zastosuj ten sam algorytm do (l, k-1, x)

Krok 2. Zastosuj ten sam algorytm do (k+1, p, x)

Algorytm ten jest bardzo prosty i efektywny, ponieważ zmienne i, j oraz x mogą być w czasie przeglądania tablicy trzymane w szybkich rejestrach maszyny cyfrowej.

2.2 Sortowanie stogowe

Stóg definiujemy jako ciąg kluczy : h1, hi+1, .., hp takich, że hi h2i , hi h2i+1 dla wszystkich i=l..p/2. Jeżeli drzewo binarne jest reprezentowane przez tablicę pokazaną na rys. 1a,

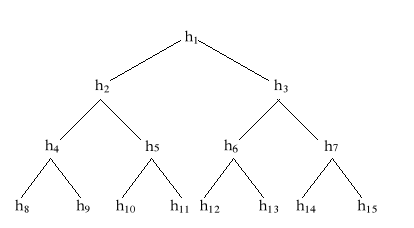
Rys1a Tablica przedstawiona jako drzewo binarne

wynika stąd, że posortowane drzewa z rys.1b i rys.1c są stogami, a w szczególności, że obiekt h1 jest najmniejszym elementem stogu h1 = min(h1...hn).

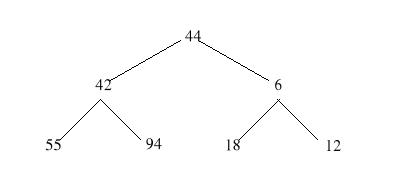
Rys 1b Stóg siedmioelementow1y

Weźmy na przykład stóg h1 ... h7 pokazany na rys. 1b i rozszerzmy go “na lewo” o obiekt h1=44. Nowy stóg otrzymujemy wstawiając najpierw obiekt x na wierzchołek drzewa, a później “przesiewając” go przez węzły mniejszych elementów stogu, które podnoszą się dzięki temu do góry. W podanym przykładzie liczba 44 jest przestawiana najpierw z liczbą 6, a następnie z liczbą 12 tworząc w ten sposób drzewo pokazane na rys. 1c.

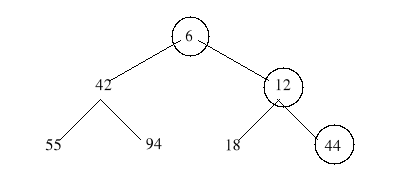
Rys 1c Przesiewanie elementu 44 przez stóg

ALGORYTM PRZESIEWANIA :

Zakładamy, że i, oraz j są parą indeksów wskazujących na elementy, które mają być zamienione podczas każdego kroku przesiewania.

Procedure przesiewanie (l,p:indeks);

Label 13;

Var i,j:indeks; x:obiekt;

Begin

i:=l: j:=2*i; x:=a[i];

while j p do begin

if a[j].klucz > a[j+1].klucz then j:=j+1;

if x.klucz a[j].klucz then goto 13;

a[i]:=a[j]; i:=j; j:=2*i;

end;

13: a[i]:=x;

End;

Dana jest tablica h1...hn; jej elementy hn/2...hn tworzą już stóg, ponieważ nie ma takich dwóch indeksów i,j, że j = 2i (lub j =2i+1). Obiekty te tworzą to, co można uważać za dolny wiersz odpowiedniego drzewa binarnego (rys. 1a) i nie musi między nimi zachodzić żadna reakcja. Stóg rozszerzamy obecnie na lewo. W każdym kroku jest dołączany nowy obiekt i ustawiany prawidłowo dzięki przesiewaniu.

W rezultacie, proces tworzenia stogu n-elenentowego h1...hn in situ jest opisany następująco :

l:=(n div 2)+1

while l > 1 do begin

l:=l-1; przesiewanie(l,n);

end;

W celu posortowania elementów stogu, trzeba teraz wykonać n kroków przesiewania, w każdym kroku należy zdjąć ze stogu jego ostatni element, powiedzmy x, przechować wierzchołkowy element w zwolnionym przez x miejscu i przesiać x na właściwe miejsce. Do posortowania elementów potrzebnych jest n-1 kroków. Proces ten jest opisany następująco :

p:=n;

while p > 1 do begin

x:=a[1]; a[1]:=a[p]; a[p]:=x;

p:=p-1;

przesiewanie(l,p);

end;

2.3 Sortowanie przez scalanie

Scalanie dwóch ciągów uporządkowanych w jeden ciąg uporządkowany może być wykonane w bardzo prosty sposób: patrzymy na początki danych ciągów i do tworzonego ciągu przenosimy mniejszy z elementów czołowych lub którykolwiek z ciągówz nich gdy sa równe. Ilustruje to Rys 2a

Rys 2a Przykład scalanie dwóch ciągów uporządkowanych

Kolejność przenoszenia elementów z ciągów do ciągu uporządkowanego zależy od ich wartości, które mogą powodować, że jeden z ciągów będzie znacznie prędzej przeniesiony niż drugi.

ALGORYTM SCALANIA DWÓCH CIĄGOW UPORZĄDKOWANYCH :

Dane: Dwa ciągi uporządkowane x i y.

Wynik: Uporządkowany ciąg wyjściowy z.

Krok 1: Dopóki oba ciągi x i y nie są puste wykonuj co następuje:

Przenieś najmniejszy z elementów ciągów x i y do ciągu z.

Krok 2: Do końca ciągu z dopisz elementy pozostałe w jednym z ciągów x lub y.

Algorytm scalania dwóch uporządkowanych ciągów można zastosować do tworzenia uporządkowanego ciągu z podciągów już uporządkowanych. A czy można go zastosować do porządkowania dowolnych ciągów? Tak - jeśli potrafimy je najpierw uporządkować. A czy można je uporządkować tą samą metodą? Można. Dochodzimy w ten sposób do metody porządkowania ciągu, która na zasadzie dziel i zwyciężaj, scala dwa prawie równoliczne podciągi, uporządkowane tą sama metodą. Działanie tej metody można prześledzić na rysunku 2b.

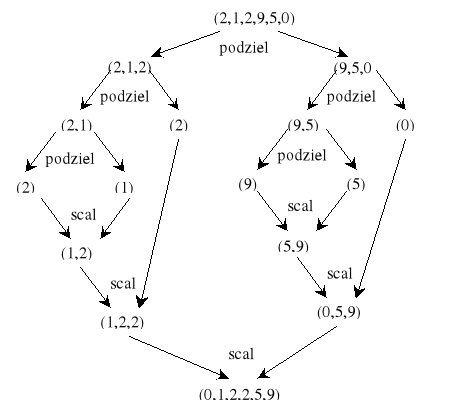
Rys 2b Przykład działania algorytmu porządkowania przez scalanie

Z powyższego szkicu oraz ilustracji wynika, że ciąg jest dzielony w każdym kroku na dwa niemal równoliczne podciągi, które rekurencyjnie porządkowane są tą sama metodą. Warunkiem zakończenia rekurencji w tym algorytmie jest sytuacja kiedy ciąg ma tylko jeden element. Zatem powrót z wywołań rekurencyjnych rozpoczyna się z ciągami złożonymi z pojedynczych elementów, które są następnie scalane w ciągi o długości dwa, a następnie w ciągi o długości trzy lub cztery elementy itd.

ALGORYTM PORZĄDKOWNIA PRZEZ SCALANIE:

Dane: Ciąg liczb x_l, x_l+1,..., x_p,.

Wynik: Uporządkowanie ciągu od najmniejszej do największej.

Krok 1: Przyjmij s:= (l + p) div 2 i wykonaj co następuje

Krok 2: Zastosuj ten sam algorytm dla (l, s, x).

Krok 3: Zastosuj ten sam algorytm dla (s + l, p, x).

Krok 4 Zastosuj algorytm scalania do powstałych ciągów.

Zadania do wykonania

1. Napisać schemat blokowy i zaimplementować metody sortowania szybkiego i stogowego dla tablicy z poprzedniego ćwiczenia. Program powinien podawać ilość porównań, ilość przestawień i czas sortowania.

2. Napisać program tworzący plik o rozmiarze około 3 MB składający się z uporządkowanych losowo liczb całkowitych, a następnie program sortujący ten plik przy pomocy metody sortowania przez scalanie.

---