M2 - Wargacki A. ; Nieścioruk M. ; sem.I, stopień II

Zadanie 8

Twierdzenie CASTIGLIANO (omówić + wzorki)

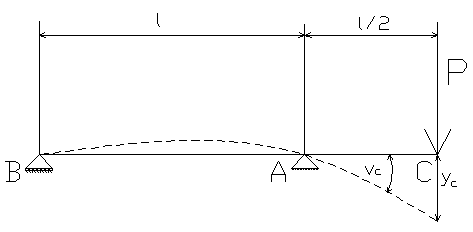
Wyznaczyć dla belki pokazanej na rysunku i obciążonej siłą P, przemieszczenia w punkcie C:

• ugięcie w punkcie C - y_c

• 
  kąt ugięcia (kąt obrotu) w punkcie C - v_c

Wprowadzam siłę dodatkową M_f=0.

Oznaczam reakcje R_A i R_B.

Oznaczam przedziały nieciągłości do późniejszych obliczeń.

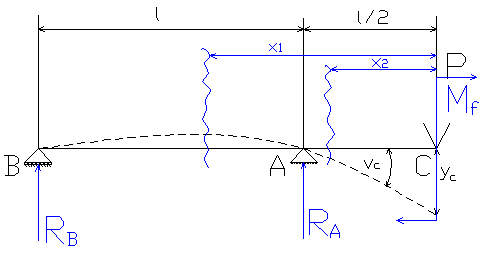
Rozwiązuję równania statyki i wyznaczam wartości reakcji w podporach:

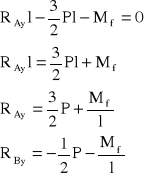
Wyznaczam wartości momentów gnących w przedziałach x₁ i x₂:

Obliczam pochodne cząstkowe momentów gnących w poszczególnych przedziałach po sile P:

Wykorzystując twierdzenie Castigliano obliczam ugięcie belki w punkcie C:

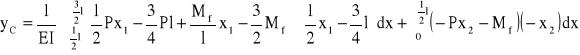
Wartość momentu M_f przyrównuję do zera i otrzymuję równanie:

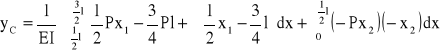
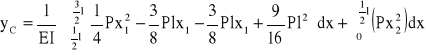
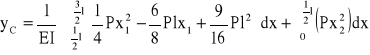
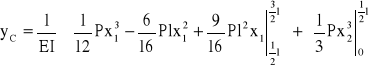
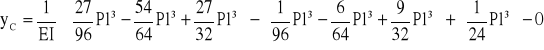
Otrzymuję wartość ugięcia belki w punkcie C:

Obliczam pochodne cząstkowe momentów gnących w poszczególnych przedziałach po momencie M_f:

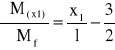
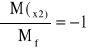
Wykorzystując twierdzenie Castigliano obliczam kąt ugięcia belki w punkcie C:

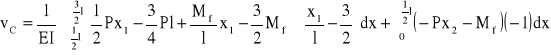
Wartość momentu M_f przyrównuję do zera i otrzymuję równanie:

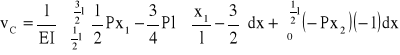
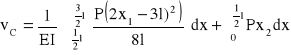
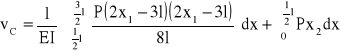
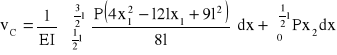
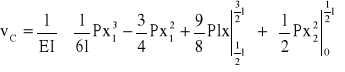
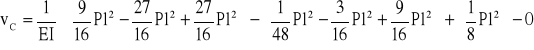
Otrzymuję wartość kąta ugięcia belki w punkcie C: