POLITECHNIKA BIAŁOSTOCKA
KATEDRA KONSTRUKCJI BETONOWYCH
Referat z ćwiczeń
Konstrukcje Betonowe
na temat
PRZEKRÓJ PROSTOKĄTNY
POJEDYŃCZO ZBROJONY
Joanna Lichota
Andrzej Leonczuk
KBI sem. VII
rok akad. 1999/2000
Fazy wytężenia przekrojów zginanych.
Za żelbetowy element zginany uważa się taki ustrój prętowy, płytowy lub tarczowy, w którym udział momentu zginającego jako wewnętrznej siły przekrojowej decyduje o rozkładzie naprężeń oraz o sposobie zniszczenia elementu. Typowymi przykładami elementów zginanych są belki, rygle ram oraz płyty jedno i dwukierunkowo zbrojone. Podstawowym kryterium uznania elementu zginanego za żelbetowy jest warunek minimalnego stopnia zbrojenia ρ, w odniesieniu do przekroju użytecznego elementu. Jeżeli warunek minimum zbrojenia nie jest spełniony, element należy uważać za betonowy. Zachowanie się zginanego elementu zbrojonego poddanego działaniu naprężeń pochodzących od momentu zginającego można prześledzić na przykładzie jednoprzęsłowej, wolnopodpartej belki obciążonej pojedynczą siłą skupioną, jak pokazano to na rysunku.
Prostoliniowy kształt wykresu momentów zginających oraz pominięcie wpływu ścinania na długości belki ułatwia zrozumienie mechanizmu zmian, jakie w różnych przekrojach belki wywołują naprężenia normalne pochodzące od zginania. W okolicach strefy podporowej, gdzie wartości momentów zginających są niewielkie pracuje cały przekrój betonowy (strefa ściskana i rozciągana). Ponieważ naprężenia rozciągające nie przekroczyły jeszcze wytrzymałości betonu na rozciąganie oznacza to, że belka jeszcze nie poddana została zarysowaniu. Ten sposób zachowania się belki bez rys określa się jako I fazę pracy przekroju.
Faza I pracy przekroju
W tym obszarze elementu można także wyróżnić fazę Ia, w której wykres naprężeń na wysokości belki jest liniowy, natomiast odkształcenia betonu są niewielkie (nie przekraczają 0,05 %o). W fazie tej ma miejsce zatem stała wartość współczynnika odkształcalności podłużnej betonu EC, równa jego wartości początkowej EC0 Przy nieco wyższych naprężeniach normalnych przekroje belki znajdują się w fazie Ib, której cechą charakterystyczną jest krzywo liniowość wykresu naprężeń w betonie strefy rozciąganej. Występuje to przy odpowiednio wyższych odkształceniach betonu rzędu 0,15%o. Wykres naprężeń w strefie ściskanej w fazie Ib jest nadal prostoliniowy, zaś naprężenia w betonie
strefy ściskanej znacznie mniejsze od wytrzymałości betonu na ściskanie. W przekrojach elementu zginanego pracujących w fazie I, na skutek małych odkształceń zachodzi pełna współpraca stali i betonu rozciąganego a także zachowana jest zasada płaskich przekrojów.
Faza I kończy się w tym przekroju belki, w którym naprężenie w betonie strefy rozciąganej, równe jest wytrzymałości betonu na rozciąganie, co skutkuje powstaniem pionowej rysy w przekroju. Fazę zarysowania przekrojów definiuje się jako II fazę pracy ustroju zginanego.
Faza II pracy przekroju
W przekrojach zarysowanych znacznie zwiększa się udział zbrojenia rozciąganego pracy przenoszeniu obciążenia, które musi tu równoważyć udział betonu ściskanego. Daje się zauważyć ponadto znaczne podniesienie osi obojętnej w przekrojach tego obszaru belki. Początkowo, w fazie IIa zasięg rys pionowych nie jest znaczny a wykres naprężeń w strefie ściskanej jest nadal zbliżony do liniowego. Powyżej rysy aż do osi obojętnej beton rozciągany nadal pracuje, chociaż jego udział w przenoszeniu naprężeń od zginania jest już niewielki. Przy odpowiednio wyższych naprężeniach, w fazie oznaczonej jako IIb zasięg rys prostopadłych do osi belki jest już znacznie wyższy, wykres naprężeń na wysokości strefy ściskanej jest wyraźnie krzywoliniowy a zbrojenie przenosi tu praktycznie całość naprężeń rozciągających. Faza IIb rozciąga się na te obszary belki, które jeszcze nie uległy zniszczeniu. Z rysunku widać, że w przekrojach między rysami belka zachowuje się tak, jak w fazie I, co oznacza, że nadal zachodzi tam współpraca betonu i zbrojenia.
Faza III pracy przekroju
Wraz z końcem fazy IIb, w miejscu zarysowania i pełnego wyczerpania nośności belka wchodzi w fazę III będącą fazą zniszczenia. Obszar ten jest rodzajem przegubu plastycznego w belce wolnopodpartej. Mechanizm zniszczenia belki w tym obszarze może być dwojakiego rodzaju. Zniszczenie może nastąpić albo przez wyczerpanie nośności zbrojenia rozciąganego czyli osiągnięcie wytrzymałości stali na rozciąganie bez jednoczesnego wyczerpania nośności strefy ściskanej (ang. "tension failure"), lub też przez wyczerpanie nośności strefy ściskanej betonu bez osiągnięcia granicy plastyczności stali rozciąganej (ang. " compression failure"). Zniszczenie elementów zgodnie z mechanizmem drugiego rodzaju jest w elementach zginanych niedopuszczalne, z uwagi na to, że stal jest tu nie w pełni wykorzystana a samo
zniszczenie może mieć charakter kruchy, to jest może nastąpić nawet bez wyraźnie zauważalnych rys pionowych. Może to być związane z niewielkimi wartościami odkształceń w zbrojeniu rozciąganym. W przypadku elementów zginanych wyeliminowanie takiego mechanizmu zniszczenia następuje poprzez obliczeniowe ograniczenie wysokości strefy ściskanej elementów zginanych. Wykres naprężeń w betonie na wysokości strefy ściskanej w fazie III (fazie zniszczenia) jest krzywoliniowy, zgodnie z zasadami wynikającymi z właściwości betonu. Przekrój odkształcony w fazie III jest w rzeczywistości zdeplanowany, jednakże dla celów obliczeń możliwe jest pominięcie tego efektu i przyjęcie przekroju płaskiego. W stosowanych dotąd metodach obliczeń zachowanie się żelbetowego przekroju
zginanego w fazie IIb (z uproszczeniem polegającym na przyjęciu liniowości naprężeń w strefie ściskanej) było podstawą metody klasycznej zwanej metodą naprężeń liniowych. Metoda ta w aktualnej normie PN-99 jest zalecana do obliczeń przekrojów w stanie granicznym użytkowalności. Zachowanie się przekroju w fazie III (z uproszczeniem
polegającym na zamianie w strefie ściskanej wykresu krzywoliniowego naprężeń na wykres prostokątny) jest natomiast podstawą metod analizy nośności, wprowadzanych do kolejnych edycji polskich norm począwszy od roku 1956.
Nośność elementów zginanych
Zasady ogólne obliczeń.
Zgodnie z postanowieniami Eurokodu 2 i normy PN-99 do wymiarowania żelbetowych przekrojów zginanych można wykorzystywać dwie metody:
metodę ścisłą,
metodę uproszczoną.
W metodzie ścisłej wykorzystuje się model odkształceniowy oparty na założeniach:
założenie płaskich przekrojów, zgodnie z zasadą Bernoulli'ego, co oznacza, że odkształcenia włókien przekroju są proporcjonalne do ich odległości od osi obojętnej,
Równość odkształceń w stali zbrojeniowej εś i otaczającym betonie εc na styku obu materiałów,
Pominięcie wytrzymałości betonu na rozciąganie fct, z uwagi na zarysowanie przekrojów,
Obliczeniowe związki σ − ε dla betonu pozwalające określić rozkłady naprężeń σc w strefie ściskanej betonu oraz ich wypadkową,
Obliczeniowe związki σ − ε dla stali zbrojeniowej w analizowanym przekroju.
W ogólnym przypadku przekroju elementu, który może być poddany zginaniu dwukierunkowemu względem osi x i y, z jednoczesnym udziałem sił podłużnych ( ściskanie lub rozciąganie ) graniczne nośności przekrojów normalnych w powyższym modelu obliczeniowym ustala się odpowiednio do stadium pracy elementu wykorzystując następujące zależności:
równania równowagi momentów i sił podłużnych w przekrojach normalnych z uwzględnieniem wypadkowych naprężeń w strefie ściskanej betonu oraz wypadkowych naprężeń w zbrojeniu podłużnym elementów,
równania określające zależności pomiędzy naprężeniami i odkształceniami betonu i stali zbrojeniowej na podstawie kryteriów materiałowych i związków obliczeniowych,
równania określające rozkład odkształceń betonu i stali zbrojeniowej na wysokości przekroju normalnego elementu na podstawie hipotezy płaskich przekrojów Bernoulli'ego oraz zasadzie równości odkształceń w stali i otaczającej warstwie betonu.
Model ten opiera się na zależności między odkształceniami i naprężeniami w betonie strefy ściskanej na podstawie wykresu paraboliczno-prostokątnego oraz definiuje obliczeniową, bilinearna zależność między naprężeniami i odkształceniami w przekroju zbrojenia.
Pokazana na rys. 1a obliczeniowa funkcja naprężeń jest funkcją złożoną o postaci:
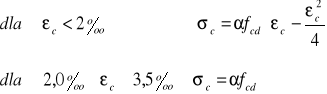
gdzie: fcd - obliczeniowa wytrzymałością betonu na ściskanie a α - współczynnik korekcyjny wyrażający wpływ uplastycznienia betonu w strefie ściskanej i niekorzystnego sposobu przyłożenia obciążeń (przy zginaniu i ściskaniu elementów z betonu zwykłego przyjmuje się α = 0,85).
Zgodnie z wyżej podanymi założeniami stan graniczny nośności przekroju zostanie osiągnięty, gdy spełniony będzie przynajmniej jeden z poniższych warunków odkształceń:
odkształcenia εs w zbrojeniu rozciąganym osiągną wartość graniczną równa 10,0 %o ,
odkształcenia εc w skrajnym włóknie ściskanym betonu osiągną wartość 3,5%o ,
odkształcenia we włóknie ściskanym betonu w odległości 3/7 h od krawędzi ( h jest wysokością przekroju ) osiągną wartość 2%o .
Ponieważ odkształcenia włókien w przekrojach żelbetowych, zgodnie z założeniem o płaskich przekrojach są proporcjonalne do odległości tych włókien od osi obojętnej, związek obliczeniowy pozwala określić kształt wykresu naprężeń w strefie ściskanej betonu zginanego elementu żelbetowego. Odkształcenia włókien betonu w strefie ściskanej są jednocześnie związane z wydłużeniem ( skróceniem ) włókien zbrojenia. Wykres naprężeń na wysokości strefy ściskanej betonu w strefie granicznym nośności, w zależności od stanu odkształcenia zbrojenia będzie przyjmował różne kształty. Powyższe warunki prowadzą do całej rodziny funkcji opisujących możliwe zachowanie się obliczanego przekroju. Przykładowe sytuacje obliczeniowe pokazano na rysunku 2.
W metodzie uproszczonej, która jest dopuszczona zarówno przez Eurokod 2 jak i normę PN-99 podtrzymuje się wymienione wyżej założenia podstawowe, w celu uproszczenia obliczeń przyjmuje się prostokątny lecz zmodyfikowany wykres naprężeń na wysokości strefy ściskanej.
Zakresy odkształceniowe w analizie przekrojów zginanych.
W celu usystematyzowania postępowania opartego o podane wyżej kryteria nośności granicznej przekroju żelbetonowego proponuje się rozpatrzenie przekrojów zginanych w kilku różnych zakresach stanu odkształceniowo-naprężeniowego w betonie i stali Zbrojeniowej. Zakresy te podano w tablicy 1.
Omówione w tablicy przedziały odkształceń w zakresach obliczeniowych 1a, 1b , oraz 2 wskazują, że naprężenia w zbrojeniu rozciąganym osiągają wytrzymałość obliczeniową fyd co oznacza, że mechanizm zniszczenia przekroju w stanie granicznym nośności prowadzi do wyczerpania nośności w przekrojach zbrojenia rozciąganego. Zakresy te są wykorzystywane do celów wymiarowania elementów zginanych i ściskanych z dużym mimośrodem. Natomiast przedział określony w zakresie obliczeniowym 3 oznacza, że naprężenia w zbrojeniu nie osiągną wytrzymałości obliczeniowej fyd . Oznacza to, że mechanizm zniszczenia przekroju następuje poprzez wyczerpanie nośności betonu w strefie ściskanej, bez uplastycznienia stali zbrojenia rozciąganego. Zakres ten nie może być podstawą do wymiarowania belek zginanych, może być natomiast wykorzystywany do wymiarowania przekrojów ściskanych z małym mimośrodem.
Z analizy płaskich przekrojów wynika, że kolejne zakresy odkształceń można uzależnić od zasięgu strefy ściskanej x w przekroju. Przedziały zasięgu strefy ściskanej w poszczególnych zakresach obliczeniowych podano na rysunku 3.
Wykresy odkształceń i naprężeń w ogólnym przypadku przekroju symetrycznego w żelbetowym elemencie podlegającym zginaniu, w zakresach obliczeniowych 1a oraz 1b pokazano na rysunku 4.
Analogiczne wykresy obowiązujące dla zakresu obliczeniowego 2 zamieszczono na rysunku 5.
Z przytoczonych wykresów naprężeń w betonie strefy ściskanej wynika, że każdy zakres charakteryzuje się innym opisem wypadkowej naprężeń w strefie ściskanej, jak również momentu granicznego przenoszonego przez przekrój zginany.
Obliczenie przekroju zginanego w każdym z wymienionych zakresów jest możliwe poprzez wykorzystanie wymienionych wcześniej warunków obliczeniowych, a konkretnie:
- warunków zgodności naprężeń i odkształceń opisanych obliczeniową funkcją σ − ε ,
- warunków równowagi sił wewnętrznych w betonie i stali zbrojeniowej.
ALGORYTM OBLICZANIA ZBROJENIA
PRZEKROJU PROSTOKĄTNEGO POJEDYŃCZO ZBROJONEGO
METODĄ UPROSZCZONĄ
Dane:
przekrój: b x h
moment obliczeniowy Msd
klasa betonu ( np. B20 )
klasa stali ( np. A3 )
klasa środowiska
Tok postępowania:
Ustalenie wysokości użytecznej przekroju.
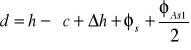
W przypadku zbrojenia w jednym rzędzie, natomiast gdy zbrojenie układane jest w dwóch lub trzech rzędach należy wyliczyć odległość środka ciężkości zbrojenia od pręta strzemiona ( w przypadku stosowania tego wzoru ).
Analityczne wyznaczenie zasięgu ξeff efektywnej strefy ściskania:
przekształcając równanie równowagi momentów:
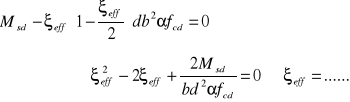
lub wykorzystując tablice obliczyć współczynnik wejsciwy do tablic μeff
![]()
Wyznaczenie pola przekroju zbrojenia rozciąganego.
z wykorzystaniem warunku równowagi sił wewnętrznych stosując współczynnik ξeff:
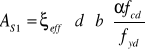
z wykorzystaniem warunku równowagi momentów stosując współczynnik ζeff:
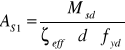
UWAGA! Jeśli wartość wejściowa do tablic lokuje zasięg strefy ściskanej ξeff poza przedziałem wartości ξlim określonych w tablicy, oznacza to przypadek przekroju wymagającego dozbrojenia w strefie ściskanej.
ALGORYTM OBLICZANIA ZBROJENIA
PRZEKROJU PROSTOKĄTNEGO POJEDYŃCZO ZBROJONEGO
METODĄ UPROSZCZONĄ
Dane:
przekrój: b x h
moment obliczeniowy Msd
klasa betonu ( np. B20 )
klasa stali ( np. A3 )
klasa środowiska
Tok postępowania:
Ustalenie wysokości użytecznej przekroju.
Analityczne wyznaczenie zasięgu ξeff efektywnej strefy ściskania:
przekształcając równanie równowagi momentów:
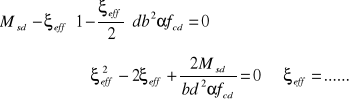
lub wykorzystując tablice obliczyć współczynnik wejściowy do tablic μeff
![]()
3) Wyznaczenie pola przekroju zbrojenia rozciąganego.
z wykorzystaniem warunku równowagi sił wewnętrznych stosując współczynnik ξeff:
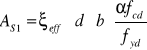
z wykorzystaniem warunku równowagi momentów stosując współczynnik ζeff:
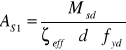
UWAGA! Jeśli wartość wejściowa do tablic lokuje zasięg strefy ściskanej ξeff poza przedziałem wartości ξlim określonych w tablicy, oznacza to przypadek przekroju wymagającego dozbrojenia w strefie ściskanej.
ALGORYTM OKREŚLANIA NOŚNOŚCI
PRZEKROJU PROSTOKĄTNEGO POJEDYŃCZO ZBROJONEGO
METODĄ UPROSZCZONĄ
Dane:
wymiary przekroju: b x h
przekrój zbrojenia: As1
klasę betonu
klasę stali
klasę środowiska
Tok postępowania:
Ustalenie wysokości użytkowej d.
Wyznaczenie wartości ξeff na podstawie równia sumy rzutów sił wypadkowych w SGN:
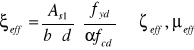
Wyznaczenie analityczne nośności granicznej przekroju wykorzystując:
warunek równowagi momentów względem osi zbrojenia As1:
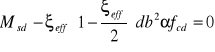
wykorzystując tablice pomocnicze:
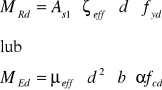
Wyszukiwarka
Podobne podstrony:
SX026 Przykład Sprawdzenie stanów granicznych nośności i użytkowalności zginanego elementu z kształt
Wytrzymałość materiałów, Zginanie proste -wyznaczanie granicznej nośności belki zginanej, Wy?sza Szk
A Biegus Cz 6 Elementy zginane 2013 11 27
Eurokod 2-algorytm obliczania zbrojenia dla elementów zginanych, przekrój podwójnie zbrojony
Ochrona przeciwogniowa elementów konstrukcji w technologii szkieletu drewnianego
Eurokod 2 algorytm obliczania zbrojenia dla elementów zginanych przekrój podwójnie zbrojony
Ochrona przeciwogniowa elementów konstrukcji w technologii szkieletu drewnianego, Konstrukcje ciesie
Eurokod 2 algorytm obliczania zbrojenia dla elementów zginanych przekrój pojedynczo zbrojony
Seminarium - referaty, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I sto
Ochrona przeciwogniowa elementów konstrukcji w technologii szkieletu drewnianego
Eurokod 2 algorytm obliczania zbrojenia dla elementów zginanych tabele
Algorytm wymiarowania zbrojenia strzemionami prostopadłymi w elemencie zginanym z udziałem sił poprz
Wielokondygnacyjne konstrukcje stalowe Opis kalkulatora do obliczania nośności elementów konstrukcyj
więcej podobnych podstron