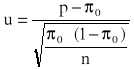TESTOWANIE HIPOTEZY O WSKAŹNIKU STRUKTURY

Niech rozważana zbiorowość ma rozkład dwupunktowy z parametrem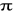
oznaczającym prawdopodobieństwo, że badana zmienna przyjmie wyróżnioną wartość. Wartość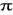
nazywamy wskaźnikiem struktury (frakcją lub procentem). Wówczas możliwa jest weryfikacja następujących hipotez na podstawie:

1. testu jednostronnego (lewostronny)

1. Postawienie hipotezy zerowej i alternatywnej:

,
,

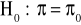
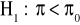
gdzie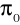
jest hipotetyczną wartością prawdopodobieństwa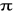
.

2. Wybranie testu statystycznego o postaci

,

gdzie

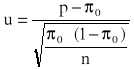
u - przy prawdziwości hipotezy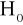
, jest statystyką o rozkładzie normalnym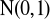
,

m - liczba jednostek o wyróżnionej wartości cechy,

n - liczba wszystkich jednostek analizowanej zbiorowości,

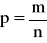
- empiryczna wartość prawdopodobieństwa.

Iloraz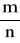
określa udział jednostek o wyróżnionej wartości cechy w ogólnej liczbie jednostek, zatem jest wskaźnikiem struktury, który możemy traktować jako empiryczne prawdopodobieństwo przyjęcia przez daną cechę wyróżnionej wartości.

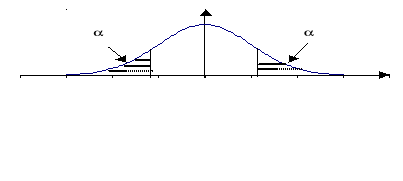
3. Wyznaczenie wartości krytycznej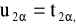
   na podstawie tablic statystycznych dla rozkładu t-Studenta i nieskończonej liczby stopni swobody oraz zbioru krytycznego (obszar zakreskowany na rysunku),

Weryfikacja hipotezy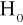
odbywa się następująco:

• wartość statystyki obliczonej na podstawie próby losowej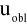
  leży poza obszarem krytycznym:

Nie ma podstaw do odrzucenia hipotezy zerowej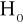
mówiącej, że wskaźnik struktury dla zbiorowości jest równy wartości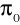
.

• wartość statystyki obliczonej leży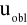
  w obszarze krytycznym

Odrzucamy hipotezę zerową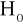
na korzyść hipotezy alternatywnej mówiącej, że wskaźnik struktury dla zbiorowości jest mniejszy od wartości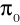
.

W kolejnych przypadkach zostaną wyróżnione tylko te elementy, które różnią się od wymienionych w podejściu I.

2. testu dwustronnego

,
,

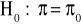
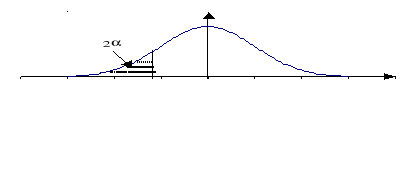
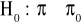
Wartość statystyki obliczonej leży w obszarze krytycznym:

Odrzucamy hipotezę zerową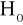
na korzyść hipotezy alternatywnej mówiącej, że wskaźnik struktury dla zbiorowości jest różny od wartości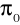
.

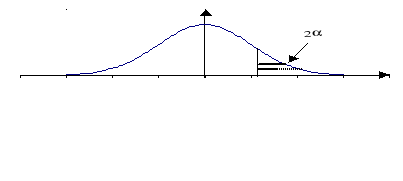
3. test jednostronnego (prawostronny)

,
,

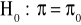
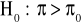
Wartość statystyki obliczonej leży w obszarze krytycznym:

Odrzucamy hipotezę zerową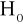
na korzyść hipotezy alternatywnej mówiącej, że wskaźnik struktury dla zbiorowości jest większy od wartości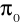
.

Przedział ufności dla wskaźnika struktury

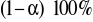
przedział ufności dla wskaźnika struktury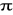
jest postaci

.

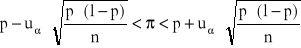
Interpretacja przedziału ufności:

Z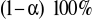
ufnością rzeczywisty wskaźnik struktury zbiorowości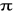
pokryty jest przedziałem o końcach - lewym L i prawym P.