Opracowanie wyników

Sporządzamy krzywą cechowania osi x programu obsługi spektrometru, wykorzystując pomiar długości fali Hg(Ar). Wykreślamy zależność długości fali rzeczywistej od podawanej przez program. Wybieramy długości fali najbardziej intensywnych linii Hg(Ar) z zakresu promieniowania widzialnego i porównujemy je z danymi podanymi w tabeli. Dane pochodzą z tablic American Physics Handbook.

Wartości w poniższej tabelce przedstawiają długości fal λ w najbardziej charakterystycznych i widocznych maksimach. Jednostką miary są nanometry [nm].

Wartości tablicowe				Wartości średnie
Uśrednianie:	15	20	25
Czas ekspozycji [ms]:	2000	3000	4000
435,84	434	434	434	434
546,07	547	547	547	547
696,54	697	697	697	697
751,47	753	753	753	753
763,51	765	766	766	766

Pomiar wykonywany był dla fal o długościach od 380 - 780 nm, gdyż taki był zakres spektrometru światłowodowego użytego w tym doświadczeniu. Jego rozdzielczość wynosiła 3 nm, zatem zakładamy, że bezwzględny błąd pomiaru długości λ ma wartość:

Δλ = 3 nm

Przeprowadzając doświadczenie nie odnotowaliśmy żadnych wskazań spektrometru w okolicach długości 488 i 615 nm, choć dane tablicowe wyraźnie wskazywały na obecność linii widmowych o tych długościach. Przyczyną zaistniałego błędu pomiarowego mogło być zanieczyszczenie próbek Hg(Ar) oraz wyeksploatowanie sprzętu pomiarowego. Mogła być to także przyczyna nieoczekiwanego pojawienia się dość wyraźnego maksima w okolicach długości 707 nm.

Wykorzystujemy metodę najmniejszych kwadratów polegająca na minimalizacji sumy kwadratów odchyłek miedzy punktami doświadczalnymi a dopasowaną krzywą. Długości fal otrzymane dla widma wodoru korygujemy korzystając z zależności:

Wartości tablicowe				Wartości średnie	Skorygowane długości fal	1 / długość fali (nm^-1)	n	1 / n^2
Uśrednianie:	15	20	25
Czas ekspozycji [ms]:	2000	3000	4000
434,05	433	432	433	433	434,31	0,0023025	5	0,0400
486,13	487	487	487	487	487,78	0,0020501	4	0,0625
656,28	658	658	658	658	657,13	0,0015218	3	0,1111

∆λ = 2,97 nm

„n” jest główną liczbą kwantową, która numeruje kolejne poziomy energetyczne o określonym momencie pędu danym orbitalną liczbą kwantową l, przy czym n = l+1, l+2, l+3, itd.

Wyznaczamy błąd obliczenia odwrotności długości fali korzystając z prawa przenoszenia błędów:

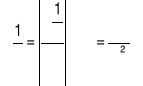
Skorygowane długości fal	1 / długość fali (nm^-1)	∆ (1 / λ) (nm^-1)	n	1 / n^2
434,31	0,0023025	0,0000157	5	0,0400
487,78	0,0020501	0,0000125	4	0,0625
657,13	0,0015218	0,0000069	3	0,1111

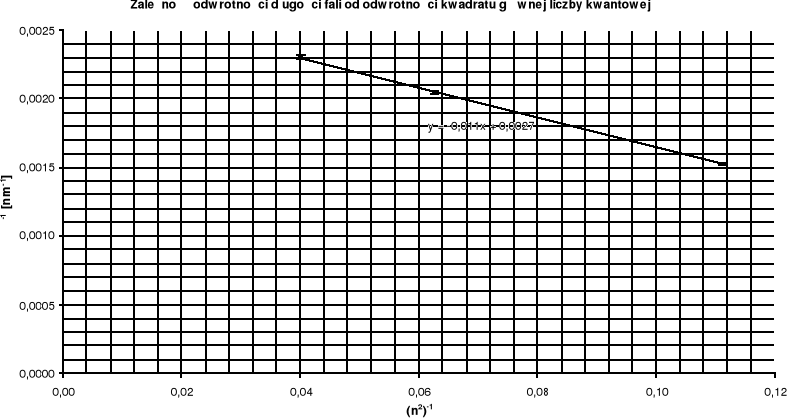
Przez punkty prowadzimy prostą wyznaczoną metodą najmniejszych kwadratów. Powinna ona spełniać poniższe równanie:

,

gdzie R jest stałą Rydberga wyznaczaną w doświadczeniu.

Współczynnik kierunkowy „a” i odcięta „b” dla tej prostej wynoszą odpowiednio:

a = -10961267,65 · 10^-9

b = 2738607,04 · 10^-9

Jak widać ze wzoru przytoczonego powyżej, wyznaczony współczynnik „-a” jest poszukiwaną stałą Rydberga i wynosi:

R = 10961267,65 [m^-1]

Korzystając ze wzoru na średni błąd kwadratowy obliczamy niepewność otrzymanej wartości:

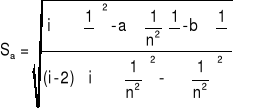
S_a = 83043,5 m^-1

Energię jonizacji obliczamy przekształcając równanie:

,

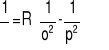
gdzie „o” i „p” są odpowiednio orbitalmi z którego i na który zostaje przeniesiony elektron. Ponieważ energia jonizacji jest energią, jaką musi zaabsorbować atom, aby elektron z powłoki, gdzie ma największą energię został przeniesiony do nieskończoności, to za „o” podstawiamy 1 a za p = ∞.

Korzystamy z zależności
,
i otrzymujemy
czyli
, gdzie E jest wyznaczaną energią jonizacji, R - wyznaczoną w doświadczeniu stałą Rydberga,
h = 6,62491⋅10^-34 J⋅s - stałą Plancka, a c = 299 860 ± 80 km/s - prędkością światła.

Znaczący wpływ na wyniki i niedokładność naszych pomiarów miała niska rozdzielczość spektrometru światłowodowego, która wynosiła zaledwie 3 nm, co w porównaniu z wartościami podawanymi w tablicach - z dokładnością do dwóch miejsc po przecinku, wydaje się dużym zaokrągleniem. Ponieważ pomiary dawały wyniki z dokładnością do 10^-3, a jak już wspomniałem, rozdzielczość spektrometru światłowodowego wynosiła 3 nm wyniki zaokrągliliśmy do jedności. Przy przeliczaniu odwrotności długości fali i n² zachowaliśmy jak największą dokładność, gdyż otrzymywane wyniki były ułamkami bliskimi zeru, a to mogło spowodować poważny błąd w dalszych obliczeniach. Otrzymywane wyniki tylko nieznacznie odbiegają od danych tablicowych, a błąd rzędu 10⁴, gdzie wartość stałej Rydberga R jest rzędu 10⁷, przy tak mało dokładnych urządzeniach pomiarowych wydaje się zrozumiała.

---