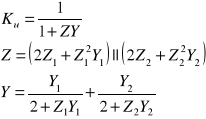Politechnika Częstochowska

Wydział Elektryczny

Katedra Elektrotechniki

Zakład Elektrotechniki

Laboratorium Elektrotechniki Teoretycznej

Badanie czwórników

Częstochowa 2004

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z parametrami czwórników oraz wyznaczenie transmitancji napięciowo-napięciowej wybranych czwórników w zakresie częstotliwości akustycznych.

2. Wiadomości podstawowe

2.1. Czwórniki

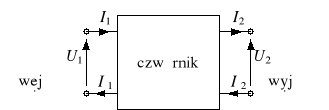
Czwórnik - element czterozaciskowy z wyróżnioną parą zacisków wejściowych i wyjściowych, spełniający warunki równości prądów I1 = I′1 oraz I2 = I′2 (rys. 1). Przyjmuje się, że prąd I1 jest skierowany do czwórnika, a prąd I2 - od czwórnika (w literaturze spotyka się też obydwa prądy zastrzałkowane do czwórnika).

Rys. 1. Czwórnik

Zależności pomiędzy dwiema wielkości wejściowymi U₁ i I₁ oraz wyjściowymi U₂ i I₂ mogą być przedstawione na sześć różnych sposobów:

• jako równania łańcuchowe, gdy wyrażają U₁ i I₁ poprzez U₂ i I₂,

• jako równania łańcuchowe odwrotne, gdy wyrażają U₂ i I₂ poprzez U₁ i I₁,

• jako równania impedancyjne, gdy wyrażają U₁ i U₂ poprzez I₁ i I₂,

• jako równania admitancyjne, gdy wyrażają I₁ i I₂ poprzez U₁ i U₂,

• jako równania hybrydowe, gdy wyrażają U₁ i I₂ poprzez I₁ i U₂,

• jako równania hybrydowe odwrotne, gdy wyrażają I₁ i U₂ poprzez U₁ i I₂.

Zależności te wyraża się zwykle poprzez tzw. macierze czwórnika. Zastosowanie tych zależności zależy od rodzaju zagadnienia.

2.2. Macierz łańcuchowa czwórnika

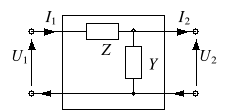
W instrukcji ograniczymy się do podania wzorów dotyczących równań łańcuchowych czwórnika, tj.

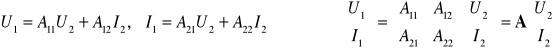
Macierz A nosi nazwę macierzy łańcuchowej. Jej poszczególne elementy określa się następująco:

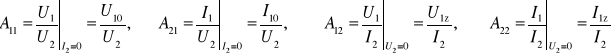
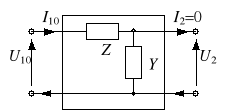
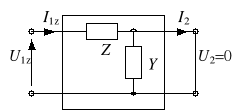
Wynika stąd, że współczynniki te można łatwo wyznaczyć z pomiarów w stanie jałowym (I₂ = 0) oraz w stanie zwarcia (U₂ = 0). Rozważmy przykładowo czwórnik
(rys. 2).

a)	b)	c)

Rys. 2. Czwórnik typu
(a), stan jałowy (b) i stan zwarcia (c)

Dla stanu jałowego (I₂ = 0) otrzymujemy (rys. 2b)

skąd

Z kolei dla stanu zwarcia otrzymujemy (rys. 2c)

skąd

Zatem macierz łańcuchowa czwórnika typu
wynosi

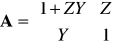
2.3. Transmitancja napięciowo-napięciowa

Transmitancję napięciowo-napięciową czwórnika w stanie jałowym określamy jako

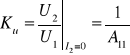
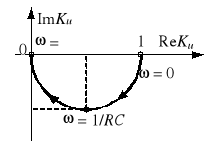
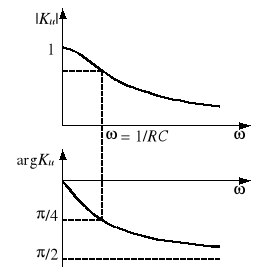
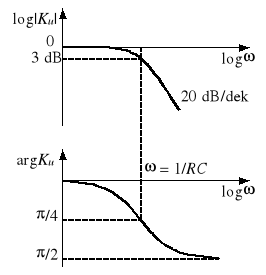
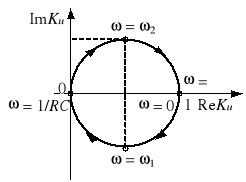
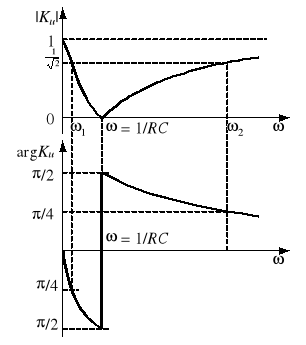
Jeżeli napięcie wejściowe jest sinusoidalnie zmienne, to również napięcie wyjściowe jest sinusoidalnie zmienne. Wtedy U₁ i U₂ są zespolonymi wartościami skutecznymi odpowiednich napięć, a transmitancja K_u jest liczbą zespoloną, zależną od pulsacji . Liczbę tę można przedstawić graficznie na płaszczyźnie zespolonej w postaci punktu. Gdy  zmienia się od 0 do ∞, punkty te układają się w krzywą zwaną hodografem lub charakterystykę amplitudowo-fazową transmitancji K_u. Czasami wygodniej jest przedstawić oddzielnie zależność |K_u| od  (ch-ka amplitudowa) oraz argK_u od  (ch-ka fazowa). Często używa się zależności 20log|K_u| od  - jest to tzw. amplitudowa charakterystyka logarytmiczna modułu transmitancji. Bardzo często oś pulsacji skaluje się logarytmicznie.

Poniżej zestawiono transmitancje K_u wybranych typów czwórników, a na rysunku 3 pokazano charakterystyki częstotliwościowe czwórnika typu
dla Z = R i Y = jC.

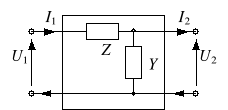
Czwórnik typu
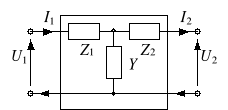
Czwórnik typu T

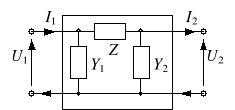
Czwórnik typu 
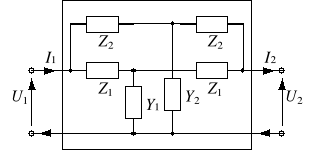
Symetryczny czwórnik typu TT

a)	b)	c)

Rys. 3. Charakterystyki częstotliwościowe K_u() czwórnika
dla Z = R, Y = jC:
a) hodograf, b) ch-ka amplitudowa i fazowa, c) 20log|K_u| i argK_u z logarytmiczną skalą osi 

2.4. Parametry falowe czwórnika symetrycznego

Czwórnik nazywamy odwracalnym, gdy stosuje się do niego twierdzenie o wzajemności. Dla czwórnika odwracalnego detA = 1.

Czwórnik nazywamy symetrycznym, gdy po zamianie miejscami wejścia i wyjścia rozkład prądów i napięć w obwodzie poza czwórnikiem nie zmieni się. Dla czwórnika symetrycznego macierz A^-1 = A. Oznacza to, że czwórnik symetryczny jest odwracalny, a ponadto A₁₁ = A₂₂. Wobec tego czwórnik symetryczny określony jest jedynie dwoma niezależnymi parametrami, gdyż mamy dodatkowo zależności detA = 1 oraz A₁₁ = A₂₂.

Impedancją charakterystyczną (zwaną też falową) czwórnika symetrycznego nazywamy taką impedancję Z_c, która dołączona do wyjścia czwórnika powoduje, że impedancja wejściowa czwórnika jest także równa Z_c. Można pokazać, że jest ona równa

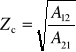
Współczynnikiem przenoszenia czwórnika symetrycznego nazywamy taką liczbę γ, że gdy czwórnik jest obciążony impedancją falową, to

Można pokazać, że

Współczynnikiem tłumienia  nazywamy część rzeczywistą współczynnika przenoszenia

Współczynnikiem fazowym  nazywam część urojoną współczynnika przenoszenia

Można też pokazać, że

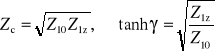
gdzie Z₁₀ - impedancja wejściowa w stanie jałowym, Z_1z - impedancja wejściowa w stanie zwarcia. Pozwala to wyznaczyć parametry Z_c i γ, a tym samym macierz A, na podstawie pomiarów impedancji w stanie zwarcia i w stanie jałowym. Macierz A jest równa

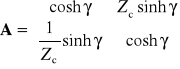
2.5. Filtry LC

Filtr - urządzenie przepuszczające bez tłumienia (lub ze stosunkowo małym tłumieniem) sygnały w określonym paśmie częstotliwości, a tłumiące sygnały poza tym pasmem. W teorii obwodów rozróżnia się wiele rodzajów filtrów, m.in. filtry LC, filtry RC oraz filtry aktywne.

W filtrach LC pasmo przepuszczania filtru definiuje się jako zakres częstotliwości (lub pulsacji), dla których  = 0. Ponieważ

to dla  = 0 otrzymujemy

skąd wynika, że w paśmie przepuszczania

Wobec tego równania

wyznaczają granice pasma przepustowego. Jeśli obciążenie jest falowe (Z₂ = Z_c) to w paśmie przepuszczania napięcie wyjściowe U₂ równa się

a więc jest równe co do modułu napięciu U₁, lecz opóźnia się o kąt .

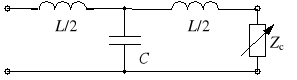
Dla filtru LC typu T (Z₁ = Z₂ = jL/2, Y = jC) mamy

skąd wynika, że pasmo przepuszczania znajduje się w zakresie pulsacji (wynikającym ze wzoru |A₁₁| ≤ 1)

Jest to więc filtr dolnoprzepustowy. Można pokazać, że

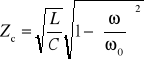
Dla pulsacji  < ₀ ma ona charakter rezystancyjny, a dla  > ₀ - indukcyjny.

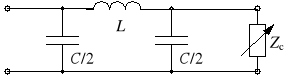
Analogiczne zależności otrzymuje się dla filtru LC typu  (Y₁ = Y₂ = jC/2, Z = jL).

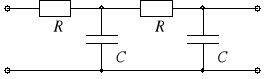
2.6. Filtr pasmowo zaporowy RC typu TT

Przyjmując w czwórniku TT

i oznaczając  = RC, otrzymuje się

Charakterystyki czwórnika pokazano na rysunku 4.

a)	b)

Rys. 4. Charakterystyki częstotliwościowe K_u() czwórnika TT dla Z₁= R, Y₁ = j2C, Z₂ = 1/jC, Y₂ = 2/R

Z rysunku 4 wynika, że rozpatrywany czwórnik jest filtrem pasmowozaporowym, przy czym pasmo zaporowe wyznacza zakres ₁÷₂. W tym paśmie |K_u| ≤ 1/√2, tzn. 20log|K_u| ≤ 3 dB. Pulsacje graniczne są równe

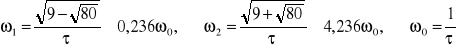
2.7. Układy różniczkujące i całkujące RC

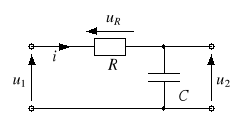
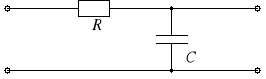
Rozważmy czwórnik typu
pokazany na rysunku 5a. Wartość chwilowa napięcia u₂ w stanie jałowym wynosi

Ponadto u₁ = u_R + u₂. Dla u_R >> u₂ mamy więc w przybliżeniu u₁ ≈ u_R, czyli

Jest to zatem układ całkujący. Należy jednak zwrócić uwagę, że warunek u_R >> u₂ nie zawsze jest spełniony. W odniesieniu do napięć sinusoidalnie zmiennych w czasie warunek ten będzie spełniony, jeśli R >> 1/C, czyli dla  >> 1/RC.

a)	b)

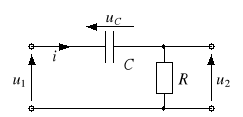
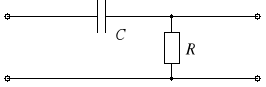
Rys. 5. Układ całkujący RC (a) i różniczkujący (b)

Podobnie w czwórniku
pokazanym na rysunku 5b mamy

Ponadto u₁ = u_C + u₂. Dla u_C >> u₂ mamy więc w przybliżeniu u₁ ≈ u_C, czyli

Jest to zatem układ różniczkujący. Należy jednak zwrócić uwagę, że warunek u_C >> u₂ nie zawsze jest spełniony. W odniesieniu do napięć sinusoidalnie zmiennych w czasie warunek ten będzie spełniony, jeśli 1/C >> R, czyli dla  << 1/RC.

3. Przebieg ćwiczenia

Ćwiczenie może być wykonywane na dwóch różnych stanowiskach.

3.1. Stanowisko modelowe 1

Stanowisko składa się z płytki, na której znajdują się wybrane czwórniki. Schemat płytki pokazano na rysunku 6. Wartości parametrów elementów znajdujących się na płytce wynoszą:

R = 1 k,

L = 0,24 H,

C = 220 nF.

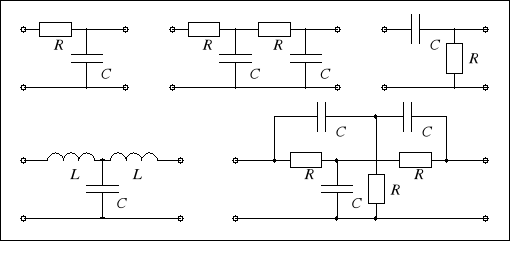
Rys. 6. Widok panelu płytki do badania czwórników

Na wejście badanego czwórnika podłączamy generator napięcia sinusoidalnego, na wyjście woltomierz cyfrowy (woltomierz V₁ znajduje się w generatorze) - rys. 7. Oscyloskop służy do pomiaru przesunięcia fazowego. W tym celu do kanału A oscyloskopu podajemy napięcie wejściowe, a do kanału B - wyjściowe.

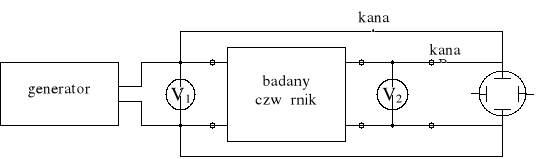
Rys. 7. Schemat układu pomiarowego

3.2. Stanowisko modelowe 2

Stanowisko modelowe zawiera:

• generator napięcia sinusoidalnego,

• cztery zestawy elementów R, L i C,

• mierniki napięcia wejściowego i wyjściowego,

• miernik przesunięcia fazowego między napięciem wyjściowym a wejściowym.

Generator ma możliwość regulacji częstotliwości w zakresie od 160 Hz do 32 kHz oraz amplitudy od 0 do 1500 mV. Każdy z elementów R, L, C w każdym z czterech zestawów elementów może zostać nastawiony na jedną z trzech wartości (tabela 1). Wyprowadzone zaciski pozwalają na zbudowanie szerokiej gamy czwórników. Ponadto istnieje możliwość podłączenia oscyloskopu na wejście i wyjście układu. Widok panelu czołowego stanowiska laboratoryjnego przedstawia rysunek 8.

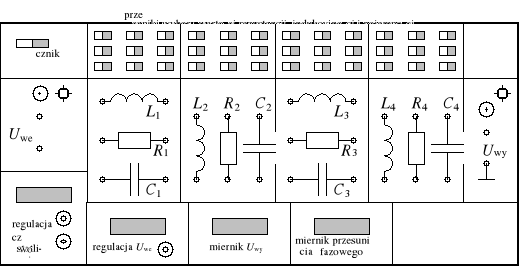
Rys. 8. Widok panelu czołowego stanowiska laboratoryjnego

Tabela 1

Lp.	R, 	L, mH	C, F
1	47	2,2	8,2
2	22	1,2	4,7
3	10	0,47	2,2

3.3. Badanie układu całkującego i różniczkującego typu RC

• Zestawić układ całkujący typu RC (rys. 9) (UWAGA: w przypadku zastosowania stanowiska 2 należy użyć rezystora dekadowego),

WERSJA 1 R = 1 k C = 220 F

WERSJA 2 R = 10 k C = 2.2 F

Rys. 9.

• Zmieniając częstotliwość w granicach od 200 Hz do 2 kHz i utrzymując napięcie U₁ = 1 V, zmierzyć napięcie U₂ oraz przesunięcie fazowe (tabela 2),

• Pomiary powtórzyć dla układu różniczkującego RC (rys. 10).

WERSJA 1 R = 1 k C = 220 F

WERSJA 2 R = 10 k C = 2.2 F

Rys. 10.

Tabela 2

f, Hz
U2, V
argKu, °
|Ku|

3.4. Badanie czwórnika RC typu podwójne

• Zestawić układ całkujący typu RC (rys. 11) (UWAGA: w przypadku zastosowania stanowiska 2 należy użyć rezystorów dekadowych),

WERSJA 1 R = 1 k C = 220 F

WERSJA 2 R = 10 k C = 2.2 F

Rys. 11.

• Pomiary jak w punkcie 3.3.

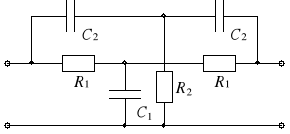
3.5. Wyznaczanie transmitancji K_u czwórnika typu TT

• Zestawić czwórnik pokazany na rysunku 12,

WERSJA 1 R1 = 1 k R2 = 1 k C1 = 220 F C2 = 220 F

WERSJA 2 R1 = 47  R2 = 22  C1 = 8,2 F C2 = 4,7 F

WERSJA 3 R1 = 250  R2 = 125  C1 = 2 F C2 = 1 F

Rys. 12.

• Zmieniając częstotliwość od 200 Hz do 2 kHz i utrzymując U₁ = 1 V, zapisywać wyniki w tabeli 2 (uchwycić minimum napięcia wyjściowego).

3.6. Badanie filtrów dolnoprzepustowych typu T i 

• Zestawić filtr LC typu T pokazany na rysunku 13,

WERSJA 1 L/2 = 0,24 H C = 220 F

WERSJA 2 L/2 = 0,47 mH C = 2.2 F

WERSJA 3 L/2 = 10 mH C = 15 nF

Rys. 13.

• Określić częstotliwość graniczną f₀:

• Jako obciążenie podłączyć opornik dekadowy, którego wartość należy ustawiać po każdej zmianie częstotliwości na wartość równą impedancji charakterystycznej Z_c:

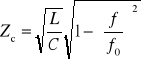
• Zmieniając częstotliwość od 200 Hz do f₀ i utrzymując U₁ =1 V oraz Z₂ = Z_c, mierzyć napięcie wyjściowe oraz przesunięcie fazowe (tabela 3),

• Pomiary powtórzyć dla filtra LC typu  (rys. 14), przy czym wtedy

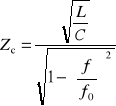
WERSJA 1 L = 0,24 H C/2 = 220 F

WERSJA 2 L = 0,47 mH C/2 = 2.2 F

WERSJA 3 L = 10 mH C/2 = 15 nF

Rys. 14.

Tabela 3

f, Hz
Zc, 
U2, V
argKu, °
|Ku|

4. Opracowanie sprawozdania

1. Cel ćwiczenia.

2. Schematy pomiarowe i tabele wyników.

3. Parametry i dane znamionowe zastosowanych przyrządów.

4. Przykłady obliczeń poszczególnych wartości podanych w tabelach.

5. Dla każdego badanego czwórnika wyznaczyć teoretyczną ch-kę K_u(). Na podstawie otrzymanych zależności wykreślić |K_u()| argK_u() oraz hodografy K_u() dla wszystkich badanych czwórników i nanieść punkty otrzymane z pomiarów; porównać wartości teoretyczne i zmierzone.

6. Wnioski.

5. Pytania sprawdzające

1. Co to jest czwórnik?

2. Podać równania łańcuchowe czwórnika.

3. Podać inne rodzaje równań (impedancyjne, admitancyjne itd.).

4. Jak doświadczalnie można wyznaczyć macierz łańcuchową czwórnika?

5. Co to jest transmitancja napięciowo-napięciowa?

6. Wymienić i omówić charakterystyki częstotliwościowe czwórnika na przykładzie transmitancji napięciowo-napięciowej.

7. Co to jest czwórnik odwracalny, a co symetryczny?

8. Ile niezależnych wielkości określa czwórnik symetryczny?

9. Omówić parametry falowe czwórnika symetrycznego.

10. Jak z pomiarów można wyznaczyć parametry falowe czwórnika symetrycznego?

11. Co to jest filtr?

12. Co to jest pasmo przenoszenia filtru?

13. Jak na podstawie macierzy łańcuchowej można wyznaczyć pasmo przenoszenia filtru LC?

14. Wyprowadzić wzór na K_u dla filtru TT.

15. Omówić działanie układu różniczkującego RC.

16. Omówić działanie układu całkującego RC.

Literatura

[1] Bolkowski S.: Elektrotechnika teoretyczna, tom I - teoria obwodów elektrycznych, WNT, W-wa 1986, ss. 357-419.

[2] Cholewicki T.: Elektrotechnika teoretyczna, tom I, WNT, W-wa 1967, ss. 699-805.

[3] Krakowski M.: Elektrotechnika teoretyczna, tom I - obwody liniowe i nieliniowe, PWN, W-wa 1991, ss. 350-398.

[4] Kurdziel R.: Podstawy elektrotechniki, WNT, W-wa 1972, ss. 746-778.

[5] Rajski Cz.: Teoria obwodów, tom 1, WNT, W-wa 1971, ss. 233-286.

Dodatek

Dla czwórnika symetrycznego typu TT, w którym

otrzymuje się

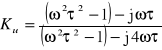
przy czym  = RC.

Badanie czwórników

10

Politechnika Częstochowska, Wydział Elektryczny, Katedra Elektrotechniki

---