I. Wstęp teoretyczny.

Rozkład Poissona.

Emisja cząstek z preparatu radioaktywnego nie następuje w równych odstępach czasu, lecz podlega fluktuacjom statystycznym. Przeciętne odchylenie względne pojedynczego pomiaru od wartości średniej , czyli fluktuacja statystyczna jest tym większe , im mniejsza jest aktywność preparatu radioaktywnego.

Wyniki pomiarów w ustalonym przedziale czasu t , to znaczy liczby zliczeń zarejestrowane przez układ liczący w tym przedziale t , podlegają rozkładowi Poissona opisywanemu funkcją analityczną w postaci

gdzie: P(m) - prawdopodobieństwo, że w czasie t układ zarejestruje liczbę m. Impulsów

- średnia liczba impulsów obliczona na podstawie bardzo dużej ilości rejestracji, w takim samym czasie t.

Średni rzut wartości doświadczalnych x względem wartości rzeczywistej x₀ scharakteryzowany jest poprzez wielkość zwaną wariacją lub dyspersją zdefiniowaną wzorem

gdzie: n - ilość pomiarów.

Powszechnie przyjętą miarą dokładności pomiarów jest tzw. odchylenie standardowe (średni błąd kwadratowy) , które jest równe pierwiastkowi kwadratowemu z wariancji (dyspersji).

Odchylenie standardowe pojedynczego wyniku w serii pomiarowej spełniającej prawo rozkładu Poissona , zwane również niekiedy standardowym odchyleniem statystycznym jest równe pierwiastkowi kwadratowemu z wartości średniej.

gdzie: m. - średnia liczba zliczeń.

Względne odchylenie standardowe (średni „błąd” kwadratowy względny) pojedynczego wyniku jest w tym przypadku równy

Rozkład normalny Gaussa.

Dla preparatu o dużej aktywności dominują duże liczby zliczeń m i duża jest również wartość średnia , a rozkład Poissona można z dobrym przybliżeniem zastąpić rozkładem Gaussa.

Rozkład Gaussa jest rozkładem ciągłym i symetrycznym opisanym wzorem

gdzie: - tzw. Gęstość prawdopodobieństwa tego , iż wartość odchylenia znajduje się w przedziale x i x+dx.

Statystyczna czystość pomiarów.

Oprócz odchylenia statystycznego pomiar może zawierać jeszcze błędy systematyczne.

Jeżeli wpływ błędów systematycznych jest mały w porównaniu z rozrzutem statystycznym pomiarów , to pomiary uważane są za „statystycznie czyste”. Jeżeli błędy systematyczne są na tyle duże , że uzyskany na podstawie przeprowadzonej serii pomiarów różni się zauważalnie od rozkładu normalnego Gaussa , to pomiary nie są „statystycznie czyste”.

Względne odchylenie standardowe odchylenia standardowego wielkości podlegającej rozkładowi normalnemu Gaussa (błąd średniego błędu kwadratowego) w przypadku jednej serii pomiarowej wynosi:

II. Schemat pomiarowy.

Schemat blokowy aparatury pomiarowej:

E - źródło promieniowania γ (izotop kobaltu ⁶⁰Co)

D - detektor (licznik Geigera-Millera)

Z - zasilacz wysokiego napięcia

16. - przelicznik typ PT-72

3. Tabela pomiarowa.

Napięcie pracy licznika 460V						Czas pomiaru t = 40 s
Numer pom.	Ilość zliczeń	Numer klasy	Numer pom.	Ilość zliczeń	Numer klasy	Numer pom.	Ilość zliczeń	Numer klasy	Numer pom.	Ilość zliczeń	Numer klasy
i	m[imp]	p.	i	m[imp]	p.	i	m[imp]	p.	i	m[imp]	p
1	11501	3	26	11503	3	51	11679	8	76	11610	6
2	11434	2	27	11612	6	52	11688	8	77	11432	2
3	11679	8	28	11609	6	53	11621	6	78	11479	3
4	11699	8	29	11641	7	54	11627	6	79	11418	1
5	11551	4	30	11663	7	55	11477	3	80	11609	6
6	11477	3	31	11589	5	56	11473	3	81	11592	5
7	11494	3	32	11517	4	57	11595	6	82	11570	5
8	11682	8	33	11707	8	58	11493	3	83	11692	8
9	11546	4	34	11576	5	59	11601	6	84	11743	9
10	11391	1	35	11794	10	60	11542	4	85	11623	6
11	11502	3	36	11689	8	61	11455	2	86	11591	5
12	11416	1	37	11650	7	62	11482	3	87	11499	3
13	11428	1	38	11695	8	63	11498	3	88	11546	4
14	11544	4	39	11441	2	64	11530	4	89	11541	4
15	11482	3	40	11767	10	65	11596	6	90	11501	3
16	11539	4	41	11537	4	66	11500	3	91	11593	6
17	11740	9	42	11537	4	67	11646	7	92	11647	7
18	11532	4	43	11642	7	68	11615	6	93	11571	5
19	11665	7	44	11544	4	69	11493	3	94	11460	2
20	11632	6	45	11561	5	70	11516	4	95	11493	3
21	11565	5	46	11672	7	71	11549	4	96	11503	3
22	11503	3	47	11497	3	72	11594	6	97	11589	5
23	11405	1	48	11534	4	73	11542	4	98	11530	4
24	11638	7	49	11452	2	74	11516	4	99	11561	5
25	11523	4	50	11636	7	75	11565	5	100	11561	5
11564,8				11349,7				11779,8
11391				11794				= 40,3

	Zakres klasy
Numer klasy	granica dolna	granica górna	Ilość wyników w klasie	Częstość wyst. klasy	Suma częst. występow. klasy
p	md [imp]	mg [imp]	np [imp]	Cp [*]	[*]
1	11391	11431,3	5	5	5
2	11431,3	11471,6	6	6	11
3	11471,6	11511,9	20	20	31
4	11511,9	11552,2	20	20	51
5	11552,2	11592,5	12	12	63
6	11592,5	11632,8	14	14	77
7	11632,8	11673,1	10	10	87
8	11673,1	11713,4	9	9	96
9	11713,4	11753,7	2	2	98
10	11753,7	11794	2	2	100

= (m₁ + m₂ + m₃ + .... + m_n) / n = gdzie - średnia arytmetyczna

R = m _max - m _min =403[imp] gdzie R - rozstęp wyników serii

Δ _k - szerokość zakresu pojedynczej klasy  _k = ( m _max - m _min ) / 10=40,3[imp]

Zakres poszczególnych klas

p₁ = m_min ÷ (m _min + Δ _k = m_g1)

p₂ = m_g1 ÷ (m_g1 + Δ _k = m_g2)

p₁₀ = mg₉ ÷(m_g9 + Δ _k = m_max)

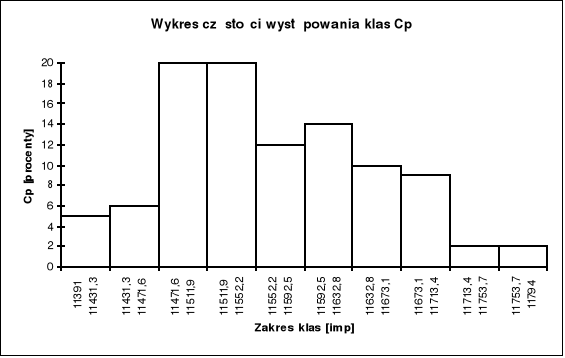
Obliczam ile pojedynczych wyników n_p mieści się w zakresie danej klasy , a następnie częstotliwość występowania klasy C_p = n_p / n , C_p (%) = %

Obliczam sumę częstości klas

∑ C_p = C₁ + C₂ + ... + C_p

Z wykresu odczytujemy odchylania d1 i d2 otrzymanej prostej doświadczalnej od teoretycznej w punktach odpowiadających 2,3% oraz 97,7%.Obliczamy wartości względne otrzymanych odchyleń.

4. WNIOSKI I UWAGI

Można zauważyć, że obliczone wartości względne odchyleń nie przekraczają 0,5%. Oznacza to że pomiary zostały wykonane ze statystyczną czystością, czyli błędy aparatury można uznać za pomijalnie małe. Ze sporządzonych wykresów zauważamy, iż te przecięły się prawie w środku ciężkości prostej teoretycznej. Prosta doświadczalna wyznaczona została poprzez odpowiednią aproksymacje naniesionych punktów przyjmując za rzędne - odpowiednie sumy częstości klas , za odcięte - wartości górnych granic klas. Poza tym można zauważyć, że ilość zliczeń dla klasy położonej bliżej wartości średniej może być mniejsza niż dla klasy leżącej dalej i nie oznacza to dużych błędów, gdyż po zwiększeniu ilości pomiarów prawdopodobieństwo tych wyników znacznie się zmniejsza.

---