![]()
, j - gęstość prądu; E - natężenie pola elektrycznego; σ - przewodnictwo
Nr ćwicz. 201 |
Data
|
Paweł Matuszak |
wydział elektryczny |
Semestr II |
E9 1 |
mgr Janusz Rzeszutek |
przygotowanie: |
wykonanie: |
ocena: |
||
Wyznaczanie zależności przewodnictwa od temperatury
dla półprzewodników i przewodników
Prawo Ohma stwierdza, że:
![]()
, j - gęstość prądu; E - natężenie pola elektrycznego; σ - przewodnictwo
Przewodnictwo elektryczne określone jest wzorem: ![]()
n, p - koncentracje nośników; μn, μp - ruchliwość nośników.
Ponieważ koncentracja i ruchliwość zależą od temperatury i rodzaju materiału, więc przewodnictwo elektryczne także zależy od tych czynników. O zależności temperaturowej przewodnictwa w metalach decyduje tylko zmniejszanie się ruchliwości wraz ze wzrostem temperatury (koncentracja nośników - elektronów - jest bardzo duża i nie zależy od temperatury). Zależność temperaturową wyraża się poprzez opór: (R∼1/σ): ![]()
,
R0 - opór w temperaturze T0 ; α - średni współczynnik temperaturowy.
W półprzewodnikach decydujący wpływ na przewodnictwo ma koncentracja nośników. W przypadku półprzewodników samoistnych koncentracja elektronów i dziur jest taka sama i wynosi: ![]()
Eg - szerokość pasma zabronionego.
Natomiast w półprzewodnikach domieszkowych koncentracje określone są poprzez poziomy energetyczne (zależnie od typu półprzewodnika) Ed - donorowy, Ea - akceptorowy, oraz poprzez temperaturę:
![]()
.
Uwzględniając powyższe równania otrzymujemy wzór na temperaturową zależność przewodnictwa dla półprzewodników: ![]()
,
Edom jest jedną z wielkości Ed lub Ea zależnie od typu półprzewodnika.
W odpowiednio niskich temperaturach można zaniedbać w powyższym wzorze pierwszy składnik, natomiast w wysokich temperaturach (po nasyceniu poziomów domieszkowych) można zaniedbać składnik drugi. Odpowiednio dla tych dwóch przypadków wzór przyjmie postać:
![]()
.
Logarytmując jeden z powyższych wzorów otrzymamy zależność: ![]()
Zasada pomiaru
Pomiarów oporu półprzewodnika i przewodnika dokonuje się w różnych temperaturach. Badane materiały umieszczone są w ultratermostacie, a ich opory mierzy się przy pomocy mostka Wheatstone'a i liczy ze wzoru: ![]()
Błąd ΔRX liczymy ze wzoru: 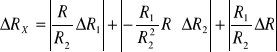
Przy czym ΔR = 0,1 [Ω]
Natomiast ΔR1 i ΔR2 dobieramy z tabelki:
Pomiary:
Dla przewodnika: ![]()
ΔR1 = 0,001 [Ω] ΔR2 = 0,003 [Ω]
T [oC] |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
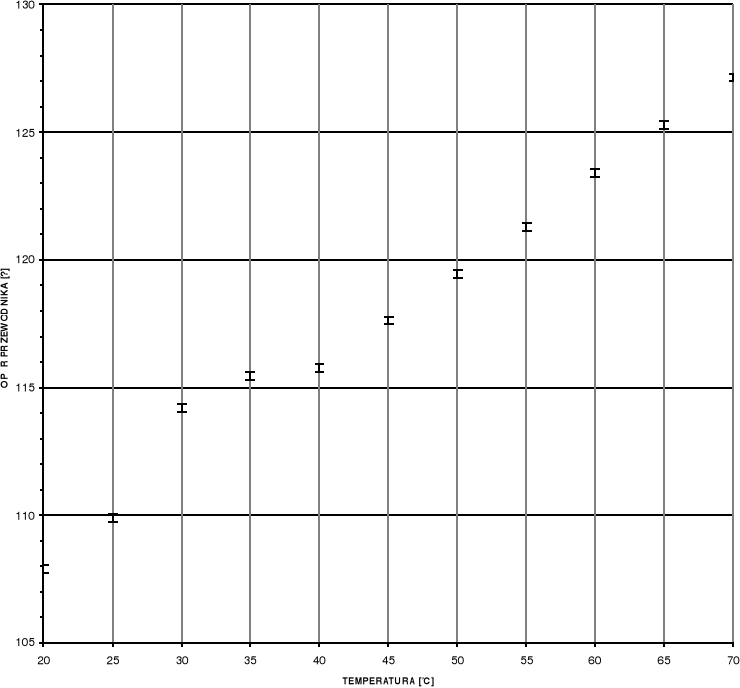
Rukł [Ω] |
1079,1 |
1098,9 |
1142,1 |
1154,5 |
1157,6 |
1176,3 |
1194,7 |
1212,9 |
1234,3 |
1253,0 |
1271,3 |
RX [Ω] |
107,91 |
109,89 |
114,21 |
115,45 |
115,76 |
117,63 |
119,47 |
121,29 |
123,43 |
125,30 |
127,13 |
ΔRX [Ω] |
0,14 |
0,14 |
0,15 |
0,15 |
0,15 |
0,15 |
0,16 |
0,16 |
0,16 |
0,16 |
0,17 |
Dla półprzewodnika: ![]()
ΔR1 = 0,03 [Ω] ΔR2 = 0,001 [Ω]
T [oC] |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
Rukł [Ω] |
3019,3 |
2428,4 |
1977,2 |
1609,0 |
1329,2 |
1102,0 |
911,2 |
753,6 |
636,2 |
531,0 |
454,1 |
RX [Ω] |
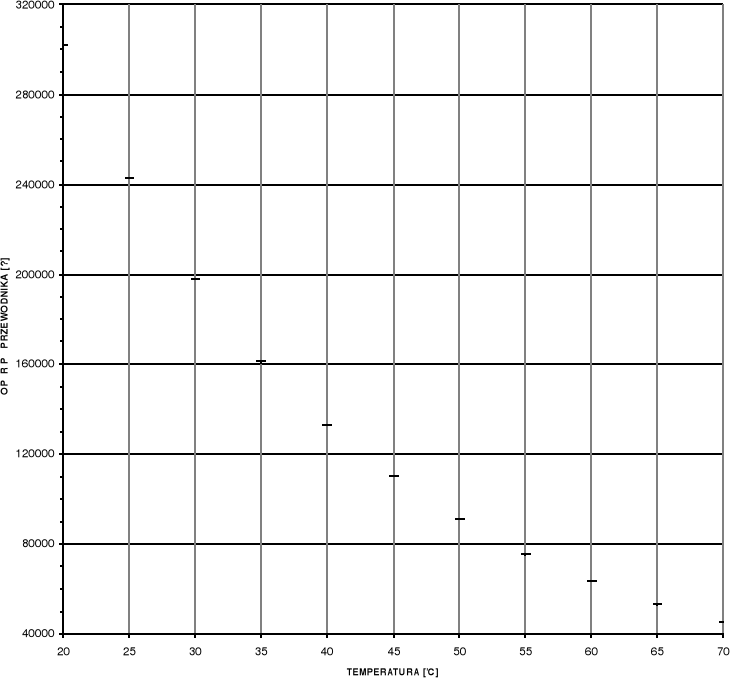
301930 |
242840 |
197720 |
160900 |
132920 |
110200 |
91120 |
75360 |
63620 |
53100 |
45410 |
ΔRX [Ω] |
403 |
326 |
244 |
219 |
183 |
153 |
129 |
108 |
93 |
79 |
69 |
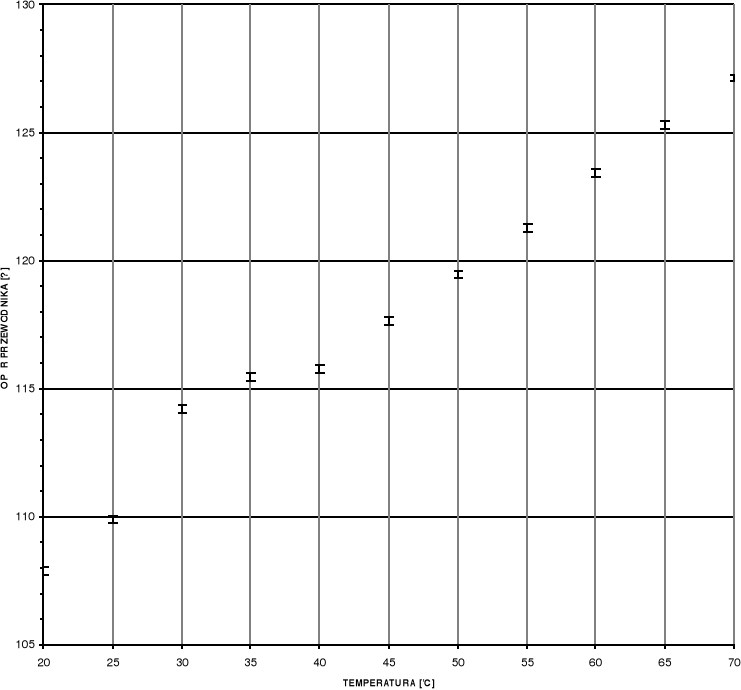
Wykres zależności oporu od temperatury dla przewodnika
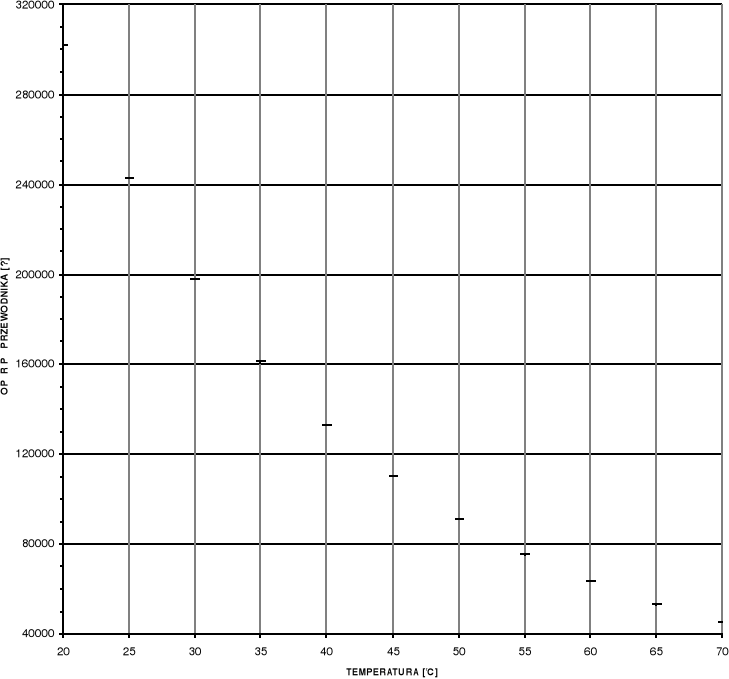
Wykres zależności oporu od temperatury dla półprzewodnika
Sporządzam dla półprzewodnika tabelę i wykres zależności ![]()
od ![]()
T [oC] |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
T [K] |
293 |
298 |
303 |
308 |
313 |
318 |
323 |
328 |
333 |
338 |
343 |
RX [Ω] |
301930 |
242840 |
197720 |
160900 |
132920 |
110200 |
91120 |
75360 |
63620 |
53100 |
45410 |
1/T [1/K] |
0,003413 |
0,003356 |
0,003300 |
0,003247 |
0,003195 |
0,003145 |
0,003096 |
0,003049 |
0,003003 |
0,002959 |
0,002915 |
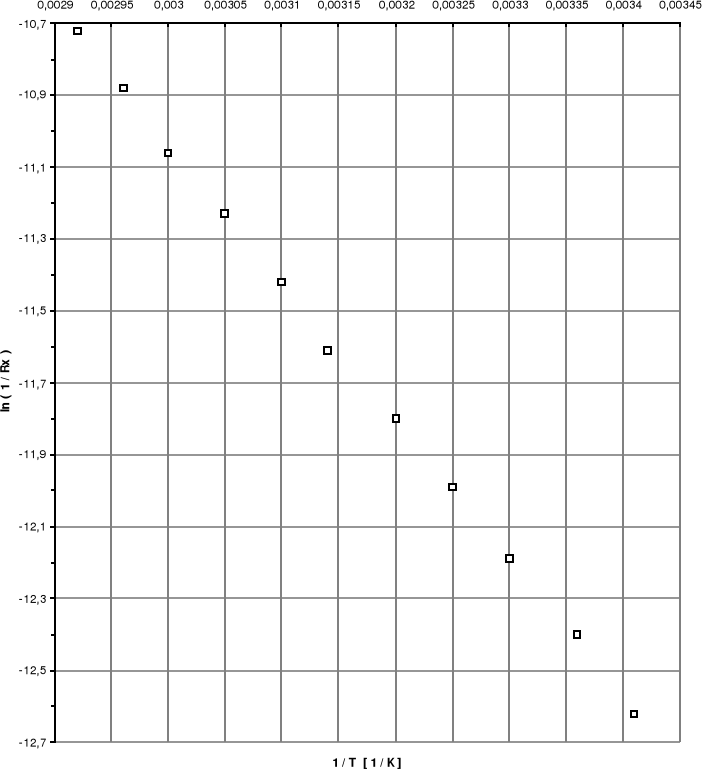
ln(1/RX ) |
-12,62 |
-12,4 |
-12,19 |
-11,99 |
-11,8 |
-11,61 |
-11,42 |
-11,23 |
-11,06 |
-10,88 |
-10,72 |
Współczynnik nachylenia prostej ln(1/R)=f(1/T) obliczony metodą regresji wynosi:
a = -3820 a= 1,27
Poziom domieszkowy będzie zatem równy:
![]()
[J] = 0,65842 [eV]
Błąd wyznaczenia poziomu domieszkowego: ![]()
3,5*10-23 [J] = 0,00022 [eV]
Wynik: E = 10548 ± 3,5 [J] = 0,65842 ± 0,00022 [eV]
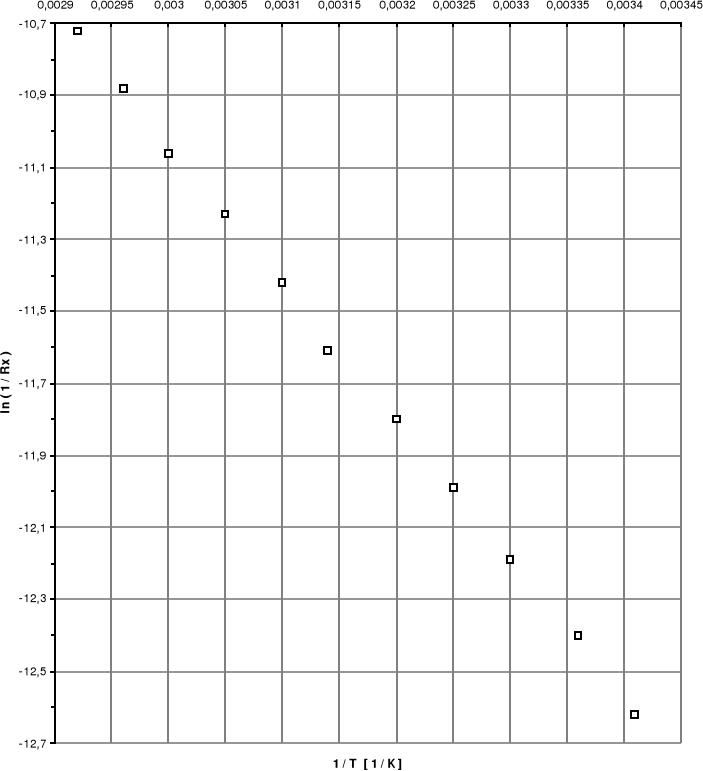
Wykres zależności ln ( 1 / Rx) od 1 / T
Wnioski
Niedokładność pomiarów jest w głównej mierze spowodowana sposobem mierzenia temperatury, a dokładnie tym, że ultratermostat nie mierzył temperatury wody z przewodnikiem i półprzewodnikiem, lecz samej przystawki, w związku z czym temperatura rzeczywista badanej próbki różniła się od wskazań ultratermostatu. Dodatkowo trudność sprawiało utrzymanie stałego poziomu temperatury, co utrudniało odczyt.
R [Ω] |
103 |
102 |
101 |
100 |
ΔR [Ω] |
0,03% |
0,03% |
0,03% |
0,1% |