Statystyka - ćwiczenia laboratoryjne

Literatura podstawowa:

1. Maliński M., Szymszal J.: Współczesna statystyka matematyczna w medycynie w arkuszach kalkulacyjnych. Wyd. Śląskiej Akademii Medycznej w Katowicach, Katowice 1999

2. Aczel A. D.: Statystyka w zarządzaniu. PWN, Warszawa 2005

Literatura zalecana

1. Stasiewicz S., Rusnak Z., Siedlecka U.: Statystyka - elementy teorii i zadania, Wyd. Akademii Ekonomicznej we Wrocławiu, Wrocław 1999

2. Sobczyk M.: Statystyka, Wyd. Uniwersytetu Marii Curie - Skłodowskiej, Lublin 2000

3. Greń J.: Statystyka matematyczna, Modele i zadania, PWN, Warszawa 1984

Wzory:

• ŚREDNIA ARYTMETYCZNA:
  lub
  ,

gdzie
-wartości, które przyjmuje cecha ,
-częstości.

• MEDIANA:
  - wartość cechy, która rozdziela uporządkowany szereg wartości cechy na dwie równe grupy: pierwszą zawierającą elementy z wartościami cechy
  i drugą zawierającą elementy z wartościami cechy
  .

Dla cechy skokowej: gdy n- nieparzyste (n=2k+1) , to
, gdy n- parzyste (n=2k ) , to
.

Dla cechy ciągłej medianę znajdujemy korzystając z warunku
. Znajdujemy najpierw przedział

w którym jest mediana, korzystając z warunku
,
a wartość mediany ze wzoru:

,

gdzie
-częstość względna przedziału mediany
.

• MODA (dominanta):
  

Dla cechy skokowej jest to ta wartość cechy, której odpowiada największa częstość .

Dla cechy ciągłej znajdujemy najpierw przedział, w którym jest moda, tzn. taki przedział
któremu odpowiada największa częstość, a wartość mody znajdujemy ze wzoru:

,

gdzie
- częstość przedziału mody,
- częstość przedziału poprzedzającego przedział mody,

- częstość przedziału następującego po przedziale mody.

• 
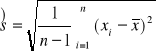
  oraz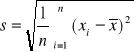
  odchylenie standardowe (określa przeciętne zróżnicowanie poszczególnych wartości cechy od wartości średniej)

• 
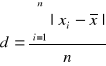
  odchylenie przeciętne (określa o ile jednostki danej zbiorowości różnią się średnio, ze względu na wartość cechy, od średniej arytmetycznej)

• 
  typowy klasyczny obszar zmienności (w obszarze tym mieszczą się wartości cechy około 2/3 wszystkich jednostek badanej zbiorowości statystycznej)

• 
  obszar zmienności ( rozstęp) (jest miarą charakteryzującą empiryczny obszar zmienności badanej cechy-nie daje inf.o zróżnicowaniu)

• 
  współczynnik zmienności ( klasyczny, oparty na odchyleniu standardowym

)( jeżeli <10%, to cechy wykazują zróżnicowanie statystycznie nieistotne)

• 
  klasyczny współczynnik asymetrii, gdzie moment centralny trzeciego rzędu oblicza się dla szeregu szczegółowego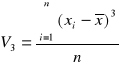
  ,

• 
  - szeregi symetryczne

- asymetria prawostronna

- asymetria lewostronna

wskaźnik skośności

współczynnik skośności Pearsona

• 
  współczynnik skupienia (kurtoza)( jest miarą koncentracji- im większe jest zróżnicowanie, tym mniejsza jest koncentracja) - Małe wartości wskazują na spłaszczenie rozkładu zbiorowości względem badanej zmiennej.

Zestaw 1

Z adanie 1. Wyznacz średnią arytmetyczną zestawu danych:

1. Ilość punktów uzyskanych przez sześć osób z testu: 10, 12, 14, 15, 17 [szereg szczegółowy] (Excel: wstaw-funkcje-statystyczne-średnia lub formuły-wiecej funkcji-statystyczne-średnia)

2. W 20 - osobowej grupie studentów zanotowano następujące oceny

Ocena	2	3	4	5
Liczba studentów	1	9	6	4

[szereg rozdzielczy punktowy]

3. Grupę 40 pacjentów pewnego szpitala, będących po pierwszym zawale serca, zbadano ze względu na wiek. Zebrane informacje przedstawiono w postaci szeregu rozdzielczego

Wiek w latach	40 - 45	45-50	50-55	55-60	60-65	65-70	70-75
Liczba pacjentów	4	5	6	11	7	5	2

[szereg rozdzielczy przedziałowy]

Zadanie 2. Wyznacz medianę, kwartyl pierwszy, kwartyl trzeci, maksimum, minimum, dominantę zestawu danych:

4, 4, 4, 5, 6, 7, 8, 8, 9, 10, 12 (Excel: wstaw-funkcje-statystyczne-kwartyl lub formuły-wiecej funkcji-statystyczne-kwartyl)

Zadanie 3. Oblicz odchylenie standardowe tego zestawu danych.

38 kg, 40 kg, 42 kg, 42 kg, 45 kg, 48 kg, 50 kg, 51 kg. (Excel: wstaw-funkcje-statystyczne-odch. standardowe lub formuły-wiecej funkcji-statystyczne- odch. standardowe)

Zadanie 4. Na podstawie 9 pomiarów poziomu mocznika u chorych na łuszczycę obliczyć wartość punktowego estymatora odchylenia standardowego. (Excel: wstaw-funkcje-statystyczne-wariancja lub formuły-wiecej funkcji-statystyczne- wariancja)

	Poziom mocznika [g/l]
1	0,47
2	0,46
3	0,49
4	0,48
5	0,46
6	0,46
7	0,49
8	0,51
9	0,47

Zadanie 5. Na podstawie 11 pomiarów poziomu cholesterolu całkowitego (podanego w mg%) wyznaczyć wartość nieobciążonego estymatora wariancji.(Excel: wstaw-funkcje-statystyczne-wariancja lub formuły-wiecej funkcji-statystyczne- wariancja)

	Cholestrol [mg%]
1	202
2	145
3	310
4	410
5	220
6	180
7	160
8	157
9	256
10	283
11	190

Zadanie 6. Czas dojazdu na uczelnię dla grupy badanych studentów był następujący ( w minutach)

20, 35, 35, 70, 50, 45, 30, 35

Przeprowadź wszechstronną analizę czasu dojazdu na uczelnię dla tej grupy studentów.

Zadanie 7. Dysponujemy informacjami o liczbie spóźnień na zajęciach studentów I roku

Liczba spóźnień	0	1	2	3	4	5
Liczba studentów	50	100	150	120	60	20

Przeprowadź wszechstronną analizę liczby spóźnień na zajęcia.