Podstawowe wzory trygonometrii sferycznej:

Sinusowe:

Cosinusowe:

cos a = cos b *cos c + sin b * sin c * cos A

cos b = cos c * cos a + sin c * sin a * cos B

cos c = cos a * cos b + sin a * sin b * cos C

,,Cosinus boku równa się sumie iloczynu cosinusów pozostałych boków oraz iloczynowi sinusów tych boków i cosinusa kąta przeciwległego”

cosA= -cosBcosC+sinBsinCcosa

cosB = -cosAcosC+sinCsinAcosb

cosC = -cosAcosB+sinAsinBcosc

3. Sinusowo-cosinusowe:

sin a * cos B = cos b * sin c - sin b *cos c * cos A

sin a * cos C = cos c * sin b - sin c *cos b * cos A

sin b * cos C = cos c * sin a - sin c *cos a * cos B

sin b * cos A = cos a * sin c - sin a *cos c * cos B

sin c * cos A = cos a * sin b - sin a *cos b * cos C

sin c * cos B = cos b * sin a - sin b *cos a * cos C

sin A * cos b = cos B * sin C + sin B * cos C * cos a

sin A * cos c = cos C * sin B + sin C * cos B * cos a

sin B * cos c = cos C * sin A + sin C * cos A * cos b

sin B * cos a = cos A * sin C + sin A * cos C * cos b

sin C * cos a = cos A * sin B + sin A * cos B * cos c

sin C * cos b = cos B * sin A + sin B * cos A * cos c

4. Cosinusowe - albataniego (dla kąta):

cos a = cos b * cos c + sin b * sin c * cos A

cos b = cos a * cos c + sin a * sin c * cos B

cos c = cos a * cos b + sin a * sin b * cos C

5. Cotangensowe:

ctg A * sin B = ctg a * sin c - cos B * cos c

ctg A * sin C = ctg a * sin b - cos C * cos b

ctg B * sin C = ctg b * sin a - cos C * cos c

ctg B * sin A = ctg b * sin c - cos A * cos c

ctg C * sin A = ctg c * sin b - cos A * cos b

ctg C * sin B = ctg c * sin a - cos B * cos a

6. Połówkowe:

2s = a + b + c 2S = A + B + C

7. 
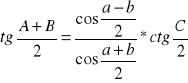
   Analogie Nepera:

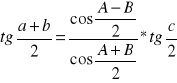
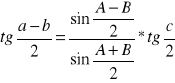
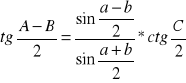
Nadmiar sferyczny

R=6370km.

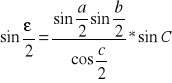
ε = P / R² * ρ”

2s = a + b + c

Wzory Borda dla kątów - wzory połówkowe:

Jest to alternatywa wzoru cosinusów dla boku.

Wzory Borda są często wykorzystywane w astronomii geodezyjnej, gdy znane są wszystkie boki trójkąta sferycznego, a poszukiwane są jego kąty.

niech a+b+c=2s

Wprowadzając wielkość pomocniczą

gdzie r - promień okręgu wpisanego w trójkąt sferyczny o bokach a, b, c

Wzory połówkowe zapiszemy

Wzory Borda dla boków (wzory połówkowe dla boków):

A+B+C=2S

gdzie RΔ - promień okręgu opisanego na trójkącie sferycznym obliczamy z zależności:

tg²RΔ=-cosS/(cos(S-A)cos(S-B)cos(S-C)
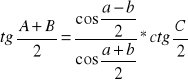
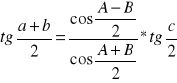
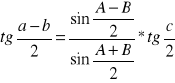
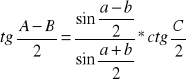
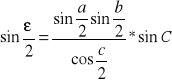