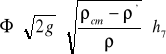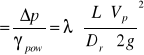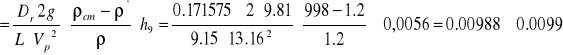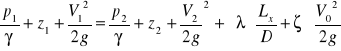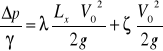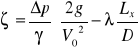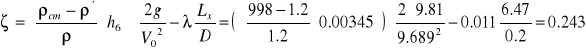2004/2005 sem letni

Wykonano: 04-03-2005

Prowadzący: Z.R. Komarzeniec

Sprawozdanie z laboratorium Mechaniki płynów

Temat 16: Przepływ w przewodach wentylacyjnych.

1 Cel ćwiczenia:

• wyznaczanie doświadczalne współczynnika oporów liniowych λ od liczby Reynoldsa λ=λ(Re).

• wyznaczanie doświadczalne zależności współczynnika oporów miejscowych
  od liczby Reynoldsa
  =
  (Re) dla łuku segmentowego.

• Objętościowe natężenie przepływu powietrza Q

2 Dane:

- średnica pierścienia Recknagla D=200mm=0.2m

- temperatura otoczenia t=21^oC

stąd:

- gęstość cieczy manometrycznej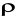
_cm=998 kg/m³

- gęstość powietrza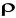
^'=
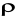
=1.2 kg/m³

- kinematyczny współczynnik lepkość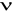
=15.06*10^-6 m²/s

- współczynnik prędkości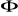
=1

- przyspieszenie ziemskie g=9.81 m²/s

- wymiary przewodu a=0.2004m b=0.15m

średnica równoważna przewodu D_r=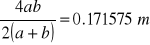

- długość prostego odcinka przewodu L=9.15m

długość przewodu na którym zainstalowany jest luk segmentowy L_x=6.47m

3. Obliczenia:

• prędkość strugi V i natężenie strumienia powietrza Q.

V₀ =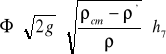
=

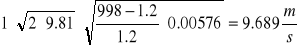
A₀ =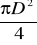
=

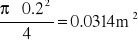
Q = V₀ A =

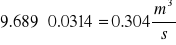
A_p =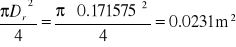

V_p =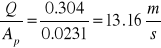

gdzie:

V₀ - prędkość w przewodzie kołowym

V_p - prędkość w przewodzie prostokątnym

A₀ - pole przekroju przewodu kołowego

A_p - pole przekroju przewodu prostokątnego

Q - natężenie strumienia powietrza

h₇ - wysokość słupa wody w mikromanometrze do mierzenia obj. natężenia przepływu

Natężenie przepływu Q; Prędkości przepływu w
przewodach okrągłych Vo i prostokątnych Vp
nr	h 7	h 7śr	Vo	Q	Vp
1	5.75	0,00576	9,6887	0,3042	13,1699
						5.76
	2					2.09	0,00211	5,8640	0,1841	7,9710
						2.12
	3					0.85	0,00085	3,7219	0,1169	5,0592
						0.84
	4					1.65	0,00164	5,1698	0,1623	7,0274
						1.63
	5					4.60	0,00463	8,6865	0,2728	11,8076
						4.65
	6					2.25	0,00224	6,0420	0,1897	8,2129
						2.23
	7					5.00	0,00499	9,0179	0,2832	12,2581
						4.98
	8					5.10	0,00511	9,1257	0,2865	12,4046
						5.12
	9					5.37	0,00536	9,3462	0,2935	12,7044
						5.34
	10					6.57	0,00656	10,3397	0,3247	14,0548
						6.55
	11					0.82	0,00081	3,6333	0,1141	4,9387
						0.79
	12					1.22	0,00124	4,4954	0,1412	6,1106
						1.25

• współczynnik oporów liniowych, liczba Reynoldsa.

H_L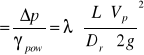

H_L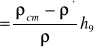

λ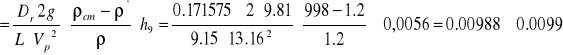

Re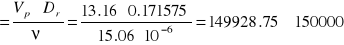

gdzie:

λ - współczynnik oporów liniowych

h_g - wysokość słupa wody w mikromanometrze do mierzenia oporów liniowych

Re - liczba Reynoldsa

Straty liniowe
nr	h 9	h 9śr	λ	Re
1	4.68	0,00560	0,0099	150041,95
					5.52
	2				2.37	0,00235	0,0113	90811,88
					2.32
	3				1.30	0,00130	0,0155	57638,27
					1.29
	4				2.09	0,00209	0,0129	80061,44
					2.09
	5				4.78	0,00480	0,0105	134521,58
					4.81
	6				2.61	0,00252	0,0114	93567,59
					2.43
	7				5.09	0,00509	0,0104	139653,47
					5.09
	8				5.21	0,00521	0,0104	141322,69
					5.20
	9				5.40	0,00539	0,0102	144738,43
					5.38
	10				6.51	0,00650	0,0101	160122,87
					6.49
	11				1.16	0,00117	0,0147	56265,73
					1.18
	12				1.59	0,00159	0,0130	69616,52
					1.58

• współczynnik oporów miejscowych na luku segmentowym i liczba Reynoldsa.

gdzie:

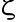
- współczynnik oporów miejscowych na luku segmentowym

h₆ - wysokość słupa wody w mikrometrze do mierzenia oporów miejscowych na łuku segmentowym

*
odczytujemy z wykresu wcześniej wyznaczonej zależności
=
(Re)

Straty miejscowe
nr	h 6	h 6śr			Re
1	3.39	0,00345	0,0110	0,2432	128668,14
						3.50
	2					1.85	0,00188	0,0120	0,5029	77875,53
						1.90
	3					1.25	0,00108	0,0140	0,8178	49427,57
						0.9
	4					1.62	0,00160	0,0130	0,5551	68656,51
						1.59
	5					3.50	0,00345	0,0110	0,3893	115358,68
						3.40
	6					1.98	0,00196	0,0120	0,4869	80238,68
						1.94
	7					3.77	0,00381	0,0110	0,4077	119759,52
						3.85
	8					3.87	0,00388	0,0110	0,4035	121190,96
						3.90
	9					4.20	0,00421	0,0110	0,4297	124120,12
						4.22
	10					4.90	0,00492	0,0100	0,4266	137313,01
						4.94
	11					1.10	0,00108	0,0130	0,9129	48250,55
						1.05
	12					1.30	0,00132	0,0130	0,6440	59699,49
						1.34

4 Wnioski:

Na podstawie wykonanych przez nas pomiarów i obliczeń sporządziliśmy wykresy zależności oporów liniowych od liczby Reynoldsa λ=λ(Re) oraz zależności oporów miejscowych na łuku segmentowym od liczby Reynoldsa ζ=ζ(Re).

Po porównaniu naszkicowanego przez nas wykresu zależności λ=λ(Re) z wykresem Colebrooka-White'a możemy zauważyć że pomiary wykonywane były w zakresie przepływu turbulentnego. Wykres ten przebiega poniżej linii wyznaczającej strefę rur hydraulicznie gładkich co oznacza iż przyścienna warstwa laminarna przykrywa nierówności ścianki a zatem współczynnik oporów liniowych λ zależy tylko od Re. Wartości współczynnika oporów liniowych jakie obliczyliśmy z wykonanych pomiarów wahają się między 0,0099 a 0,0155. Zależność liczby λ pokazaliśmy na wykresie nr1 . Zauważyliśmy że na początku następuje szybki spadek a później stabilizuje się, w miarę ze wzrostem liczby Re z czego możemy wnioskować iż wykres został sporządzony prawidłowo, gdyż, odnosząc się do wykresu Colebrooka-White'a , za linią Re granicznego wykresy te zaczynają biec równolegle.

Wartości współczynnika oporów miejscowych zamieściliśmy w tabeli nr3. Obliczenia z wykonanych pomiarów wahają się od 0,2432 do 0,9131 . Opory te w przypadku łuku segmentowego powinny wahać się między 0,3 i 0,45.

Otrzymane przez nas wyniki, współczynników oporów liniowych i miejscowych, w niektórych przypadkach odbiegają od wartości tablicowych. Na tej podstawie twierdzimy, ze przeprowadzone pomiary zostały wykonane niedokładnie. Prawdopodobnie spowodowane jest to zbyt krótkim czasem stabilizacji wskazań mikromanometrów, w wyniku czego otrzymaliśmy błędne( niektóre) wyniki pomiarów. Wyników, które według naszej oceny były nie dokładne nie uwzględnialiśmy podczas sporządzania żądanych wykresów.

Po porównaniu sporządzonych przez nas wykresów zależności λ=λ(Re) i ζ=ζ(Re) z normami ( wykres Colebrooka-White'a , wartości ζ dla łuku segmentowego, wykresy zależności ζ=ζ(Re)) zawartymi w podręcznikach, możemy stwierdzić że są one prawidłowe.

---