POLITECHNIKA ŚLĄSKA W GLIWICACH

WYDZIAŁ ORGANIZACJI I ZARZĄDZANIA

Katedra Informatyki i Ekonometrii

Badania operacyjne

Projekt nr 1

Optymalizacja liniowa

Wykonał: Hubert Skrzypulec

Data: 17.04.2008

Kierunek: ZiIP 2.2

Miasto: Zabrze

Funkcja celu: (a+8)x₁+ (b+10)x₂ min/max

Ograniczenia:

1. (2b+16)x₁+ (2c+18)x₂ ≤ 8a+8b+20

2. (a+4)x₁+ (b+6)x₂ ≤ 6(a+c+10)

3. (c+10)x₁+ (a+3)x₂≥ 2(b+c+2)

4. (a+c)x₁ ≤ (b+c+2)x₂

Po podstawieniu parametrów: a=4, b=1, c=3, otrzymuję następujący model, który traktuję jako model dualny

Fc: 12x₁+ 11x₂ max

Ograniczenia:

18x1+ 24x2 ≤ 60 8x1+ 7x2 ≤ 102 13x1+ 7x2≥12 7x1 ≤ 6x2 x1,x2≥0

0≤60-18x1-24x2 0≤102-8x1-7x2 0≤-12+13x1+7x2 0≤-7x1+6x2

Zadanie:

Huta Batory produkuje dwa gatunki stali: stal konstrukcyjną (x₁) i stal nierdzewną (x₂). Do produkcji tych stali wykorzystuje: żelazo, węgiel i chrom.

Zużycie tych surowców (na wyprodukowanie tysiąca ton stali), w ciągu doby, dopuszczalne limity zużycia surowców oraz zyski ze sprzedaży podaje tabela:

Wyrób	Zużycie surowców do produkcji stali na dobę			Zysk jednostkowy
		Żelazo	Węgiel		Chrom
Stal konstrukcyjna	18	8	13	12
Stal nierdzewna	24	7	7	11
Limit zużycia surowców	60	102	12

Ile należy wyprodukować stali konstrukcyjnej, a ile nierdzewnej, aby nie przekraczając limitów zużycia surowców zmaksymalizować zysk ze sprzedaży.

Ze względu na zróżnicowanie produkcji należy przyjąć, że na 6 ton stali nierdzewnej przypada 7 ton stali konstrukcyjnej.

Rozwiązanie metodą graficzną:

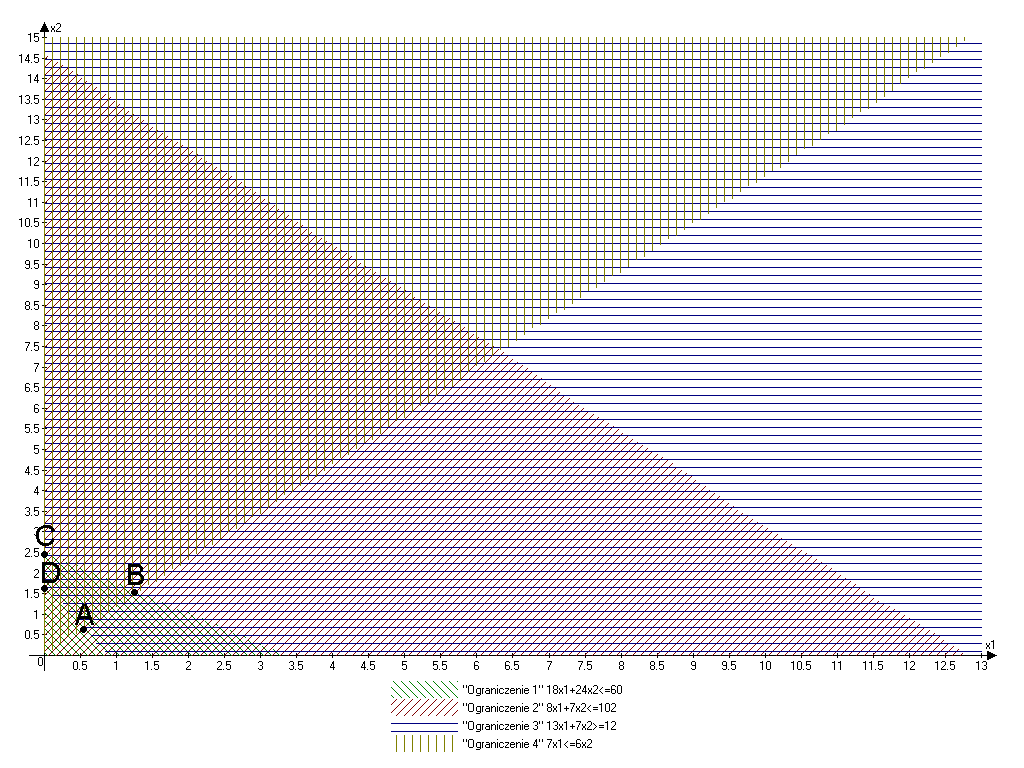
Obliczam współrzędne punktu A Stąd współrzędne punktu	Obliczam współrzędne punktu B Stąd współrzędne punktu
Obliczam współrzędne punktu C Stąd współrzędne punktu	Obliczam współrzędne punktu D Stąd współrzędne punktu

Podstawiam otrzymane wartości x₁ i x₂ do funkcji celu, aby znaleźć optymalne rozwiązania:

1. 
   

Fc_A:

2. 
   

Fc_B:
MAX

3. 
   

Fc_C:

4. 
   

Fc_D:

Na tej podstawie nasze optymalne rozwiązanie (maksymalizujące zysk) to: produkcja 1304 tony stali konstrukcyjnej, i 1521 ton stali nierdzewnej, otrzymując zysk 12521 zł.

Model dualny

Funkcja celu modelu dualnego: G: 60y₁+102y₂-12y₃+0y₄ min

Ograniczenia:

1. 18y₁+8y₂-13y₃+8y₄-12≥0

2. 24y₁+7y₂-7y₃-6y₄-11≥0

Podstawiam do równań wartość x₁ i x₂

1. y₁(60-18x₁-24x₂₎=0

2. y₂(102-8x₁-7x₂)=0

3. y₃(-12+13x₁+7x₂)=0

4. y₄(-7x₁+6x₂)=0

5. x₁(18y₁+8y₂-13y₃+8y₄-12)=0

6. x₂(24y₁+7y₂-7y₃-6y₄-11)=0

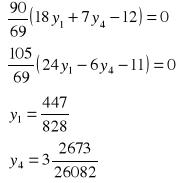
Podstawiam otrzymane wyniki do funkcji celu modelu dualnego:

G:

Rozwiązanie modelu liniowego za pomocą programu Excel (dodatek Solver)

Rozwiązanie modelu dualnego za pomocą programu Excel (dodatek Solver)

Odpowiedź:

W celu zmaksymalizowania zysków, Huta Batory powinna w ciągu doby produkować 1304 tony stali konstrukcyjnej oraz 1521 ton stali nierdzewnej. W ten sposób wypracuje 12521 zł zysku.

Strona 5 z 7