Kx + Ky = ![]()
= całkowity, dostępny zasób kapitału;
Efektywność produkcji
i równowaga ogólna
na rynkach doskonale konkurencyjnych
Efektywność produkcji
Maksymalizacja użyteczności nad krzywą możliwości produkcyjnych
Optymalność w sensie Pareta przy więcej niż jednym konsumencie
Równowaga ogólna w gospodarce doskonale konkurencyjnej
Statyka porównawcza w analizie równowagi ogólnej
♣
Efektywność produkcji
Efektywna alokacja czynników między różnymi procesami produkcji oznacza, że nie można wyprodukować więcej jednego dobra bez zmniejszenia produkcji innego dobra. Efektywna alokacja czynników oznacza, że został spełniony podstawowy warunek efektywności produkcji.
Skrzynka Edgeworth'a
Funkcje produkcji: x = x(Kx, Lx) i y = y(Ky, Ly)
Gdzie:
Kx + Ky = ![]()
= całkowity, dostępny zasób kapitału;
Lx + Ly = ![]()
= całkowity, dostępny zasób pracy.
Rys. 14.1, 14.2.
|
|
Zbiór efektywnej produkcji, czyli krzywa kontraktowa
Rys. 14.3 - krzywa kontraktowa:
MRTSx = MRTSy ⇒ MPLx/MPKx = MPLy/MPKy
Wiemy, że : MRTS = ![]()
. Ponieważ MRTSy są równe stosunkowi cen czynników, to z każdym punktem styczności izokwant związany jest stosunek cen, któremu odpowiada alokacja czynników osiągana w równowadze doskonale konkurencyjnej na rynkach czynników. Jest to matematycznie równoważne stwierdzeniu, że każdy punkt z krzywej kontraktowej może być osiągnięty w równowadze doskonale konkurencyjnej dla danego zbioru wyposażeń początkowych i danego stosunku cen. Pokazuje to Rys. 14.4: w punkcie A na krzywej efektywności produkcji założony stosunek cen czynników wynosi: w1/r1, a w punkcie B: w2/r2.
Przykład
Aby wykazać, że MRTSy dla dwóch dóbr równają się sobie, maksymalizujemy produkcję jednego dobra, np. X, przy ograniczeniu, że wielkość produkcji y nie jest mniejsza od zadanego poziomu i przy ograniczeniach czynników:
max x(Kx, Lx)
p.w.: y = y(Ky, Ly)
Kx + Ky = ![]()
Lx + Ly = ![]()
.
Łączymy trzy ograniczenia wstawiając ograniczenia czynników do funkcji produkcji y:
y = y(![]()
- Kx, ![]()
- Lx).
Lagrangian:
![]()
Warunki pierwszego rzędu:
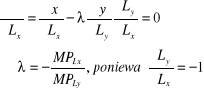
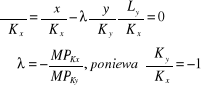
Rozwiązując dla λ:
![]()
.
Po uporządkowaniu powyższego wyrażenia otrzymujemy:
![]()
.
Wynika z tego, że można osiągnąć efektywność produkcji dwóch dóbr dzięki zrównaniu MRTSów dwóch funkcji produkcji. Na przykład:
x = (Kx)1/2 (Lx)1/2 oraz y = (Ky)1/4 (Ly)3/4 .
MRTSx = Kx / Lx
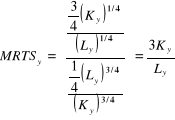
.
![]()
.
Rozwiązując powyższe równanie dla Kx:
![]()
![]()
: Krzywa kontraktowa.
Liniowa i nieliniowa krzywa kontraktowa
Z wyprowadzonego wzoru na krzywą kontraktową wynika, że jest ona nieliniowa.
Uogólniając:
Krzywa kontraktowa jest linią prostą, gdy firmy mają stałe i jednakowe stosunki kapitału do pracy.
Krzywa kontraktowa jest nieliniowa, gdy firmy mają różny stosunek kapitału do pracy.
W przykładzie mieliśmy: MRTSx = Kx / Lx i MRTSy = 3Ky / Ly , czyli w firmie X stosunek kapitału do pracy równa się mrts, a w firmie Y stosunek ten równa się 1/3 jej MRTS. Wynika z tego, że Ky/Ly = (1/3) MRTSy. Wzdłuż krzywej kontraktowej stosunek kapitału do pracy w firmie Y zawsze jest mniejszy niż w firmie X.
Jeżeli funkcję produkcji firmy X opisywałby wzór:
Kx1/2 Lx1/2, a firmy Y: 2 Ky1/2 Ly1/2 , to w obu firmach byłby taki sam stosunek kapitału do pracy wzdłuż prostoliniowej krzywej kontraktowej:
![]()
.
Rozwiązując dla Kx:
![]()
: funkcja liniowa.
Granica możliwości produkcyjnych
Jeśli „wyjmiemy” krzywą kontraktową ze skrzynki Edgeworth'a i umieścimy ją w układzie współrzędnych, w którym wzdłuż osi poziomej mierzymy wielkość produkcji X, a wzdłuż pionowej - Y, to skonstruujemy krzywą (funkcję) przedstawiającą wszystkie efektywne kombinacje X i Y, jakie w gospodarce można wyprodukować przy danej technice i zasobie czynników produkcji. Jest to krzywa możliwości produkcyjnych (PPF - production possibililty frontier) - rys. 14.5.
Liniowa i nieliniowa PPF i krańcowa stopa transformacji (MRT)
Krzywa możliwości produkcyjnych może być:
-„wybrzuszona” od początku układu współrzędnych jak na rys. 14.5, gdy będzie spełniony jeden z trzech warunków: obydwie funkcje produkcji charakteryzują malejące korzyści skali; jedną funkcję charakteryzują malejące korzyści skali, a drugą - stałe; obydwie funkcje produkcji charakteryzują stałe korzyści skali, ale różne stosunki kapitału do pracy wzdłuż nieliniowej krzywej kontraktowej.
może być prostą, gdy obie funkcje produkcji mają stałe korzyści skali i równe stosunki kapitału do pracy wzdłuż liniowej krzywej kontraktowej.
może być „wybrzuszona” do początku układu współrzędnych, gdy jedna z funkcji produkcji ma rosnące korzyści skali.
Nachylenie krzywej możliwości produkcyjnych ze znakiem minus określamy mianem krańcowej stopy transformacji (MRT):
![]()
.
MRT jest stopą, zgodnie z którą gospodarka może przechodzić od produkcji Y do produkcji X w sposób efektywny dzięki przesuwaniu zasobów czynników. Przy prostoliniowej krzywej możliwości produkcyjnych MRT jest stała. Przy krzywej „wybrzuszonej” od początku układu współrzędnych MRT rośnie wraz ze wzrostem produkcji X.
Przy wzroście MRT i „wybrzuszonej” od początku układu współrzędnych krzywej transformacji jeden produkt jest względnie bardziej pracochłonny, a drugi - względnie bardziej kapitałochłonny. Kiedy oba dobra są wytwarzane w znacznych ilościach, to produkcja dobra kapitałochłonnego zatrudnia względnie dużą część kapitału, a produkcja dobra pracochłonnego zatrudnia względnie dużą część pracy dostępnej w gospodarce. Jeżeli rośnie produkcja dobra kapitałochłonnego potrzeba ograniczać stosunek kapitału do pracy aż zrówna się ze stosunkiem kapitału i pracy dostępnych w gospodarce, przy rozwiązaniu brzegowym, gdy tylko jedno dobro jest wytwarzane. Analogicznie, gdy rośnie wielkość produkcji dobra pracochłonnego, należy utrzymywać wzrost stosunku kapitału do pracy aż zrówna się ze stosunkiem ![]()
do ![]()
w drugim rozwiązaniu brzegowym. Jeżeli natomiast zmienia się stosunek kapitału do pracy wzdłuż izokwant, to z malejącej MRTS wynika, że trzeba rezygnować z coraz większych ilości dobra produkowanego we względnie małej ilości w celu uzyskania takiego samego przyrostu dobra produkowanego we względnie dużej ilości. Jeśli więc rośnie produkcja X, to MRT też rośnie, co oznacza, że w gospodarce należy rezygnować z coraz większej ilości Y w celu utrzymania takiego samego przyrostu X.
Rys. 14.6 pokazuje dlaczego MRT rośnie.
Jeżeli krzywa kontraktowa jest linią prostą, to stosunek kapitału do pracy jest taki sam niezależnie od wielkości produkcji. Produkcja każdego z dóbr może się więc zmieniać wzdłuż prostej wychodzącej z początku układu współrzędnych. W tej sytuacji jeżeli obie funkcje produkcji mają również stałe korzyści skali, to zmniejszenie produkcji Y potrzebne do stałego wzrostu X, jest również stałe. MRT jest więc stałe, a krzywa możliwości produkcyjnych jest liniowa.
Pokazuje to rys. 14.7.
Kilka przykładów
Dla liniowej krzywej kontraktowej, ![]()
uzyskanej dla funkcji produkcji:
x = Kx1/2 Lx1/2 i y = 2 Ky1/2 Ly1/2, wyznaczamy krzywą możliwości produkcyjnych. Analogicznie wyznaczamy: ![]()
. Przekształcamy funkcje produkcji x oraz y:
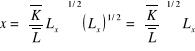
i 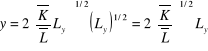
Wyrażenie na x rozwiązujemy dla Lx: 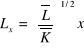
i wstawiamy do rozwiązania dla y:
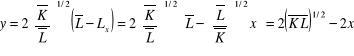
, co opisuje liniową krzywą możliwości produkcyjnych. Wyrażenie ![]()
wyznacza punkt przecięcia z osią pionową, czyli maksymalną wielkość produkcji dobra Y, a MRT = 2:
![]()
.
Wracając do przypadku nieliniowego wiemy, że krzywą kontraktową opisuje wzór: ![]()
dla funkcji produkcji: x = (Kx)1/2 (Lx)1/2 i y = (Ky)1/2 (Ly)1/2 . Pomijamy wyprowadzenia, ale spostrzegamy, że krzywa możliwości produkcyjnych musi być nieliniowa, gdyż po dokonaniu podstawienia Kx do x otrzymujemy równanie wykładnicze względem x i Lx.
Maksymalizacja użyteczności nad krzywą możliwości produkcyjnych
Każdy punkt z krzywej możliwości produkcyjnych reprezentuje efektywność produkcji. Aby dokonać wyboru któregoś z nich trzeba odwołać się do problemu efektywnej dystrybucji. Pamiętamy, że bez sfery produkcji, dystrybucja jest określona przez preferencje konsumentów i ich wyposażenia początkowe w oba dobra. Analogiczny wynik otrzymujemy w odniesieniu do produkcji, przy czym wyposażenia obejmuje czynniki, a nie produkty.
Robinson Crusoe i optymalność w sensie Pareta
Zacznijmy od gospodarki jednoosobowej. Robinson wytwarza dla siebie żywność w postaci orzechów kokosowych i ryb. Przy posiadanych narzędziach technice produkcji możemy skonstruować krzywą możliwości produkcyjnych opisującą wszystkie efektywne kombinacje produkcji obu dóbr - rys. 14.8.
Przyjmujemy, że Robinson ma preferencje dotyczące swej konsumpcji ilustrowane przez krzywe obojętności spełniające wszystkie założenia dotyczące preferencji. Jeśli Robinson maksymalizuje użyteczność, to wybiera taką kombinację orzechów i ryb, która umożliwia mu osiągnięcia najwyższej krzywej obojętności, U3 = U* w punkcie (C*, F*), w którym nachylenie krzywej obojętności równa się nachyleniu krzywej możliwości produkcyjnych. Co więcej, taka alokacja spełnia warunek efektywności produkcji (bo jest na krzywej transformacji) i optymalności w sensie Pareta (jest tylko jeden konsument) i jest Pareto superior względem każdej innej alokacji przy danej technice i zasobach czynników.
Ponieważ nachylenie krzywej obojętności ze znakiem minus jest MRS, to z maksymalizacji użyteczności wynika, że efektywna kombinacja produktów, która została wybrana zrównuje MRS z MRT: MRTFC = MRSFC. W równaniu tym zrównuje się wewnętrzna i zewnętrzna stopa wymiany wyznaczając optimum. MRT jest stopą zewnętrzną wyznaczoną przez czynniki i technikę. Przedstawia stopę, przy której gospodarka w sposób efektywny może przestawiać się z produkcji jednego dobra na produkcję drugiego dzięki realokacji czynników. MRS jest wewnętrzną stopą wymiany konsumenta. Maksymalizacja użyteczności zostaje osiągnięta, gdy nastąpi zrównanie obu stóp.
Ceny
Pamiętamy, że jeśli ceny są parametrami, to przy maksymalizacji użyteczności MRS zrównuje się ze stosunkiem cen: ![]()
. Oznacza to również ![]()
, co pokazuje rys. 14.9.
Rozwiązanie problemu decyzyjnego Robinsona
Następujący przykład pokazuje jak wyznaczyć:
alokację maksymalizującą użyteczność Robinsona przy danej krzywej możliwości produkcyjnych
zbiór cen zapewniających, że ta alokacja jest równowagą doskonale konkurencyjną.
Przyjmijmy, że orzechy i ryby są wytwarzane zgodnie z funkcjami produkcji o stałych korzyściach skali:
x = Kx1/2 Lx1/2 i y = 2 Ky1/2 Ly1/2, które przepisujemy do postaci: C = KC1/2 LC1/2 i F = 2 KF1/2 LF1/2. Niech: ![]()
i ![]()
. Po wstawieniu tych wielkości do otrzymanego wcześniej wzoru na liniową krzywą możliwości produkcyjnych (![]()
) otrzymujemy:
![]()
.
Jeżeli funkcję użyteczności Robinsona opisuje wzór: U = CF, to problem maksymalizacji użyteczności możemy zapisać następująco:
maxU = CF
p.w.: F = 400 - 2C.
Funkcja Lagrange'a przyjmuje postać:
![]()
.
Warunki pierwszego rzędu:
![]()
![]()
![]()
Rozwiązując dla λ:
(F/2) = - C ⇒ F = 2C.
Otrzymane rozwiązanie wstawiamy do trzeciego warunku koniecznego:
2C - 400 + 2C = 0,
który rozwiązujemy dla C* i otrzymany wynik wstawiamy do F = 2C:
C* = 100 oraz F* = 2(100) = 200.
Aby wyznaczyć ceny wyznaczamy MRTFC oraz MRSFC:
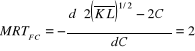
![]()
,
Tak więc: ![]()
.
Aby znaleźć ceny czynników należy najpierw określić ich alokację wstawiając ![]()
i ![]()
oraz C* = 100 i F* = 200 do 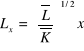
:
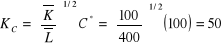
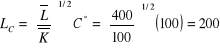
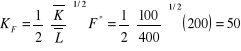
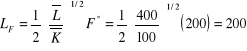
Następnie wyznaczamy MRS:
![]()
![]()
Tak więc:
![]()
.
Przyjmijmy, że ![]()
jest normalizacją. To oznacza:
![]()
.
Wiedząc, że w = pCMPLC:
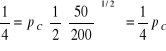
.
Rozwiązujemy powyższe równanie dla ![]()
i wyprowadzamy ![]()
:
![]()
i 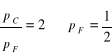
.
Ponieważ obydwie funkcje produkcji mają stałe korzyści skali, to płatności dla czynników powinny równać się wydatkom:
![]()
¼(200 + 200) + (50 + 50) = 1(100) + ½ (200)
100 + 100 = 100 + 100.
Przyjęliśmy więc, że ![]()
i znaleźliśmy wartości w równowadze:
![]()
, ![]()
, ![]()
, ![]()
,
C* = 100, F* = 200, LC = LF = 200, KC = KF = 50.
Osiągnięta równowaga osiągnęła efektywność produkcji, gdyż nie jest możliwe produkować więcej dobra bez ograniczenia produkcji innego dobra oraz konsument maksymalizuje użyteczność w niej.
Optymalność w sensie Pareta przy więcej niż jednym konsumencie
Przyjmujemy, że użyteczność osoby A znajduje się na poziomie ![]()
. Następnie maksymalizujemy użyteczność osoby B przy danej krzywej kontraktowej dla produkcji, czyli mając całkowite wielkości X i Y dostępne do dystrybucji.
Wyznaczenie optymalności w sensie Pareta graficznie
Rys. 14.10
Ceny przy dwóch konsumentach
Z rys. 14.10 dodatkowo wynika, że punkt styczności krzywej obojętności B i krzywej możliwości produkcyjnych wyznacza stosunek cen dóbr, który jest równy obydwóm: MRT i MRS osoby B, jak na rys. 14.9 i w równaniu ![]()
:
![]()
.
Rys. 14.11 pokazuje, że stosunek cen jest również równy MRS osoby A. Wynika z tego, że MRSy są równe dla wszystkich konsumentów oraz, że są one równe stosunkowi cen. Warunek optymalności w sensie Pareta po włączeniu produkcji obejmuje warunki optymalności dystrybucji. Przy alokacji, która jest zarówno efektywna w produkcji, jak i jest optymalna w sensie Pareta, MRSy są równe dla wszystkich konsumentów i jednocześnie równe MRT.
Na rys. 14.11 mapa obojętności B została odwrócona o 1800 czyli jej początek znalazł się w punkcie wyboru optymalnego (x*, y*) tworząc skrzynkę Edgeworth'a dla czystej wymiany o wymiarze x* na y*. Ponieważ ten obrót nie zmienia nachylenia w punkcie styczności, to możemy porównywać nachylenia obu krzywych z MRT.
Wyprowadzenie warunków optymalności w sensie Pareta matematycznie
maxUB(xB, yB)
p.w.: UA(xA, yA) = ![]()
xA + xB = x
yA + yB = y
y = y(x) : krzywa możliwości produkcyjnych
Funkcja Lagrange'a:
![]()
Warunki konieczne:
![]()
![]()
![]()
![]()
![]()
![]()
.
Pamiętając, że MRT = dy/dx:
![]()
Tak więc:
![]()
.
Po uproszczeniu:
![]()
.
Równowaga ogólna w gospodarce doskonale konkurencyjnej
Poziom użyteczności osiągany przez konsumenta oraz realizowana produkcja z krzywej możliwości produkcyjnych zależą od wyposażenia początkowego konsumentów w czynniki. Przyjmujemy, że konsumenci przyjmują ceny jako parametry. Sprzedają więc swe czynniki po cenach rynkowych otrzymując tym sposobem dochody służące zakupowi produktów po cenach rynkowych. Na przykład, jeżeli płaca i cena kapitału wynoszą w oraz r, to konsument A może osiągnąć dochód: MA = wLA + rKA. Przy cenach px oraz py linię ograniczenia budżetowego A opisuje równanie:
pxxA + pyyA = MA = wLA + rKA.
Dla konsumenta B:
pxxB + pyyB = MB = wLB + rKB.
Firma X produkuje xA + xB zatrudniając Kx oraz Lx, a firma Y produkuje yA + yB zatrudniając Ky oraz Ly, gdzie:
KA + KB = Kx + Ky i LA + LB = Lx + Ly .
Równowaga ogólna i równowaga cząstkowa
Graficzne przedstawienie doskonale konkurencyjnej równowagi ogólnej
Przyjmujemy, że w gospodarce jest licytator, podający ceny, które konsumenci i producenci przyjmują jako dane. Proces tatonnement (prób i błędów) trwa aż rynki ulegną oczyszczeniu. Nie można jednoznacznie wyznaczyć cen. Jest tak ponieważ funkcje popytu są homogeniczne stopnia zerowego we wszystkich cenach i dochodzie oraz funkcje popytów pochodnych na czynniki również są homogeniczne stopnia 0 w cenach. Aby przeanalizować proces dochodzenia do równowagi w równowadze ogólnej noramlizujemy jedną z cen (produktu lub czynnika) i wyrażamy inne ceny w postaci stosunku cen względem ceny znormalizowanej. Czyli: ![]()
, ![]()
, ![]()
, ![]()
. To czy te stosunki cen są osiągane w równowadze zależy od popytu konsumentów przy danych stosunkach cen. Aby wyznaczyć popyt określamy dochód każdego z konsumentów przy danym stosunku płacy i ceny kapitału. Następnie piszemy wzór na linię ograniczenia budżetowego każdego konsumenta:
![]()
![]()
.
Konsumenci maksymalizują użyteczność względem powyższych ograniczeń budżetowych. Jeżeli wzdłuż krzywej kontraktowej dla produkcji (xA* + xB*, yA* + yB*) = (x, y), to gospodarka osiąga równowagę przy tych cenach.
Rys. 14.12 przedstawia taką równowagę. Punkty przecięcia linii ograniczenia budżetowego A: ![]()
i ![]()
. Maksymalizuje on swoją użyteczność w (xA*, yA*). Można teraz dołączyć linię ograniczenia budżetowego B do A wykorzystując potencjalne wielkości produkcji w gospodarce. Suma obu linii ograniczenia budżetowego jest styczna do krzywej możliwości produkcyjnych w (X*, Y*), czyli w punkcie styczności krzywej obojętności B. Oznacza to, że w (xA*, yA*) i (xB*, yB*) suma wielkości popytów prowadzących do maksymalizacji użyteczności przez A i B przy tych cenach równa się efektywnej produkcji w gospodarce: xA* + xB*= X* i yA* + yB*= Y*. Gospodarka znajduje się w równowadze.
Ceny czynników i produktów
Wybór punktu (X*, Y*) określa zarówno alokację czynników, jak i cenę pracy w równowadze.
Rys. 14.13 prezentuje to. Punkt (X*, Y*) z krzywej możliwości produkcyjnych jest pokazany jako punkt styczności w skrzynce Edgeworth'a dla produkcji. Zrównanie MRTS wyznacza znormalizowaną stawkę płac, ![]()
. Stosunek między cenami produktów i czynników jest wyznaczony przez zrównanie znormalizowanej płacy ze znormalizowanym przychodem krańcowym z pracy: ![]()
. Aby wszystkie rynki jednocześnie znalazły się w równowadze, znormalizowane ceny muszą zapewnić spełnienie powyższej zależności.
Fundamentalne twierdzenia ekonomii dobrobytu
Z rys. 14.12 wynika, że osiągnięta równowaga spełnia warunki optymalności w sensie Pareta: MRT = MRSy. Zostało to osiągnięte dzięki cenom względnym ![]()
, ![]()
, ![]()
. Tak jak w przypadku czystej wymiany, osiągnęliśmy ważny rezultat, że rynek doskonale konkurencyjny rozwiązuje problemy produkcji i dystrybucji przy wyposażeniach początkowych konsumentów oraz preferencjach i technice spełniających założenia modelu.
Dla produkcji i dystrybucji pierwsze fundamentalne twierdzenie dobrobytu przyjmuje następującą postać. Jeżeli preferencje są: spójne, zwrotne i przechodnie, wykazują się nienasyceniem i malejącymi MRSami i nie ma efektów zewnętrznych w konsumpcji oraz jeżeli produkcję charakteryzuję malejące MRTSy oraz stałe lub malejące korzyści skali a także nie ma efektów zewnętrznych w produkcji (np. zanieczyszczeń), to każda doskonale konkurencyjna równowaga ogólna osiąga efektywność produkcji i jest optymalna w sensie Pareta.
Drugie fundamentalne twierdzenie dobrobytu również rozbudowuje się po uwzględnieniu produkcji oprócz dystrybucji. Każda alokacja z krzywej możliwości produkcyjnych oznacza (impicit) stosunki cen produktów i czynników.
Pokazane jest to na rys. 14.14 dla dwóch różnych punktów. W punkcie A na krzywej możliwości produkcyjnych stosunek cen wynosi px1 / py1 i (x1, y1) jest alokacją doskonale konkurencyjną. Biorąc tę alokację w skrzynce Edgeworh'a stosunek cen czynników wynosi: w1/r1. Analogicznie w punkcie B stosunki cen wynoszą:
px2 / py2 , w2/r2, a alokacja to (x2, y2). Drugie fundamentalne twierdzenie dobrobytu głosi, że przy tych samych założeniach jak do pierwszego twierdzenia, każda alokacja, w której osiągana jest efektywność produkcji i w której potencjalnie może być osiągnięta alokacja optymalna w sensie Pareta, może być doskonale konkurencyjną równowagą ogólną dzięki odpowiedniemu przypisaniu wyposażeń początkowych konsumentom.
Statyka porównawcza w analizie równowagi ogólnej
Pamiętamy, że przy analizie równowagi cząstkowej, krzywa podaży w LR jest doskonale elastyczna, jeżeli ceny czynników nie zmieniają się. Jednocześnie wiadomo, że jeżeli krzywa możliwości produkcyjnych „wybrzusza” się od początku układu współrzędnych, to ceny względne zmieniają się przy wzroście produkcji jednego dobra i zmniejszaniu produkcji drugiego dobra. Zmian gustów na rzecz X oznacza ruch wzdłuż krzywej możliwości produkcyjnych i wzrost produkcji X przy jednoczesnym zmniejszeniu Y. Jest to konieczne dla osiągania efektywności produkcji. Przesunięcie czynników do X oznacza zwiększanie MRT, czyli cena względna X musi w równowadze wzrosnąć względem równowagowej ceny Y. Rys. 14.14. Przy produkcji (x1, y1) ceny względne produktów wynoszą px1 / py1 . Ale w (x2, y2) przy większej produkcji X i mniejszej Y, cena względna wynosi
px2 / py2, czyli jest większa niż px1 / py1.
Jeżeli krzywa kontraktowa dla produkcji jest nieliniowa, to zmiana kombinacji produkcji wzdłuż krzywej możliwości produkcyjnych prowadzi do zmiany cen względnych czynników. Rys. 14.14. Przy wzroście produkcji X z x1 do x2 i zmniejszeniu produkcji Y z y1 do y2 stosunek cen czynników maleje z w1/r1 do w2/r2. Wynika to z faktu, że X jest bardziej kapitałochłonne od Y (wybrzuszenie krzywej kontraktowej). Wzrost produkcji X oznacza więc zwiększenie popytu na kapitał względem popytu na pracę. Przy danym zasobie pracy i kapitału w gospodarce zwiększenie względnego popytu na kapitał zwiększa jego cenę względną i stosunek płacy do ceny kapitału maleje.
Zmiany techniki
Zmiana, która może zmienić ceny względne i która zwiększa osiągalną wielkość produkcji jest zmianą techniki produkcji. Na przykład, neutralna zmiana techniki dotycząca produkcji wszystkich dóbr w tej samej proporcji może nie wpłynąć na ceny względne. Taka zmiana nie wpływa na MRTSy. Co więcej, jeśli dotyczy na wszystkich dóbr proporcjonalnie, to przesunie równolegle PPF bez zmiany MRT.
Rys. 14.15. Jeśli na dodatek preferencje konsumentów są takie, że wszystkie MRS pozostają takie same wzdłuż ścieżki rozwoju (identyczne, jednorodne preferencje), to produkcja obu dóbr zwiększy się, a wszystkie ceny względne nie ulegną zmianie.
Bardziej prawdopodobne jest to, że zmiana techniki doprowadzi do zmiany cen względnych w równowadze ogólnej, jak i wielkości produkcji. Na przykład, przyjmijmy, że neutralna zmiana techniki zwiększająca maksymalną osiągalną wielkość produkcji jednego dobra, ale nie drugiego prowadzi do zmiany kształtu PPF. Nawet przy identycznych jednorodnych preferencjach ceny względne zmienią się. Przy zmianach techniki typu biased lub przy preferencjach, które nie są jednorodne, potencjalne zmiany cen względnych są nawet większe.
Rys. 14.16: zmiana techniki prowadząca do wzrostu produkcji X, ale nie Y. Takie przesunięcie PPF prowadzi do zmniejszenia ceny względnej X przy wzroście produkcji z (x1, y1) do (x2, y2) wzdłuż promienia wychodzącego z początku układu współrzędnych. Ten wynik potwierdza przypuszczenia, że zmiana techniki zmniejszająca koszty produkcji dobra powinna prowadzić do zmniejszenia ceny względnej tego dobra w równowadze ogólnej.