Wyprowadzenie wielomianów

a) metodą Lagrange'a

b) metoda Newtona

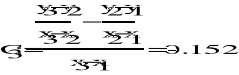
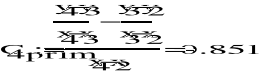
Kod programu

>> x=[0 pi/3 pi/2 3*pi/4];

y=sin(x).^2;

% interpolacje Lagrange'a

[A,L]=lagran(x,y);

w=length(x);

n=w-1;

L=zeros(w,w);

for k=1:n+1

V=1;

for j=1:n+1

if k~=j

V=conv(V,poly(x(j)))/(x(k)-x(j));

end

end

L(k,:)=V;

end

A=y*L;

%interpolacje Newtona

[C,D]=newpoly(x,y);

p=length(x);

D=zeros(p,p);

D(:,1)=y';

for j=2:p

for k=j:p

D(k,j)=(D(k,j-1)-D(k-1,j-1))/(x(k)-x(k-j+1));

end

end

C=D(p,p);

for k=(p-1):-1:1

C=conv(C,poly(x(k)));

m=length(C);

C(m)=C(m)+D(k,k);

end

%obliczenie błędu lokalnego

xlok=pi/4;

Blad=abs(sin(xlok)^2-(A(1)*xlok^3+A(2)*xlok^2+A(3)*xlok+A(4)));

xx=linspace(x(1),x(4),300);

ypom=sin(xx).^2;

yy=polyval(A,xx);

plot(x,y,'ro',xx,ypom,'b-',xx,yy,'k-');

>> x

x =

0 1.0472 1.5708 2.3562

>> y

y =

0 0.7500 1.0000 0.5000

>> A

A =

-0.2967 0.6248 0.3873 0

>> C

C =

-0.2967 0.6248 0.3873 0

>> Blad

Blad =

0.0458

Wykres

Wnioski

Błąd lokalny dla x=pi/4 wyszedł niewielki świadczy to o poprawnym obliczeniu wielomianu interpolacyjnego co również widać na załączonym wyżej wykresie. Z obliczeń widać również, że metoda Lagrange'a oraz Newtona dają takie same wyniki, inna jest tylko metoda obliczeń.