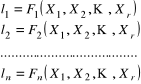
7. Metody mieszane

7.1. Metoda parametryczna z warunkami dla parametrów

W niektórych zadaniach pomiarowych równocześnie występują elementy modelu parametrycznego i warunkowego. Warunki mogą np. dotyczyć współrzędnych punktów sieci, gdy zadane jest ich wzajemne położenie. W takim przypadku poza układem równań obserwacyjnych l_i = F(x):

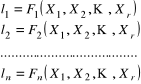
należy utworzyć układ równań warunkowych Ψ(X) = 0 wiążących parametry X₁, X₂,X₃

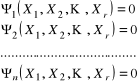
Układ równań
można przekształcić do liniowej postaci równań poprawek

a równania warunkowe
można zastąpić układem równań

Rozwiązanie zadania wyrównawczego polega na rozwiązaniu problemu optymali-zacyjnego przy warunku
sformułowanego układem:

Algorytm rozwiązania zadania wyrównawczego obejmuje wyznaczenie korelat k, poprawek dx oraz poprawek v:

Przykład 7.1. Obliczyć współrzędne narożnika budynku (pkt. 5) znajdującego się w odległości d₅₄ = 182,312m od pkt. 4. Znane są współrzędne punktów 1, 2, 3, 4 w układzie (X,Y) oraz odległości d₅₁ = 151,581 m, d₅₂ = 244,275 m, d₅₃ = 255,235 m.

Tablica 5.1

Punkt	X [m]	Y[m]			Wynik pomiaru	Błąd pomiaru
1	1 400,200	2 389,750		d51	151,581	0,012
2	1 450,080	2 550,150		d52	244,275	0,012
3	1 359,880	2 640,360		d53	255,235	0,005
4	1 219,960	2 589,840

Rys. 7.1

Współrzędne przybliżone punktu 5:

Równania poprawek, budowane na podstawie ogólnego równania (5.11)

Zestawienie macierzy

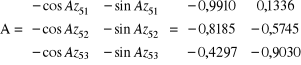
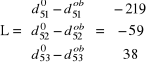
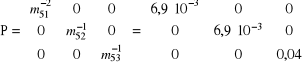
Równanie warunkowe

(postać nieliniowa)

(postać zlinearyzowana) gdzie

Zestawienie macierzy

Obliczenie poprawek

oraz

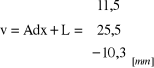
Wyrównane współrzędne punktu Z

Kontrola obliczeń

7.2. Metoda wag

Jeżeli zadanie opisuje układ równań poprawek

v = A·dx + L

oraz warunek

B dv + ၄ = 0

to równanie warunkowe można traktować jako dodatkowe równanie parametryczne o nieskończenie dużej wadze.

Przykład 7.1. Wyznaczyć współrzędne punktu 5 dla zadania jak na rys. 7.2. Dane współrzędne punktów 1, 2, 3 oraz wyniki pomiaru odległości zamieszczono w tablicy 7.2. W zadaniu należy spełnić warunek β = 103.8622.

Tablica 7.2

Punkt	X [m]	Y[m]			Wynik pomiaru	Błąd pomiaru
1	310,055	604,728		d51	171,580	0,008
2	635.417	701,009		d52	210.671	0,015
3	566,200	780, 080		d53	148,235	0,005
4	381,725	834,716		d54	113,609	0,010

Rys. 7.2

Układ równań poprawek rozpisany według ogólnego wzoru (5.11) obejmuje cztery długości oraz równanie dla β.

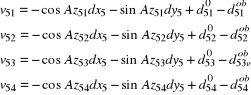
Zestawienie macierzy

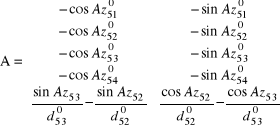
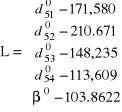
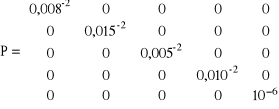
Algorytm rozwiązania zadania jest identyczny jak w metodzie parametrycznej, przykład 5.4.

52

1

4

2

3

51

Ⴐ

Ⴐ

Ⴐ

Ⴐ

Ⴐ

1

2

3

4

5

d₅₂

d₅₁

d₅₄

d₅₃

°

°

°

°

°

β