Sprawozdanie z dendrometrii

Część I Pomiar drzewa leżącego

Ćwiczenie I

Wykonał: Maciej Kiebała Obliczyć miąższość strzały w korze i bez kory wzorami zwykłymi

1. Środkowego przekroju

-w korze

l/2 = 10,785

d_l/2 = 13,14

g_l/2 = 0,0136

V = 0,2925 m³

-bez kory

l/2 = 10,785

d_l/2 = 12,89

g_l/2 = 0,0131

V = 0,2815 m³

2. Smailana

-w korze

l = 21,57

d₀ = 24,5

g₀= 0,0471

V = 0,5084 m³

-bez kory

l = 21,57

d₀ = 22,3

g₀= 0,0391

V = 0,4212 m³

3. Hossfelda

-w korze

l/3 = 7,19

d_l/3 = 15,486

g_l/3 = 0,0188

V = 0,3047 m³

-bez kory

l/3 = 7,19

d_l/3 = 14,286

g_l/3 = 0,0160

V = 0,2593 m³

2. Ocenić dokładność wzorów na drodze empirycznej obliczając: błąd absolutny, błąd procentowy zasadniczy miąższość błąd procentowy wtórny.

Aby móc ocenić doładność wzorów nalezy najpier obliczyc miąższość rzeczywistą a za taką przyjmowana jest miąższość obliczona sekcyjnym wzorem środkowego przekroju. Oto odpowiednie obliczenia:

Należy jeszcze policzyć miąższość ostatniej niepełnej sekcji

a) w korze

d_k = 0,661

g_k = 0,0002

h_k = 0,57

V = 0,000005

b) bez kory

d_k = 0,42

g_k = 0,000015

h_k = 0,57

V = 0,000038

Wiec miąższość całej strzały jest równa odpowiednio

1. w korze - V = 0,323105

2. bez kory - V = 0,26790038

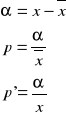
Od razu rzuca się miąższość oczy jak bardzo niedokładny jest wzór Smailana daje on, bowiem olbrzymie błędy. Wynika to miąższość niedopasowanie wzoru do opartego na bryle regularnej do rzeczywistego kształtu strzały. Pozostałe dwa wzory dają pewne błędy jednak są one stosunkowo niewielkie. Najdokładniejszy okazuje się być wzór Hossfelda miąższość to do obliczania miąższości miąższość bez kory.

3. Obliczyć miąższość grubizny strzały wzorem sekcyjnym środkowego przekroju

Należy jeszcze policzyć miąższość ostatniej niepełnej sekcji

a) w korze

Grubość 70 mm wypada na 18,07 m

h = 0,07 m

V = 0,0000003

b) bez kory

Grubość 70 mm wypada na 17,57 m

h = 0,57 m

V = 0,0000165

Wiec miąższość grubizny strzały jest równa odpowiednio:

3. w korze - V = 0,3180003

4. bez kory - V = 0,2599165

---