POLITECHNIKA CZĘSTOCHOWSKA

W CZĘSTOCHOWIE

Instytut Fizyki

Ćwiczenie nr 6

TEMAT: Badanie zależności współczynnika lepkości cieczy od temperatury.

1. Wstęp teoretyczny

1. Mechanizm lepkości.

O lepkości (tarciu wewnętrznym) możemy mówić, gdy ciecz porusza się w pewnym kierunku, przy czym różne jej warstwy poruszają się z różnymi prędkościami. Występują tu dwa rodzaje ruchów: ruch cząsteczkowy oraz ruch poszczególnych warstw płynu.

Współczynnik lepkości cieczy zależy od rodzaju cieczy i wyraża się go wzorem:

;

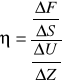
zatem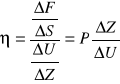

Gdzie: P - ciśnienie sił tarcia wewnętrznego

- jednostkowy spad prędkości (stosunek zmiany prędkości do zmiany odległości warstw ślizgających się)

Jednostką współczynnika lepkości jest 1 niutonosekunda na metr kwadratowy (1N*s/m²).

2. Metody pomiaru współczynnika lepkości.

1. Metoda Stokesa.

Ciecz zwilżająca pokrywa cienką warstwą ciała w niej zanurzone, np. kulkę metalową. Z tego powodu, gdy kulka jest w ruchu, unosi ze sobą warstwę przylegającego płynu, a ten na skutek zjawiska tarcia wewnątrz samego płynu wprawia w ruch następne warstwy (rys. 2.1.1). Z tego powodu siła oporu F_r , z jaką płyn działa na poruszającą się kulkę, zależy od współczynnika lepkości płynu i wyraża się wzorem Stokesa :

F_r=6Πηrv

Jeżeli kulka wykonana jest z materiału o gęstości ρ, większej od gęstości ρ_p płynu, to ruch może następować na skutek działania siły ciężkości F_G=mg=4/3Πr³ρ_kg. Na kulkę działa również siła wyporu F_w=-4/3Πr³ρ_pg. Sumujemy wszystkie siły działające na kulkę

F=F_T+F_g+F_w i mamy

F=4/3Πr³ρ_kg-4/3Πr³ρ_pg-6Πηrv.

Trzeci wyraz prawej strony ostatniego wyrażenia zależy od prędkości i istnieje taka prędkość v₀, przy której siła F jest równa 0, co oznacza, że kulka porusza się ruchem jednostajnym. Jeżeli prędkość jest różna od v₀ , to kulka porusza się ruchem przyspieszonym i jej prędkość rośnie lub maleje do chwili osiągnięcia wartości v₀. Równanie F_r=6Πηrv jest ścisłe tylko wtedy, gdy kulka porusza się w ośrodku o nieograniczonej szerokości i gdy mamy do czynienia z ruchem laminarnym.

Gdy kulka porusza się w rurze o promieniu R wypełnionej cieczą, wtedy równanie Stokesa przyjmuje postać:

F_T=-6Πηrv(1-r/R)^-n

Uwzględniamy tę poprawkę w równaniu F=4/3Πr³ρ_kg-4/3Πr³ρ_pg-6Πηrv i zakładamy F=0 oraz v=l/t, gdzie t - czas spadania kulki na drodze l. Otrzymujemy:

.

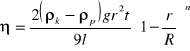
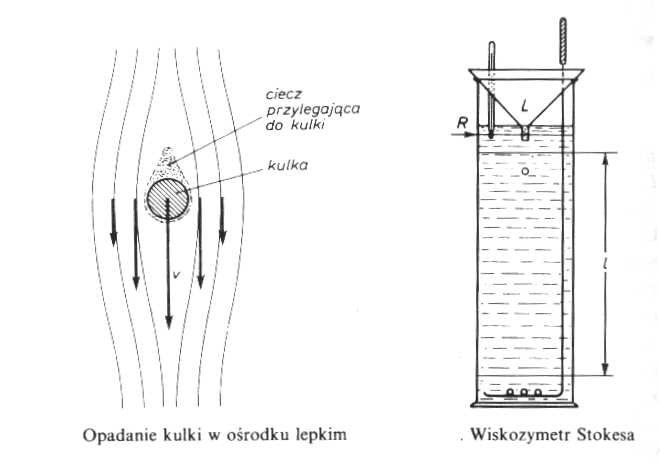
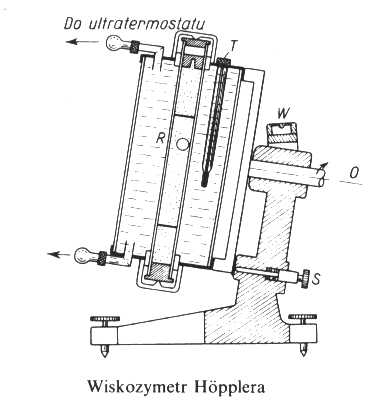
2. Metoda Höpplera

Rurka R, w której mierzymy czas spadku kulki, otoczona jest płaszczem wodnym. Temperaturę wody regulujemy ultratermostatem. Żaden z korków zamykających wodę jest wydrążony i zaopatrzony w wentyl. W temperaturze pokojowej wydrążenie to pozostaje puste. W miarę podgrzewania objętość cieczy rośnie i wydrążenie wypełnia się, a ciśnienie wzrasta tylko nieznacznie. Pomiar czasu spadania kulki można powtarzać wielokrotnie. Wystarczy każdorazowo obrócić przyrząd o kąt Π wokół osi O. Docisk S służy do unieruchomienia rurki, a poziomica W - do kontroli ustawienia przyrządu. Przyrząd zaopatrzony jest w kilka kulek, przeznaczonych do pomiaru cieczy o różnej lepkości, oraz jedną przeznaczoną do pomiaru lepkości gazu. Spadek kulki w płynie zachodzi w rurce o średnicy nieznacznie przekraczającej średnicę kulki. Wtedy rurkę musimy ustawić nieco ukośnie, gdyż przy ustawieniu pionowym ruch kulki nie jest jednostajny. Przy ustawieniu skośnym kulka toczy się po ścianie rurki. Do omawianego przypadku stosuje się również wzór:

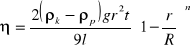
zapisany w postaci η=K(ρ_k-ρ_p)t, gdzie K jest stałą przyrządu, którą wyznaczamy z pomiaru wykonanego dla płynu o znanym współczynniku lepkości. Poprawne wyniki pomiarów uzyskuje się tylko wtedy, gdy przyrząd jest bardzo czysty. Stąd przed pomiarem należy wnętrze rurki R oraz kulkę dokładnie oczyścić i przemyć alkoholem lub eterem.

Ciecz przeznaczoną do pomiaru należy wygotować, by w ten sposób pozbawić ją resztek gazów zakłócających pomiary. Przed rozpoczęciem pomiarów wygotowaną ciecz ochładzamy do temperatury pokojowej, po czym wypełniamy rurkę wiskozymetru. Usunąć musimy pęcherzyki powietrza, które pozostały na ściankach. Wkładamy kulkę i zamykamy korkiem, zwracając uwagę na to, by wydrążenie w korku nie było całkowicie wypełnione cieczą. Czas spadku kulki mierzymy sekundomierzem. Dokładną wartość temperatury odczytujemy na termometrze T znajdującym się w wiskozymetrze.

3. Definicja współczynnika lepkości cieczy.

Współczynnik lepkości jest wielkością fizyczną charakteryzującą ośrodki fizyczne (ciecz lub gaz) pod względem tarcia wewnętrznego. Współczynnik lepkości, czyli napięcie styczne powoduje jednostkowy spadek prędkości.

II. Tabela wyników i wykresy.

Lp.	k [m^2/s^2]	d1 [kg/m^3]	d2 [kg/m^3]	T [^oC]	t [s]	η [N*s/m^2]
1 2 3 4 5 6 7	1,184* 10^-6	8,12*10^3	1,26*10^3	26 31 35,5 41 47 51 55,5	131,4 87,6 59,8 51 42 37 30	1,067 0,711 0,485 0,414 0,341 0,3 0,243

1 - z obliczeń

2 - z pomiarów

III. Obliczenia.

Kształt krzywej z wykresu wykazuje przebieg wykładniczy zgodnie z zależnością:

gdzie A i B - stałe materiałowe charakteryzujące daną ciecz, T - temperatura w skali Kelvina.

Stałe te można wyznaczyć na podstawie zebranego w ćwiczeniu materiału doświadczalnego w następujący sposób:

Piszemy równania krzywej dla dwóch różnych temperatur:

Logarytmujemy oba równania:

Po rozwiązaniu tego układu równań otrzymujemy wzory na stałe A i B:

Po podstawieniu:

T₁ = 26 [^OC] = 299,16 [K] η₁ = 1,067 [N*s/m²]

T₂ = 55,5 [^OC] = 328,66 [K] η₂ = 0,243 [N*s/m²]

otrzymujemy:

Po podstawieniu do równania krzywej:

otrzymujemy dla poszczególnych temperatur:

T₁=299,16[K] η₁=1,07[N*s/m²]

T₂=304,16[K] η₂=0,816[N*s/m²]

T₃=308,66 [K] η₃=0,644[N*s/m²]

T₄=314,16 [K] η₄=0,487[N*s/m²]

T₅=320,16[K] η₅=0,362[N*s/m²]

T₆=324,16[K] η₆=0,3[N*s/m²]

T₇=328,66[K] η₇=0,243[N*s/m²]

IV.Wnioski.

Z zależności = (T) wynika, że wraz ze wzrostem temperatury badanej cieczy jej współczynnik lepkości maleje nieliniowo. Niedokładności pomiaru współczynnika lepkości wynikają z mało precyzyjnego pomiaru czasu opadania kulki. Pod wpływam temperatury siły oddziaływania między cząsteczkami badanej cieczy maleją, a także maleją siły oddziaływania między kulką a cieczą. W związku z tym maleje współczynnik lepkości, który charakteryzuje opór cieczy podczas płynięcia wywołanego siłami zewnętrznymi.

Błąd pomiaru współczynnika lepkości

Jako błąd odczytu czasu przyjąłem tu wartość t=1,2s wynikającą z podziałki stopera. Ponadto należy uwzględnić błędy przy pomiarze czasu związane z bezwładnością oka ludzkiego (moment przekraczania przez kulkę poziomów). W związku z tym całkowity błąd przy wyznaczaniu współczynnika lepkości można przyjąć jako = 0,009.

Na podstawie obliczeń z zależności

wyznaczyliśmy krzywą teoretyczną η=f(T), której przebieg jest nieco odchylony od tej uzyskanej w wyniku pomiarów. Obie krzywe przecinają się ze sobą dla temperatur 299,16 [K]

i 328,66 [K], wykorzystanych do wyznaczenia stałych materiałowych A i B. W celu uzyskania najdokładniejszych wyników wzięliśmy pod uwagę dwie skrajne temperatury, dla których zostały przeprowadzone pomiary.

1

---