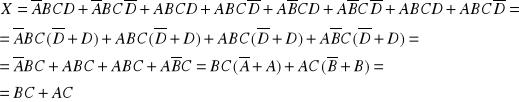
Sprawozdanie

Ćwiczenie nr 4-układy logiczne

Grupa IEPS zespół G

Bartoszuk Piotr

Ćwiek Kamil

Gajewski Cezary

Wieczorek Michał

Na laboratorium naszym zadaniem było badanie układów logicznych, „czarnej skrzynki” która realizowała funkcję logiczną której syntezę mieliśmy przeprowadzić, oraz licznik rewersyjny złożony z przerzutników typu T oraz bramek logicznych typu NOR.

1.Badanie „czrnej skrzynki”

Wprowadzając na wejścia układu sygnały logiczne 0 i 1 zapisywaliśmy wartości funkcji XiY. Wyniki zapisane w postaci tabeli w protokole należy przedstawić w postaci tablic Karnaugh, aby przeprowadzić syntezę funkcji:

Funkcja X:

	00	01	11	10
00	0	0	0	0
01	0	0	1	1
11	0	0	1	1
10	0	0	1	1

Jedynki występujące w tej tablicy można skleić w dwie „czwórki”, synteza funkcji X z wykorzystaniem praw algebry Boole`a wygląda więc następująco:

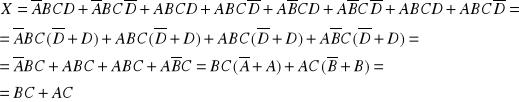
Aby zrealizować tę funkcję za pomocą bramek NOR wykonujących funkcję
, należy wykorzystać prawa de Morgana:

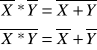
Przekształcenie funkcji X:

Schemat układu logicznego zbudowanego z bramek NOR:

Układ ten zrealizowaliśmy na laboratorium, otrzymana funkcja była taka sama jak funkcja „czarnej skrzynki”

Funkcja Y:

	00	01	11	10
00	0	0	0	0
01	0	1	1	0
11	1	1	1	1
10	1	1	1	1

Jedynki w tej tablicy można „skleić” jako jedna „ósemka” i „jedna czwórka”

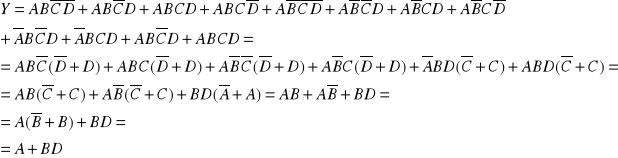
Stosując prawa de Morgana można tę funkcję przekształcić do postaci:

Układ realizujący funkcję Y stworzony z bramek logicznych NOR:

Układ ten po przebadaniu na stanowisku laboratoryjnym spełniał takie same funkcje jak funkcja Y „czarnej skrzynki”

2.Badanie licznika

W tej części ćwiczenia mieliśmy za zadanie zaprojektować układ licznika rewersyjnego składającego się z dwóch przerzutników typu T, który realizował by zliczanie w obu kierunkach bez konieczności ręcznego przełączania wejścia przerzutnika drugiego między wyjściami pierwszego. Schemat licznika zasadniczego:

Zasada działania tego licznika opiera się na tabeli prawdy przerzutnika T który przy pojawieniu się na wejściu wartości logicznej 1 zmienia stan swoich wyjść na przeciwne(licznik wyzwalany jest zboczem ujemnym sygnału).W ten sposób badając stan jednego z wyjść kolejnych przerzutników uzyskuje się efekt liczenia w systemie binarnym co można przeliczyć na system dziesiętny przyjmując że każde wyjście jest kolejną potęgą liczby 2.Przedstawiony powyżej licznik może więc liczyć do 4 gdyż wyjścia jego przerzutników będą przedstawiały

i ma on następujące stany :

Q1	Q2	Nr stanu
1	0	1
0	1	2
1	1	3
0	0	4

Przy zmianie przyłączenia wejścia przerzutnika 2 z Q`1 do Q1 licznik zliczał by w kierunku przeciwnym.

Schemat zaprojektowanego licznika rewersyjnego jest następujący:

Licznik ten przy przełączaniu przełącznika „+-” realizował funkcję zliczania w dwóch kierunkach. U podstawy jego działania leży tabela prawdy bramek NOR które na wyjściu podają stan wysoki tylko jeśli na obu wejściach występuje stan logiczny niski. W ten sposób jedno z wyjść przerzutnika pierwszego jest odłączone( zależnie od przełącznika +-) od wejścia przerzutnika drugiego przez co licznik działa tak jak licznik jednokierunkowy, po przełączeniu „+-” , z wejściem przerzutnika 2 współpracuje drugie wyjście przerzutnika 1 przez co licznik zaczyna zliczać w drugim kierunku, jest więc to licznik rewersyjny.

2b.Układ kontroli licznika rewersyjnego

W punkcie tym należało skonstruować układ kontroli licznika który sygnalizuje zliczenie kolejnego impulsu poprzez zapalenie jednej z czterech żarówek(żarówka świeci gdy na jej wejściu pojawia się stan logiczny wysoki), przy czym żadne z zarówek nie mogą świecić jednocześnie , tak więc każda z żarówek reprezentuje jedną cyfrę od 1 do 4.Układu tego nie dało by się zrealizować bez wykorzystania bramek logicznych gdyż wyjścia przerzutników mają tylko dwa stany, 0 i 1 przez co jednocześnie działać w tym systemie mogły by tylko dwie żarówki a więc sygnalizowane byłoby liczenie do dwóch. Układ wykorzystuje więc bramki NOR na których wyjściu pojawia się 1 tylko wtedy gdy na wejściach są 0.Mając do dyspozycji cztery wyjścia przerzutników licznika, z których zawsze dwa są w stanie niskim a dwa w stanie wysokim należy tak połączyć układ z czterema bramkami NOR aby w kolejnych stanach licznika tylko na jednej bramce występowały dwa stany niskie, mechanizm ten przedstawia tabela:

Q1		Q2		Wejścia bramek NOR	Stany logiczne kolejnych żarówek
0	1	0	1		1000
0	1	1	0		0100
1	0	0	1		0010
1	0	1	0		0001

Schemat układu:

Powyższy układ realizował na ćwiczeniu swoje zadanie.

Wnioski:

Dzięki tablicom Karnaugh synteza funkcji logicznych jest możliwa do zrealizowania w krótkim czasie, prawa de Morgana pozwalają każdą funkcję logiczna zrealizować za pomocą bramek NOR(negacji sumy logicznej) pozwala to na ograniczenie różnorodności elementów wchodzących w skład układu logicznego. Bramki NOR umożliwiły także zrealizowanie licznika rewersyjnego oraz układu jego kontroli. Układ kontroli licznika jest w praktyce urządzeniem bardzo przydatnym gdyż pozwala jednym „rzutem oka” poznać stan licznika, wyręcza nas z konieczności poznawania numeru impulsu na podstawie stanów wyjść przerzutników wchodzących w skład licznika.

---