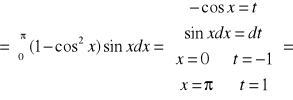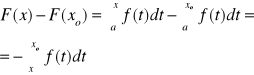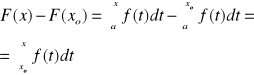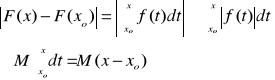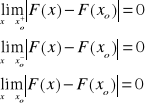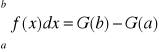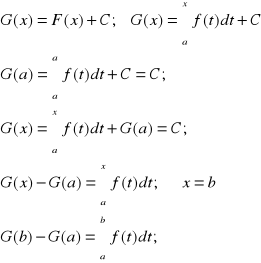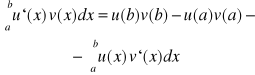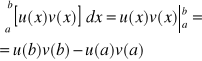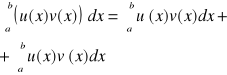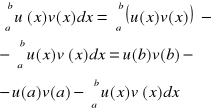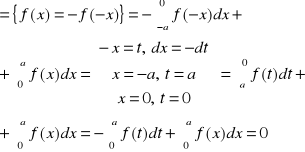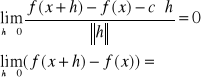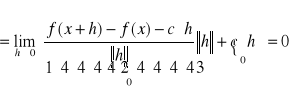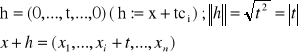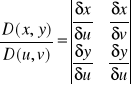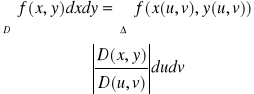Twierdzenia + Dowody 9. Całkowanie przez podstawienie całek oznaczonych. Przykład. Zachodzi wzór : Założenia: - funkcja g ma w przedziale [α,β] ciągłe pochodne, - funkcja f jest ciągła w zbiorze g([α,β]), - g(α) = a , g (β) = b Dowód. F - fun. pierw f	Przykład.	16. Liniowość całki oznaczonej. Jeśli , to: Dowód: a = x o < x1 < ... < xn = b Tworzę sumę całkową dla αf(x) βg(x) : stąd : powyższa liczba nie zależy od doboru punktów Ci i ciągu Δn. Stąd zachodzi udowadniany wzór.	17.Całkowanie iloczynu dwóch funkcji całkowalnych. Jeżeli Dowód: 18. Gdy f ≤ gcałki oznaczone funkcji f ,g.	20. Twierdzenie o wartości średniej całek oznaczonych. Jeżeli f : [a,b] →R jest ciągła, to istnieje takie c ∈ [a,b] że: Dowód. Z tw. Weierstrassa istnieje m,M takie że m ≤ f(x) ≤ M w [a,b], stąd: Z ciągłości f przyjmuję wszystkie wartości pośrednie pomiędzy m a M. Jedną z nich jest średnia całkowa. Stąd:	21. Nierówność pomiędzy całkami (moduły). Jeżeli f całkowalna w sens. Reim. to : Dowód:
22. Podstawowe tw. rachunku całkowego. Niech . Funkcja górnej granicy całkowania: Jeżeli f jest całkowalna to funkcja górn. gran. całkow. F jest ciągła i ma pochodne w każdym punkcie x ∈ [a,b] w którym funkcja f jest ciągła. Ponadto w każdym punkcie przedziału zachodzi związek F`(x) = f(x). Dowód: I. Ciągłośc xo ∈ [a,b] , x < x0	Gdzie M jest pewnym dodatnim ograniczeniem górnym f tj. | f(x) | ≤ M , x ∈ [a,b]. Istnienie M jest rezultatem całkowalności funkcji f, (f całkowal. są ograniczone) oznacza to: x > x0 Również:	II. Różniczkowalność. Zakładam, że f jest ciągła w przedziale x ∈ [a,b] Z tw. o wartości średniej dla całek istnieje taki punkt cn ∈[x, x+h] że: 23. Wzór Newtona - Leibniza. Jeżeli funkcja f:[a,b]→R jest ciągła, to : Dla dowolnej G pierwotnej dla f. dowód→	Dowód: G - pierwotna dla f tj. G`(x) = f(x) F - pierwotna dla f tj. F`(x)=f(x) stąd:	24. Całkowanie przez części całki oznaczonej. Jeżeli funkcje u , v : [a,b]→R mają ciągłe pochodne, to : Dowód:
25. Twierdzenie o całkach funkcji parzystych i nieparzystych. f : R→R jest parzysta gdy f (-x) = f (x) a nieparzysta gdy f (-x) = - f(x). Jeżeli a > 0 oraz funkcja f: [-a,a] →R jest ciągła to: a) jeżeli f jest nieparzysta b) jeżeli f jest parzysta Dowód:	II. Funkcji wielu zmiennych. 23. TW. o ciągłości funkcji różniczkowalnej n zmiennych. TW. U ⊂ R^n jest zbiorem otwartym; x ∈ U; Jeżeli funkcja f : U→R jest różniczkowalna w punkcie x, to jest ciągła w tym punkcie. Dowód: Należy sprawdzić czy: Z definicji różniczkowalności istnieje wektor c ∈ R^n taki,że:	24. TW. o istnieniu pochodnych cząstkowych f n. TW. U ⊂ R^n jest zbiorem otwartym; x = (x1,x2,...,xn) ∈ U; f : U→R. Jeżeli funkcja f jest różniczkowalna w punkcie x, to ma w tym punkcie pochodną cząstkową względem każdej zmiennej. Dowód: Z różniczkowalności istnieje wektor c=(c1,c2,...,cn) taki, że: h=(0,..., t,...,0) ( h:=x+tci) ze wzoru (*)	25. WK istnienia extremum lokalnego. Zakładam f: U→R, U ⊂ R^n jest zbiorem otwartym, funkcja f ma w zbiorze U pochodne cząstkowe. Jeżeli funkcja f ma w pkt. a ∈ U extremum lokalne, to:	9.Zamiana zmiennych w całce podwójnej. Niech przekształcenie 1) x = x (u,v), y = y (u,v) odwzorowuje obszar regularny domknięty Δ w płaszczy. u i v na obszar regularny domknięty D w płaszczy. x i y. Jeżeli funkcje x,y są klasy C^1 to wyrażenie : nazywamy jakobianem przekształcenia 1). Jeżeli w przekształceniu 1): - funkcje x(u,v), y(u,v) są klasy C^1 w pewnym zbiorze otwartym U zawierającym obszar regularny Δ, - D - obszar regularny - Wnętrze obszaru Δ przechodzi w przekształcenie x = x (u,v), y = y (u,v) na wnętrze obszaru D, - Jakobian różny od zera dla każdych (u,v) ∈ U - f(x,y) jest ciągła w D to zachodzi wzór:	10. Zamiana zmiennych na biegunowe. Założenia punktu9. x = ρcosϕ, y = ρsinϕ, mamy: 8. Własności całek podwójnych. Założenia: D1,D2,D - obszary normalne. - - jeżeli D1 D2 nie mają wspólnych pkt. wewnętrznych, to:

---