Zestaw 1
Sformułuj tw Laplace'a (o macierzy kofaktorów)
Podaj definicję odwzorowania liniowego.
W standardowej interpretacji geometrycznej {z ∈ C :
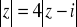
} jest to okrąg o promieniu ….Niech
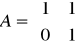
oraz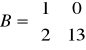
. Wskazać (lub stwierdzić, że nie istnieje) wymierną macierz X spełniającą równanie: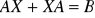
.Niech (Q-endomorfizm) α : Q2×2 → Q2×2 dany będzie wzorem: α(X) = X + 3Xt. Wówczas: det α = ………… oraz tr α = ……..
Niech (Q-liniowe) odwzorowanie α ma w pewnych ubazach macierz:
Sformułować tw Kronecker'a-Capelli (o rozwiązalności)
Niech ubazy B, C, S w R2 dane będą przez: B =
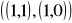
oraz C =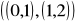
oraz S =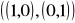
. Niech α : R2 → R2 będzie liniowe takie, że mCB(α) =
(przypomnienie: notacja oznacza, że B jest ubazą w dziedzinie…).Niech (wymierna macierz)
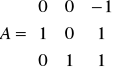
. Niech B = A57. Wówczas B33 = ….Niech (zespolona macierz)
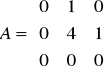
. Wypisz wielomian minimalny, ciąg niezmienników wielomianowych (wielomiany zmiennej x) oraz jakąś (dolną) postać Jordana macierzy A.Sformułuj tw Cauchy'ego (o wyznaczniku iloczynu)
Podaj definicję przestrzeni ortogonalnej (do zbioru w przestrzeni z iloczynem skalarnym).
W standardowej interpretacji geometrycznej {z ∈ C :
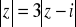
} jest to okrąg o promieniu ….Niech
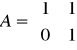
oraz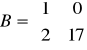
. Wskazać (lub stwierdzić, że nie istnieje) wymierną macierz X spełniającą równanie: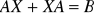
.Niech (Q-endomorfizm) α : Q2×2 → Q2×2 dany będzie wzorem: α(X) = X + 2Xt. Wówczas: det α = ………… oraz tr α = ……..
Niech (Q-liniowe) odwzorowanie α ma w pewnych ubazach macierz:
Sformułować tw Kronecker'a-Capelli (o rozwiązalności)
Niech ubazy B, C, S w R2 dane będą przez: B =
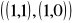
oraz C =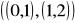
oraz S =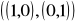
. Niech α : R2 → R2 będzie liniowe takie, że mCB(α) =
(przypomnienie: notacja oznacza, że B jest ubazą w dziedzinie…).Niech (wymierna macierz)
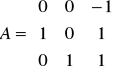
. Niech B = A85. Wówczas B33 = ….Niech (zespolona macierz)
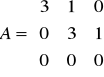
. Wypisz wielomian minimalny, ciąg niezmienników wielomianowych (wielomiany zmiennej x) oraz jakąś (dolną) postać Jordana macierzy A.Podaj jaki jest związek między wymiarami jądra i obrazu odwzorowania liniowego.
Podaj definicję wielomianu minimalnego (macierzy).
W standardowej interpretacji geometrycznej {z ∈ C :
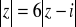
} jest to okrąg o promieniu ….Niech
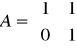
oraz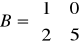
. Wskazać (lub stwierdzić, że nie istnieje) wymierną macierz X spełniającą równanie: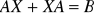
.Niech (Q-endomorfizm) α : Q2×2 → Q2×2 dany będzie wzorem: α(X) = X + 5Xt. Wówczas: det α = ………… oraz tr α = ……..
Niech (Q-liniowe) odwzorowanie α ma w pewnych ubazach macierz:
Sformułować tw Kronecker'a-Capelli (o rozwiązalności)
Niech ubazy B, C, S w R2 dane będą przez: B =
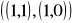
oraz C =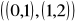
oraz S =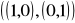
. Niech α : R2 → R2 będzie liniowe takie, że mCB(α) =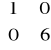
(przypomnienie: notacja oznacza, że B jest ubazą w dziedzinie…).Niech (wymierna macierz)
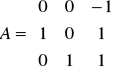
. Niech B = A75. Wówczas B33 = ….Niech (zespolona macierz)
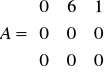
. Wypisz wielomian minimalny, ciąg niezmienników wielomianowych (wielomiany zmiennej x) oraz jakąś (dolną) postać Jordana macierzy A.Sformułuj tw Hamilton'a - Cayley'a (o wielomianie charakterystycznym)
Podaj definicję podprzestrzeni wektorowej (pewnej przestrzeni wektorowej).
W standardowej interpretacji geometrycznej {z ∈ C :
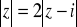
} jest to okrąg o promieniu ….Niech
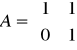
oraz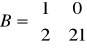
. Wskazać (lub stwierdzić, że nie istnieje) wymierną macierz X spełniającą równanie: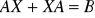
.Niech (Q-endomorfizm) α : Q2×2 → Q2×2 dany będzie wzorem: α(X) = X + Xt. Wówczas: det α = ………… oraz tr α = ……..
Niech (Q-liniowe) odwzorowanie α ma w pewnych ubazach macierz:
Sformułować tw Kronecker'a-Capelli (o rozwiązalności)
Niech ubazy B, C, S w R2 dane będą przez: B =
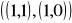
oraz C =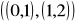
oraz S =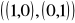
. Niech α : R2 → R2 będzie liniowe takie, że mCB(α) =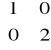
(przypomnienie: notacja oznacza, że B jest ubazą w dziedzinie…).Niech (wymierna macierz)
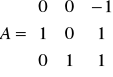
. Niech B = A91. Wówczas B33 = ….Niech (zespolona macierz)
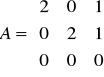
. Wypisz wielomian minimalny, ciąg niezmienników wielomianowych (wielomiany zmiennej x) oraz jakąś (dolną) postać Jordana macierzy A.
|
Niech ![]()
będzie taka, że det A = 2. Niech c(A) oznacza macierz kofaktorów A. Wówczas det c(A) = …..
|
Odwzorowanie α: R → R dane przez α(x) = 2x + 1 nie jest (R) liniowe bowiem
………………………………………………………………………
Odp: Istnieje? (T/N) X = …..
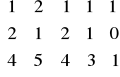
Wówczas: dim ker α = …………. oraz dim im α = ……….
|
Czy (wymierny) układ równań którego macierzą rozszerzoną jest macierz z zadania 6 jest niesprzeczny? Odp: (T/N) ……. . Jeśli jest niesprzeczny to podać też wymiar jego zbioru rozwiązań. Odp: dim = ……..
Wówczas: mSS(α) = ……..
Odp:
mA = ……………………
iA = ……………………..
pJord = ………………….
Zestaw 2
|
Niech ![]()
będą takie, że det A = 2 oraz det B = 3.
Wówczas det (-2A-1B) = …..
|
Wskaż niezerowy wektor o współczynnikach całkowitych ortogonalny do
span{(1, 2, 3), (1, 3, 1)} w R3 (standardowy il skal.). Odp: …………….
Odp: Istnieje? (T/N) X = …..

Wówczas: dim ker α = …………. oraz dim im α = ……….
|
Czy (wymierny) układ równań którego macierzą rozszerzoną jest macierz z zadania 6 jest niesprzeczny? Odp: (T/N) ……. . Jeśli jest niesprzeczny to podać też wymiar jego zbioru rozwiązań. Odp: dim = ……..
Wówczas: mSS(α) = ……..
Odp:
mA = ……………………
iA = ……………………..
pJord = ………………….
Zestaw 3
|
Niech odwzorowanie liniowe α : Q7 → Q5 będzie takie, że dim ker α = 3.
Wówczas dim im α = …..
|
Niech (Q macierz) A = diag(1, 2, 1). Wówczas mA(x) = …………….
Odp: Istnieje? (T/N) X = …..

Wówczas: dim ker α = …………. oraz dim im α = ……….
|
Czy (wymierny) układ równań którego macierzą rozszerzoną jest macierz z zadania 6 jest niesprzeczny? Odp: (T/N) ……. . Jeśli jest niesprzeczny to podać też wymiar jego zbioru rozwiązań. Odp: dim = ……..
Wówczas: mSS(α) = ……..
Odp:
mA = ……………………
iA = ……………………..
pJord = ………………….
Zestaw 4
|
Niech ![]()
będzie taka, że chA(x) = x3 + x - 1. Wskazać wielomian w ∈ Q[x] taki, że deg w ≤ 2 oraz w(A) = A-1. Odp: w(x) = …..
|
Niech L = {(x, y)∈R3: x + y = 3}. Zbiór L nie jest podprzestrzenią wektorową R2 bowiem ………………………………………………………………………
Odp: Istnieje? (T/N) X = …..

Wówczas: dim ker α = …………. oraz dim im α = ……….
|
Czy (wymierny) układ równań którego macierzą rozszerzoną jest macierz z zadania 6 jest niesprzeczny? Odp: (T/N) ……. . Jeśli jest niesprzeczny to podać też wymiar jego zbioru rozwiązań. Odp: dim = ……..
Wówczas: mSS(α) = ……..
Odp:
mA = ……………………
iA = ……………………..
pJord = ………………….
8
Wyszukiwarka
Podobne podstrony:
Baza pytań egzaminacyjnych, FiR UG, Informatyka TI (Marek Markowski)
Algebra liniowa 1 kolokwia i egzaminy Gewert Skoczylas
Algebra liniowa 1 kolokwia i egzaminy Gewert Skoczylas
inf, SGGW, Niezbędnik Huberta, Leśnictwo, Semestr 1, Technologia Informacyjna, Egzamin
Informacja dotycząca egzaminu, Semestr IV, PPUE
Informatyka pytania na egzamin semestr III, spis alfabetyczny
Inżynieria oprogramowania Przykładowe pytania na egzamin 4 semestr, edukacja i nauka, Informatyka
kilka pytan z egzaminu 2010 INFA, Studia WZR zarządzanie 2013-2014, semestr I, Technologia Informacy
pytania z egzaminu pORTFEL iNWESTYCYJNY PROF OSTROWSKA RÓŻNE LATA 2012-2015, Semestr 2 UG, Portfel I
inf-sciaga, SGGW, Niezbędnik Huberta, Leśnictwo, Semestr 1, Technologia Informacyjna, Egzamin
Egzamin ANA1 04092000, Informatyka i Ekonometria SGGW, Semestr 1, Analiza Matematyczna, materialy od
Zagadnienia do egzaminu z przedmiotu grafika komputerowa na semestr I, technik informatyk, soisk utk
Zagadnienia egzaminacyjne z Informatyki, STUDIA SGGW Wydział Leśny leśnictwo, Semestr 1 i 2, Technol
IP EGZAMIN, Studia PŚK informatyka, Semestr 5, Inżunieria programowania, Egzamin
więcej podobnych podstron