Sformułuj tw Laplace'a (o macierzy kofaktorów)
|
Niech ![]()
będzie taka, że det A = 2. Niech c(A) oznacza macierz kofaktorów A. Wówczas det c(A) = …..
Podaj definicję odwzorowania liniowego.
W standardowej interpretacji geometrycznej {z ∈ C :
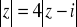
} jest to okrąg o promieniu ….Niech
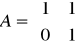
oraz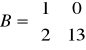
. Wskazać (lub stwierdzić, że nie istnieje) wymierną macierz X spełniającą równanie: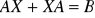
.Niech (Q-endomorfizm) α : Q2×2 → Q2×2 dany będzie wzorem: α(X) = X + 3Xt. Wówczas: det α = ………… oraz tr α = ……..
Niech (Q-liniowe) odwzorowanie α ma w pewnych ubazach macierz:
Sformułować tw Kronecker'a-Capelli (o rozwiązalności)
Niech ubazy B, C, S w R2 dane będą przez: B =
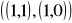
oraz C =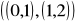
oraz S =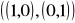
. Niech α : R2 → R2 będzie liniowe takie, że mCB(α) =
(przypomnienie: notacja oznacza, że B jest ubazą w dziedzinie…).Niech (wymierna macierz)
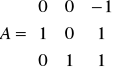
. Niech B = A57. Wówczas B33 = ….Niech (zespolona macierz)
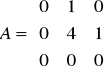
. Wypisz wielomian minimalny, ciąg niezmienników wielomianowych (wielomiany zmiennej x) oraz jakąś (dolną) postać Jordana macierzy A.Sformułuj tw Cauchy'ego (o wyznaczniku iloczynu)
Podaj definicję przestrzeni ortogonalnej (do zbioru w przestrzeni z iloczynem skalarnym).
W standardowej interpretacji geometrycznej {z ∈ C :
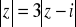
} jest to okrąg o promieniu ….Niech
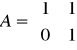
oraz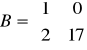
. Wskazać (lub stwierdzić, że nie istnieje) wymierną macierz X spełniającą równanie: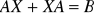
.Niech (Q-endomorfizm) α : Q2×2 → Q2×2 dany będzie wzorem: α(X) = X + 2Xt. Wówczas: det α = ………… oraz tr α = ……..
Niech (Q-liniowe) odwzorowanie α ma w pewnych ubazach macierz:
Sformułować tw Kronecker'a-Capelli (o rozwiązalności)
Niech ubazy B, C, S w R2 dane będą przez: B =
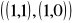
oraz C =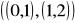
oraz S =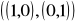
. Niech α : R2 → R2 będzie liniowe takie, że mCB(α) =
(przypomnienie: notacja oznacza, że B jest ubazą w dziedzinie…).Niech (wymierna macierz)
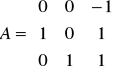
. Niech B = A85. Wówczas B33 = ….Niech (zespolona macierz)
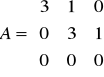
. Wypisz wielomian minimalny, ciąg niezmienników wielomianowych (wielomiany zmiennej x) oraz jakąś (dolną) postać Jordana macierzy A.Podaj jaki jest związek między wymiarami jądra i obrazu odwzorowania liniowego.
Podaj definicję wielomianu minimalnego (macierzy).
W standardowej interpretacji geometrycznej {z ∈ C :
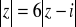
} jest to okrąg o promieniu ….Niech
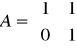
oraz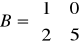
. Wskazać (lub stwierdzić, że nie istnieje) wymierną macierz X spełniającą równanie: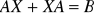
.Niech (Q-endomorfizm) α : Q2×2 → Q2×2 dany będzie wzorem: α(X) = X + 5Xt. Wówczas: det α = ………… oraz tr α = ……..
Niech (Q-liniowe) odwzorowanie α ma w pewnych ubazach macierz:
Sformułować tw Kronecker'a-Capelli (o rozwiązalności)
Niech ubazy B, C, S w R2 dane będą przez: B =
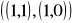
oraz C =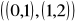
oraz S =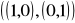
. Niech α : R2 → R2 będzie liniowe takie, że mCB(α) =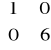
(przypomnienie: notacja oznacza, że B jest ubazą w dziedzinie…).Niech (wymierna macierz)
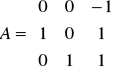
. Niech B = A75. Wówczas B33 = ….Niech (zespolona macierz)
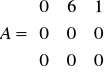
. Wypisz wielomian minimalny, ciąg niezmienników wielomianowych (wielomiany zmiennej x) oraz jakąś (dolną) postać Jordana macierzy A.Sformułuj tw Hamilton'a - Cayley'a (o wielomianie charakterystycznym)
Podaj definicję podprzestrzeni wektorowej (pewnej przestrzeni wektorowej).
W standardowej interpretacji geometrycznej {z ∈ C :
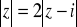
} jest to okrąg o promieniu ….Niech
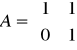
oraz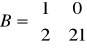
. Wskazać (lub stwierdzić, że nie istnieje) wymierną macierz X spełniającą równanie: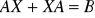
.Niech (Q-endomorfizm) α : Q2×2 → Q2×2 dany będzie wzorem: α(X) = X + Xt. Wówczas: det α = ………… oraz tr α = ……..
Niech (Q-liniowe) odwzorowanie α ma w pewnych ubazach macierz:
Sformułować tw Kronecker'a-Capelli (o rozwiązalności)
Niech ubazy B, C, S w R2 dane będą przez: B =
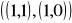
oraz C =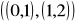
oraz S =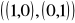
. Niech α : R2 → R2 będzie liniowe takie, że mCB(α) =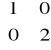
(przypomnienie: notacja oznacza, że B jest ubazą w dziedzinie…).Niech (wymierna macierz)
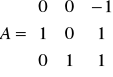
. Niech B = A91. Wówczas B33 = ….Niech (zespolona macierz)
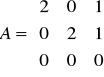
. Wypisz wielomian minimalny, ciąg niezmienników wielomianowych (wielomiany zmiennej x) oraz jakąś (dolną) postać Jordana macierzy A.
|
Odwzorowanie α: R → R dane przez α(x) = 2x + 1 nie jest (R) liniowe bowiem
………………………………………………………………………
Odp: Istnieje? (T/N) X = …..
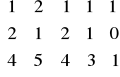
Wówczas: dim ker α = …………. oraz dim im α = ……….
|
Czy (wymierny) układ równań którego macierzą rozszerzoną jest macierz z zadania 6 jest niesprzeczny? Odp: (T/N) ……. . Jeśli jest niesprzeczny to podać też wymiar jego zbioru rozwiązań. Odp: dim = ……..
Wówczas: mSS(α) = ……..
Odp:
mA = ……………………
iA = ……………………..
pJord = ………………….
Zestaw 2
|
Niech ![]()
będą takie, że det A = 2 oraz det B = 3.
Wówczas det (-2A-1B) = …..
|
Wskaż niezerowy wektor o współczynnikach całkowitych ortogonalny do
span{(1, 2, 3), (1, 3, 1)} w R3 (standardowy il skal.). Odp: …………….
Odp: Istnieje? (T/N) X = …..

Wówczas: dim ker α = …………. oraz dim im α = ……….
|
Czy (wymierny) układ równań którego macierzą rozszerzoną jest macierz z zadania 6 jest niesprzeczny? Odp: (T/N) ……. . Jeśli jest niesprzeczny to podać też wymiar jego zbioru rozwiązań. Odp: dim = ……..
Wówczas: mSS(α) = ……..
Odp:
mA = ……………………
iA = ……………………..
pJord = ………………….
Zestaw 3
|
Niech odwzorowanie liniowe α : Q7 → Q5 będzie takie, że dim ker α = 3.
Wówczas dim im α = …..
|
Niech (Q macierz) A = diag(1, 2, 1). Wówczas mA(x) = …………….
Odp: Istnieje? (T/N) X = …..

Wówczas: dim ker α = …………. oraz dim im α = ……….
|
Czy (wymierny) układ równań którego macierzą rozszerzoną jest macierz z zadania 6 jest niesprzeczny? Odp: (T/N) ……. . Jeśli jest niesprzeczny to podać też wymiar jego zbioru rozwiązań. Odp: dim = ……..
Wówczas: mSS(α) = ……..
Odp:
mA = ……………………
iA = ……………………..
pJord = ………………….
Zestaw 4
|
Niech ![]()
będzie taka, że chA(x) = x3 + x - 1. Wskazać wielomian w ∈ Q[x] taki, że deg w ≤ 2 oraz w(A) = A-1. Odp: w(x) = …..
|
Niech L = {(x, y)∈R3: x + y = 3}. Zbiór L nie jest podprzestrzenią wektorową R2 bowiem ………………………………………………………………………
Odp: Istnieje? (T/N) X = …..

Wówczas: dim ker α = …………. oraz dim im α = ……….
|
Czy (wymierny) układ równań którego macierzą rozszerzoną jest macierz z zadania 6 jest niesprzeczny? Odp: (T/N) ……. . Jeśli jest niesprzeczny to podać też wymiar jego zbioru rozwiązań. Odp: dim = ……..
Wówczas: mSS(α) = ……..
Odp:
mA = ……………………
iA = ……………………..
pJord = ………………….
8